Введение
В настоящее время улично-дорожные сети крупных российских городов функционируют в условиях повышенной загрузки. Для многих городских улиц характерным становится возникновение систематических транспортных заторов. Используемая в отечественной и зарубежной практике методика расчета режимов работы светофорных объектов определяет длительность светофорного цикла С по следующей формуле:
; (1)
где Tп – суммарное потерянное время за цикл. с; Y – суммарный фазовый коэффициент 
; N – множество фаз регулирования на пересечении; j – группа полос движения, 
; J – множество смежных полос, движение по которым регулируется отдельными сигналами светофоров; 
– интенсивность движения в i фазе по j полосе движения, авт./ч; 
– поток насыщения по j полосе движения, авт./ч.
Полученная длительность светофорного цикла распределяется между фазами пропорционально критическим фазовым коэффициентам:
; (2)
где 
– длительность i фазы регулирования.
Очевидно, что при достаточно высокой интенсивности движения vi,j устанавливается недопустимое значение знаменателя формулы (1):
.
С учетом приведенного выше можно констатировать, что разработка методики расчета режимов работы светофорных объектов в условиях насыщенного движения является одной из актуальных задач управления транспортными системами городов.
Постановка задачи оптимизации работы светофорного объекта
Процесс управления предполагает наличие цели, к достижению которой направлено функционирование систем управления. При этом под качеством функционирования (критерием эффективности) системы управления будем понимать степень ее приспособленности к выполнению стоящей перед ней задачи – обеспечение безопасного пропуска транспортных средств с минимальными задержками. Соответственно задачу оптимального управления изолированным светофорным объектом можно записать следующим образом:
, (3)
при ограничениях
; (4)
; (5)
где 
– функция средней задержки транспортных средств; – длительность разрешающего сигнала в i фазе, с; 
и 
– соответственно минимальная и максимальная длительность разрешающего сигнала, с; 
– положение фронта очереди, авт.; 
– средняя длина автомобиля, м; 
– длина группы полос движения j, м.
Введение ограничения на длину очереди (5) связано с образованием остаточной очереди в цикле регулирования в условиях насыщенного движения [3; 4].
Функция 
должна обеспечивать вычисление задержки как в условиях свободного, так и насыщенного движения. Воспользуемся моделью задержки, приведенной в Highway Capacity Manual [5]. Модель задержки включает три слагаемых:
.
где d1 – постоянная составляющая задержки, с/авт.; PF – фактор прогрессии; d2 – случайная задержка, с/авт.; d3 – задержка перенасыщения, с/авт.
Постоянная составляющая задержки вычисляется как:
,
где X – степень насыщенности группы полос движения (v/c); c – пропускная способность группы полос движения 
, авт./ч.
Случайная задержка определялась с учетом нестационарности процесса формирования очереди:
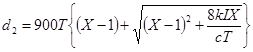, (6)
где T – продолжительность периода анализа в часах; k – коэффициент корректировки, учитывающий способ управления (для предрассчитанного управления принимается равным 0,50); I – коэффициент корректировки, учитывающий влияние соседних перекрестков (для изолированных регулируемых пересечений равен 1.0).
Задержка перенасыщения определяется величиной остаточной очереди на анализируемом периоде Т по формуле:
; (7)
;
;
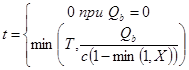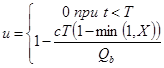где 
– величина остаточной очереди, авт.; t – продолжительность неудовлетворения спроса, ч.
Постоянная составляющая задержки d1 в период наличия остаточной очереди будет вычисляться при X=1.0, для периода (T-t) отсутствия остаточной очереди будет использоваться актуальное значение X:
. (8)
Положение фронта очереди 
ограничения (5) в Highway Capacity Manual определяется формулой:
; (9)
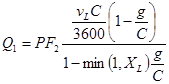; (10)
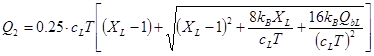; (11)
где vL – интенсивность движения по полосе движения, авт./ч; sL – поток насыщения по полосе движения, авт./ч; cL – поток по полосе движения, авт./ч; QbL – остаточная очередь по полосе движения, авт.; XL – загруженность полосы движения 
; 
– коэффициент прогрессии; kB – коэффициент, связанный с сокращением времени прибытия к фронту очереди.
Как видим, поставленная задача оптимизации работы светофорного объекта (3–5) с учетом выражений (6-8) и (9-11) является задачей нелинейного целочисленного программирования с ограничениями как линейного (4), так и нелинейного (5) вида. Введем функцию штрафа:
, (12)
где inf – достаточно большое число, эквивалентное бесконечности.
Модифицируем задачу (3-5) путем введения функции штрафа (12) в целевую функцию:
. (13)
Алгоритм решения задачи оптимизации работы светофорного объекта
Для решения поставленной задачи могут быть использованы численные методы оптимизации, такие как эволюционные алгоритмы, метод роя частиц, имитация отжига и др., при этом наиболее широкое применение при расчете режимов работы светофорных объектов получили генетические алгоритмы [1; 2].
При расчете режимов работы изолированного светофорного объекта размер области возможных решений P определен количеством фаз регулирования N и размахом возможных значений длительности разрешающих сигналов:
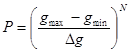, (14)
где 
– шаг приращения длительности разрешающих сигналов, с.
На практике схемы движения с числом фаз регулирования N более 4 не используются, а длительность разрешающего сигнала по условиям безопасности определена на диапазоне значений 
с. С учетом указанных особенностей области возможных решений целесообразно решение задачи (13) методом перебора по сетке возможных решений с шагом .
Существенно сократить количество вычислений можно путем использования итерационной процедуры поиска оптимального решения с переменным шагом :
1) установить начальные значения 
, 
, 
;
2) сгенерировать сетку решений SolveGrid по каждой фазе в диапазоне значений с шагом 
;
3) для каждого узла решения из SolveGrid по формуле (13) вычислить значение целевой функции;
4) решение 
, имеющее минимальное значение целевой функции, является оптимальным;
5) модифицировать начальные значения 
, 
, 
;
6) выполнить пункты 2 – 4.
Количество вычислений целевой функции при использовании метода перебора по сетке возможных решений с постоянным шагом и при использовании итерационного перебора с переменным шагом приведено на рисунке 1.
Для оценки эффективности предложенного алгоритма составлена программа, выполняющая расчеты режимов работы светофорного объекта по приведенной выше методике на языке программирования Python 2.7.
В результате выполнения программы получено совпадение решения, при этом время решения задачи для двухфазной схемы разъезда при использовании метода перебора по сетке возможных решений с постоянным шагом составило 0,757 с, а при использовании итерационного перебора с переменным шагом – 0,044 с.
Тестирование производилось на персональном компьютере с процессором Intel Core i3 и 4,00 Гб оперативной памяти под управлением операционной системы Windows 7.
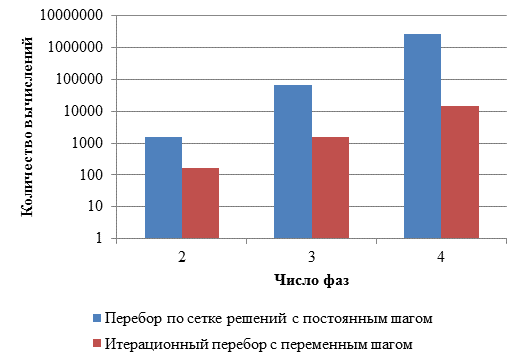
Рисунок 1. Количество вычислений целевой функции
Заключение
В условиях насыщенного движения задача расчёта режимов работы светофорных объектов может быть сформулирована как задача минимизации задержки движения с ограничениями на длину очереди. Для ее решения, в том числе в режиме реального времени, целесообразно использование предложенного алгоритма итерационного перебора по сетке решений с переменным шагом.
Рецензенты:
Родионов Ю.В., д.т.н., профессор кафедры «Эксплуатация автомобильного транспорта» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г.Пенза.
Бажанов А.П., д.т.н., профессор кафедры «Геотехника и дорожное строительство» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Библиографическая ссылка
Власов А.А., Орлов Н.А., Портов Д.В., Скрипкин П.Б. РАСЧЕТ РЕЖИМОВ РАБОТЫ СВЕТОФОРНОГО ОБЪЕКТА В УСЛОВИЯХ НАСЫЩЕННОГО ДВИЖЕНИЯ // Современные проблемы науки и образования. – 2014. – № 3. ;URL: https://science-education.ru/ru/article/view?id=13145 (дата обращения: 14.09.2024).