Введение
По мере увеличения популярности систем видеонаблюдения отмечена тенденция к увеличению площади и геометрической сложности контролируемых территорий. Немалую роль в этом процессе сыграло бурное развитие электронно-вычислительной техники, наблюдаемое в течение последнего десятилетия и которое продолжается и в настоящее время. Развитие средств кодирования, передачи, хранения и отображения видеоинформации привело к быстрому росту числа видеопотоков, поступающих от регистрирующих устройств в центры анализа данных. Традиционно вся работа по оценке ситуации на контролируемой территории отводится оператору – наблюдателю, визуально оценивающему поступающую видеоинформацию. Это физически и психологически сложная работа, требующая постоянной сосредоточенности на однообразной информации, и как следствие приводящая к быстрой утомляемости и снижению качества анализа [1].
Наблюдаемая сегодня интеллектуализация средств видеонаблюдения – создание и внедрение технологий компьютерного анализа, выполняющих часть функций оператора, направлена на преодоление приведенных выше сложностей и должна существенно расширить круг решаемых задач. В идеальном случае оператор может выступать в роли эксперта, которому предъявляются изображения от камер наблюдения, видеоряд которых был предварительно классифицирован в автоматическом режиме как представляющий определенный интерес. Это позволит существенно увеличить количество обрабатываемой одним оператором видеоинформации, а актуальность такого подхода подтверждается увеличением количества работ, посвященных созданию методов автоматического анализа видеоданных – методов видеоаналитики.
Выделение последовательности видеокадров, к которой необходимо привлечь внимание оператора, осуществляется, как правило, на основе анализа траекторий и скоростных режимов движущихся объектов. Таким образом, в последовательности видеокадров производится поиск подвижных объектов, характеристики движения которых не укладывающегося в норму. Однако норма определяется для вида движущегося объекта, так, например, разрешенные направления и скорости движения пешеходов и транспортных средств на пешеходном переходе будут существенно различаться.
В данной работе излагается метод разделения подвижных объектов на классы:
-
автомобилей;
-
пешеходов;
-
неопознанных объектов.
Классификация контуров подвижных объектов
Задача классификации подвижных объектов на основе анализа формы их контуров, является актуальной в связи с тем, что опирается на данные от видеоаналитических алгоритмов, выполняющихся на более ранних этапах обработки видеоизображений [4]. Это значит, что контур движущегося объекта доступен сразу после поиска на изображении области движения.
Контур объекта – это замкнутая граница вокруг подвижного объекта, которую можно представить в виде упорядоченной последовательности координатных пар:
![]() ; (1а)
; (1а)
![]() , (1б)
, (1б)
где:
![]() – сам контур объекта;
– сам контур объекта;
![]() – точки (в случае работы с изображениями и видео – пиксели) контура;
– точки (в случае работы с изображениями и видео – пиксели) контура;
![]() – общее число точек, составляющих контур;
– общее число точек, составляющих контур;
![]() – координатная пара;
– координатная пара;
![]() – координаты точки на границе контура. [3]
– координаты точки на границе контура. [3]
Приведенное выше представление контура является двумерным, то есть каждый пиксель описывается парой значений. Чтобы сделать представление контура одномерным, необходимо использовать массив центромассных расстояний.
Массив центромассных расстояний – одномерная дискретная упорядоченная последовательность, каждый член которой равен расстоянию от центра масс контура до точки на его границе. Введем обозначение этой последовательности:
![]() , (1в)
, (1в)
где:
![]() – массив центромассных расстояний;
– массив центромассных расстояний;
![]() – расстояние от центра масс до точки на границе контура;
– расстояние от центра масс до точки на границе контура;
![]() – общее число точек, составляющих контур.
– общее число точек, составляющих контур.
Расстояние от центра масс до точки на границе контура может быть вычислено с помощью выражения:
![]() , (2)
, (2)
где:
![]() – расстояние от центра масс до точки на границе контура;
– расстояние от центра масс до точки на границе контура;
![]() – координаты центра масс;
– координаты центра масс;
![]() – координаты точки на границе контура.
– координаты точки на границе контура.
Вычисление массива центромассных расстояний начинается с левой верхней точки контура и производится путем его последовательного обхода по часовой стрелке. На рисунке 1 приведено изображение исходного контура и графическое представление соответствующей ему последовательности центромассных расстояний.
а)  б)
б) 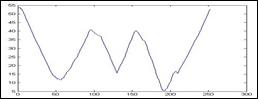
рис. 1. а) Контур изображения; б) центромассные расстояния
На оси абсцисс размещены порядковые номера последовательности точек контура, а на оси ординат соответствующие им расстояния до центра масс.
Описание контуров. Дескрипторы
В теории распознавания образов активно используется понятие дескриптора, которое обозначает уникальную одномерную дискретную упорядоченную последовательность чисел, вычисляемую на основе каких либо свойств объекта. Одним из главных требований к дескриптору является его инвариантность к изменениям свойств объекта, не связанных с его узнаваемостью. Дескриптор контура должен быть инвариантен относительно:
-
поворота;
-
изменения масштаба;
-
параллельного переноса.
Последовательность центромассных расстояний не обладает инвариантностью ни к одному из приведенных выше изменений, кроме параллельного переноса, поэтому не может быть использована в качестве дескриптора. В связи с этим требуется осуществить вычисление дескриптора на основе выбранной формы представления контура.
Обозначим дескриптор как:
![]() , (3)
, (3)
где:
![]() – дескриптор;
– дескриптор;
![]() – одно из чисел образующих дескриптор;
– одно из чисел образующих дескриптор;
![]() – количество чисел в дескрипторе.
– количество чисел в дескрипторе.
Как проиллюстрировано на рисунке 2, с течением времени контур одного и того же объекта может существенно меняться. Особенно изменениям подвержены контуры биологических объектов, которые обладают свойством эластичности. Контуры транспортных средств также могут претерпевать существенные изменения в течение времени, что обусловлено сменой его ракурса по отношению к камере видеонаблюдения.

рис. 2. Изменение внешнего вида контура объекта с течением времени
В связи с этим тип объекта не может быть задан единственным дескриптором, а требуется множество, обладающее полнотой описания по отношению ко всем возможным вариантам, которые могут встретиться в реальном мире. Такое множество дескрипторов будем называть сигнатурой и обозначим как:
![]() , (4)
, (4)
где:
![]() – сигнатура дескрипторных массивов;
– сигнатура дескрипторных массивов;
![]() – дескриптор;
– дескриптор;
![]() – общее количество дескрипторов, каждый из которых описывает объект в определенной позиции.
– общее количество дескрипторов, каждый из которых описывает объект в определенной позиции.
Следует отметить, что инвариантность дескриптора по отношению к повороту, масштабу и сдвигу контура позволяет существенно снизить размеры сигнатур.
Для достижения инвариантности массива центромассных расстояний к повороту и масштабированию необходимо провести Фурье-преобразование данных центромассных расстояний ![]() . Количество Фурье-коэффициентов
. Количество Фурье-коэффициентов ![]() . Будем вычислять отдельно действительную и мнимую части Фурье-преобразования, затем найдем амплитудный спектр, который будет:
. Будем вычислять отдельно действительную и мнимую части Фурье-преобразования, затем найдем амплитудный спектр, который будет:
-
инвариантен к повороту контура;
-
инвариантен к масштабированию контура.
Начинается вычисление Фурье-коэффициентов с коэффициентов нулевой гармоники:
![]() ; (5а)
; (5а)
![]() , (5б)
, (5б)
где:
![]() – действительная и мнимая части Фурье-преобразования;
– действительная и мнимая части Фурье-преобразования;
![]() – расстояние от центра масс до точки на границе контура;
– расстояние от центра масс до точки на границе контура;
![]() – общее число точек, составляющих контур;
– общее число точек, составляющих контур;
Далее вычисляются остальные члены действительной части ![]() , кроме последнего. В данном случае счетчик по коэффициентам
, кроме последнего. В данном случае счетчик по коэффициентам ![]() . Члены действительной части вычисляются по следующей формуле:
. Члены действительной части вычисляются по следующей формуле:
![]() . (6)
. (6)
Затем вычисляется последний член действительной части ![]() :
:
![]() . (7)
. (7)
После находятся оставшиеся члены мнимой части ![]() . В данном случае счетчик по членам мнимой части
. В данном случае счетчик по членам мнимой части ![]() . Мнимая часть вычисляется по формуле:
. Мнимая часть вычисляется по формуле:
![]() . (8)
. (8)
На основе коэффициентов ![]() и
и ![]() вычисляется амплитудный спектр
вычисляется амплитудный спектр ![]() . Счетчик по спектру
. Счетчик по спектру ![]() . Коэффициенты вычисляются по следующей формуле:
. Коэффициенты вычисляются по следующей формуле:
![]() . (9)
. (9)
Затем амплитудный спектр нормируются по нулевой гармонике, и формируется дескриптор контура:
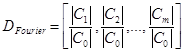 . (10)
. (10)
Этот дескриптор инвариантен к повороту и масштабированию. Кроме того, в зависимости от необходимой точности можно анализировать только первые несколько коэффициентов [2].
Сравнение дескрипторов. Коэффициент корреляции
Решение задачи классификации подвижных объектов лежит в плоскости сравнения дескрипторов наблюдаемых объектов с заранее подготовленными сигнатурами – эталонами. Знание степени соответствия дескриптора классифицируемого объекта каждому из эталонов дает возможность принять решение о его принадлежности к тому или иному классу.
Дескрипторы могут сравниваться с помощью коэффициента корреляции. Вычисляется коэффициент корреляции по следующей формуле:
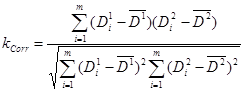 , (11)
, (11)
где:
![]() – коэффициент корреляции;
– коэффициент корреляции;
![]() – члены двух сравниваемых дескрипторов;
– члены двух сравниваемых дескрипторов;
![]() – средние значения среди членов двух сравниваемых дескрипторов;
– средние значения среди членов двух сравниваемых дескрипторов;
![]() – общее количество членов в дескрипторе;
– общее количество членов в дескрипторе;
![]() – счетчик.
– счетчик.
Величина коэффициента корреляции находится в интервале ![]() . Чем больше коэффициент корреляции, тем выше сходство двух сравниваемых дескрипторных массивов.
. Чем больше коэффициент корреляции, тем выше сходство двух сравниваемых дескрипторных массивов.
Коэффициент корреляции можно изменить следующим образом:
![]() , (11а)
, (11а)
где:
![]() – модифицированный коэффициент корреляции.
– модифицированный коэффициент корреляции.
Величина модифицированного коэффициента корреляции находится на интервале ![]() . Чем меньше модифицированный коэффициент корреляции, тем выше сходство двух сравниваемых дескрипторов.
. Чем меньше модифицированный коэффициент корреляции, тем выше сходство двух сравниваемых дескрипторов.
Сравнение дескрипторов. Евклидово расстояние
Евклидово расстояние между дескрипторами может быть вычислено на основе следующего выражения:
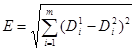 , (12)
, (12)
где:
![]() – Евклидово расстояние;
– Евклидово расстояние;
![]() – члены двух сравниваемых дескрипторов;
– члены двух сравниваемых дескрипторов;
![]() – общее количество членов в дескрипторе;
– общее количество членов в дескрипторе;
Величина Евклидова расстояния находится в промежутке ![]() . Чем меньше Евклидово расстояние, тем выше сходство двух сравниваемых дескрипторных массивов.
. Чем меньше Евклидово расстояние, тем выше сходство двух сравниваемых дескрипторных массивов.
Сравнение дескрипторов. Лямбда расстояние
Лямбда-расстояние учитывает нормированное расстояние ![]() между дескрипторами (
между дескрипторами (![]() – Евклидово расстояние, рассмотренное ранее) и характеристику локальной плотности –
– Евклидово расстояние, рассмотренное ранее) и характеристику локальной плотности – ![]() .
.
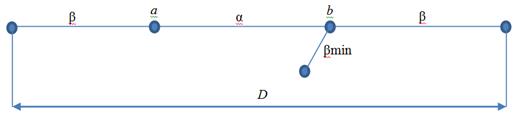
рис. 3. Граф Евклидовых расстояний дескрипторных массивов
Если определить расстояния между всеми парами точек множества ![]() (за точку считаем дескрипторный массив, описывающий определенный контур объекта), то можно построить полный граф, соединяющий все точки со всеми. В этом графе существует самое длинное ребро – диаметр графа, которое обозначим за
(за точку считаем дескрипторный массив, описывающий определенный контур объекта), то можно построить полный граф, соединяющий все точки со всеми. В этом графе существует самое длинное ребро – диаметр графа, которое обозначим за ![]() . Если выделить две любые произвольные точки
. Если выделить две любые произвольные точки ![]() и
и ![]() , то может быть найдена длина связывающего их ребра
, то может быть найдена длина связывающего их ребра ![]() , а также ее нормированная величина:
, а также ее нормированная величина:
![]() . (13)
. (13)
Среди ребер, смежных ребру ![]() , может быть найдено самое короткое, длину которого обозначим за
, может быть найдено самое короткое, длину которого обозначим за ![]() . Отношение длин этих смежных отрезков может быть вычислено на основе выражения:
. Отношение длин этих смежных отрезков может быть вычислено на основе выражения:
![]() . (14)
. (14)
Чтобы сделать эту величину нормированной в диапазоне от нуля до единицы, найдем в полном графе наибольшее значение ![]() , тогда величина:
, тогда величина:
![]() (15)
(15)
является нормированной характеристикой локальной неоднородности плотности множества в окрестностях точек ![]() и
и ![]() . Величину:
. Величину:
![]() (16)
(16)
называют лямбда-расстоянием между точками ![]() и
и ![]() . Параметр
. Параметр ![]() играет более важную роль по сравнению с параметром
играет более важную роль по сравнению с параметром ![]() , поэтому в качестве меры расстояния используется величина:
, поэтому в качестве меры расстояния используется величина:
![]() . (17)
. (17)
По аналогии с Евклидовым расстоянием или модифицированным коэффициентом корреляции выбирается наименьшее лямбда-расстояние, так как оно соответствует более схожим дескрипторам [5].
Пороговые условия
Для пар дескрипторов, на основе введенных выше мер близости определим способ перехода к бинарному показателю соответствия.
Для решения этой задачи введем пороговое условие, которое задается выражением:
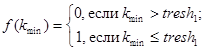 (18)
(18)
где:
![]() – мера близости дескрипторов, в качестве которой выступает модифицированный коэффициент корреляции или лямбда-расстояние;
– мера близости дескрипторов, в качестве которой выступает модифицированный коэффициент корреляции или лямбда-расстояние;
![]() ‑ граница первого порогового условия, которая определяет строгость соответствия.
‑ граница первого порогового условия, которая определяет строгость соответствия.
Выражение обращается в ноль, если фиксируется несоответствие пары дескрипторов, в то время как соответствие обращает его в единицу. Необходимость ввода пороговой границы обусловлена тем, что на практике не может быть получено строгое соответствие.
Очевидно, что допустима ситуация, когда среди всего множества эталонных дескрипторов, не найдется ни одного, обращающего выражение 18 в единицу. Поэтому целесообразно ввести новый класс объектов – «нераспознанный».
Необходимость ввода нового вида объекта также продиктована не нулевой вероятностью соответствия классифицируемого объекта сигнатурам двух разных классов объектов. Пример представлен на рисунке 4.
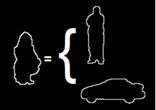
рис. 4. Второй вид ошибок классификации
Ошибка заключается в том, что контур может одинаково походить как на автомобиль, так и на человека. Чтобы исключить ошибки подобного рода, введем второе пороговое условие:
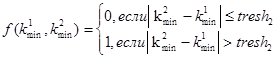 , (19)
, (19)
где:
![]() – мера близости дескрипторов, в качестве которой выступает модифицированный коэффициент корреляции или лямбда-расстояние одного класса;
– мера близости дескрипторов, в качестве которой выступает модифицированный коэффициент корреляции или лямбда-расстояние одного класса;
![]() – мера близости дескрипторов, в качестве которой выступает модифицированный коэффициент корреляции или лямбда-расстояние другого класса;
– мера близости дескрипторов, в качестве которой выступает модифицированный коэффициент корреляции или лямбда-расстояние другого класса;
![]() – граница второго порогового условия.
– граница второго порогового условия.
Второе пороговое условие сравнивает два минимальных значения модифицированных коэффициентов корреляции или лямбда-расстояний. Каждое минимальное значение отвечает за сигнатуру эталонов, принадлежащую своему классу. То есть, если ![]() – это минимум среди эталонов людей, то
– это минимум среди эталонов людей, то ![]() – минимум среди эталонов машин. Разность этих минимумов по модулю должна быть выше определенного порога.
– минимум среди эталонов машин. Разность этих минимумов по модулю должна быть выше определенного порога.
Принадлежность классифицируемого объекта двум классам обусловлена тем, что множества дескрипторов двух сигнатур пересекаются. Такое пересечение связанно с тем, что существуют ракурсы, при которых контуры транспортных средств и пешеходов схожи.
Введение пороговых условий позволяет избежать некоторых ошибок классификации. Если хотя бы одно из пороговых условий не будет выполняться, то контур следует считать неклассифицированным.
Заключение
Исследование методов классификации подвижных объектов на основе контурного анализа показало, что дескрипторы контуров, получаемые с помощью амплитудного спектра преобразования Фурье инвариантны к повороту, масштабированию и параллельному переносу контура изображения. Эти свойства позволяет существенно сократить размеры сигнатур классифицируемых объектов. Также исследование мер близости дескрипторов: корреляционного метода и метода сравнения дескрипторов по лямбда-расстоянию позволило разработать логические решающие правила, которые позволяют избежать ошибок, возникающих при неправильной или неуверенной классификации подвижных объектов.
Рецензенты:
Берестнева О.Г., д.т.н., профессор, кафедра прикладной математики, Томский политехнический университет, г. Томск.
Кочегуров В.А., д.т.н., профессор, кафедра прикладной математики, Томский политехнический университет, г. Томск.
Библиографическая ссылка
Макаров М.А. КОНТУРНЫЙ АНАЛИЗ В РЕШЕНИИ ЗАДАЧ ОПИСАНИЯ И КЛАССИФИКАЦИИ ОБЪЕКТОВ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13130 (дата обращения: 11.02.2026).



