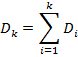Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гергет О.М. 1 Кочегуров В.А. 1 Титаренко Е.Ю. 1

---

1 Национальный исследовательский Томский политехнический университет

Статья является результатом научных исследований сотрудников кафедры прикладной математики Томского политехнического университета, работающих в коллективе научной школы «Разработка физических основ программного обеспечения энерго-информационного представления функциональных особенностей организма в задачах лечебно-профилактической медицины», и посвящена вопросам разработки универсального математического аппарата, который позволит решать задачи контроля, адаптации и управления. В статье с позиции системного подхода рассматривается процесс взаимодействия макрооорганизма с внешней средой. Изложены основные методы классификации объекта исследования (организм человека) на однородные группы. Особое внимание уделено классификации объектов по группам в пространстве главных компонент. Приведен пример работы алгоритма на реальных данных. Представлен критерий оценки адаптационных возможностей организма человека.

Статья в формате PDF

168 KB

адаптация

макросистема

типология

математическое моделирование

1. Агаджанян Н.А. Физиологические и социальные аспекты адаптации человека к экстремальным условиям // Узлов. вопр. совр. физиол. — Томск, 1984. — С. 47-63.

2. Баевский Р.М. Прогнозирование состояний на грани нормы и патологии. — М., 1979. — 196 с.

3. Гергет О.М., Кривоногова Т.С. Математические методы оценки влияния комплекса реабилитационных мероприятий в охране здоровья матерей и их детей // Вопросы современной педиатрии. — 2009. - № 5. — С. 15-23.

4. Князева Е.Н., Курдюмов С.П. Законы эволюции и самоорганизации сложных систем. — М. : Наука, 1994. — 229 с.

5. Кобринский Б.А., Фельдман А.Е. Анализ и учет ассоциативных знаний в медицинских экспертных системах // Новости искусственного интеллекта. — 1995. - № 3. — С. 90-96.

6. Кочегуров В.А., Гергет О.М., Константинова Л.И. Модели закономерностей развития детей в раннем периоде и методы оценки их состояния // Проблемы информатики. — 2012. — № 5 (17). — С. 6-12.

Введение

В последнее время проблема здоровья населения привлекает внимание все большего числа исследователей в разных областях, что связано со значительным ухудшением здоровья всего населения. При этом наиболее продуктивным считается адаптационный подход к изучению здоровья [1; 2; 4; 5]. Особенности и трудности изучения адаптационного процесса связаны с тем, что в процессе формирования адаптации человек ставит две цели – приспособиться к условиям внешней среды, например к высокой или низкой температуре, недостатку кислорода, особенностям питания и т.п., и одновременно приспособиться к деятельности, особенно трудовой и социальной, при наличии таких природных условий. Наиболее сложная ситуация возникает в тех случаях, когда требования обеспечения деятельности не совпадают с требованиями сохранения гомеостата при действии внешнего фактора. Современное состояние исследований и разработок в данной области отражено во множестве научных публикаций. Однако до сих пор существует необходимость поиска новых подходов к оценке и исследованию адаптационных процессов как взрослых, так и детей.

Методы исследования

Изучение процессов адаптации здорового человека сводится к исследованию процесса взаимодействия организма человека с внешней средой. Схематично это взаимодействие может быть представлено структурной схемой (рис. 1).

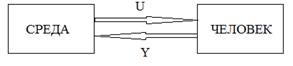
Рис. 1. Структурная схема объекта исследования

U – параметры внешней среды, воздействующие на человека;

Y – показатели, характеризующие взаимодействие человека со средой.

Организм человека рассматривается в целом во взаимодействии его отдельных систем и внешней среды. Важно правильно определить перечень параметров, характеризующих внешнюю среду, и перечень показателей организма человека, наиболее чувствительных к изменениям выбранных параметров внешней среды.

Поскольку объектом исследования является человек, это создает определенные трудности в использовании хорошо разработанных в теории управления методов идентификации сложных технических систем для построения организменных моделей. Одна из главных трудностей заключается в получении объективных и независимых измерений параметров организма, необходимых для моделирования. Это связано с тем, что на временные характеристики состояния организма одного человека оказывает влияние сам процесс измерения (например, для биохимического анализа крови через небольшие промежутки времени). В связи с этим ставится задача выделения однородной группы людей, близких по выбранным показателям, с тем, чтобы нужные показатели для построения модели снимать не с одного и того же человека, а получать их от разных людей из принятой однородной группы и строить усредненную модель некоторого «макроорганизма». На этом этапе возникает важная проблема классификации людей по однородным группам, выбора признаков, объектов классификации и их измерения.

После классификации людей на однородные группы, выбора параметров внешней среды и показателей организма человека выбирается модель взаимодействия организма человека с внешней средой, и устанавливаются требования к проведению эксперимента по оцениванию параметров принятой модели. Далее производится проверка адекватной полученной групповой модели взаимодействия «макроорганизма» с внешней средой. Это можно сделать на основании машинного моделирования внешней среды и ее влияния на объективные показатели состояния организма.

Классификация людей на однородные группы

Задача классификации относится к задачам типологии, т.е. требуется разделить множество наблюдаемых объектов (людей), описанных некоторым набором признаков, на сравнительно небольшое число областей с тем, чтобы элементы одной такой области лежали по возможности на небольшом расстоянии друг от друга. Таким образом, имеем n объектов (людей) , каждый объект представляет собой вектор в m-мерном пространстве изображений, координаты которого несут количественную информацию об объекте, т.е.

, .

В качестве признаков, характеризующих объект, предварительно были выбраны признаки, которые можно разделить на следующие группы [3]:

• анкетные данные;
• объективные показатели;
• анамнестические данные;
• признаки, отвечающие за усредненные созданные изменения организма.

Поскольку организм человека подвергается сезонным колебаниям, то при классификации людей необходимо добавить показатели организма, имеющие сезонную ритмичность [3].

Задача типологии (таксономии) может решаться непосредственно с помощью методов автоматической классификации.

Но в многомерных случаях решение задач классификации предусматривает в качестве предварительного этапа исследования реализацию методов, позволяющих существенно сократить размерность исходного факторного пространства. Одним из таких методов является метод главных компонент.

Главные компоненты представляют собой новое множество исследуемых признаков V¹, V², ..., V^m, каждый из которых получен в результате некоторой линейной комбинации непосредственно измеренных на объектах исходных признаков

, (1)

.

Геометрически метод главных компонент представляет собой переход к новой системе координат. При этом используется понятие об эллипсоидах (обычно облако точек, представляющих n объектов в m-мерном пространстве, имеет форму более или менее близкую к эллипсоиду и становится в точности эллипсоидом в случае нормального распределения). Есть смысл в качестве системы координат взять главные оси эллипсоида. Если в качестве факторов взять главные оси эллипсоида, то на первый фактор приходится максимально возможная доля суммарной дисперсии, второй фактор учитывает максимум дисперсий в пространстве, которое получится после исключения первого фактора, и т.д.

Анализируя изменение относительной доли дисперсии по формуле:

вносимой первыми P главными компонентами, в зависимости от числа этих компонент, можно определить число компонент, которое целесообразно оставить в рассмотрении.

После нахождения значений [6] в отражении (1) можно составить окончательные уравнения для главных компонент, и по вкладу каждого фактора z в суммарную дисперсию (сумма дисперсий в процентах дает 100%) можно определить наиболее существенные исходные факторы (табл. 1).

Таблица 1

В правом столбце таблицы подсчитан вклад каждого фактора в процентах в суммарную дисперсию. Откуда видно, что никакими из этих признаков нельзя пренебречь.

Классификация объектов по группам проводится в пространстве главных компонент. Для классификации используются дисперсионный метод самопроизвольного разбиения пространства изображений на компактные множества. Этот метод позволяет заменить разбиение в многомерном пространстве описаний разбиением в одномерном пространстве проекций изображений в направлении главного, собственного вектора, т.е. в направлении первой главной компоненты. В качестве разделяющих точек принимаются значения минимумов выборочной функции плотности точек проекций на этой оси. Эти точки находятся методом оптимальной дихотомии. Критерием достаточности разбиения принято смещение дисперсий после очередной дихотомии, но не более 0,5. В результате разбиения получили табл. 2 [6].

Таблица 2

Выбор модели

Имея вместо отдельного организма некоторую однородную группу – макроорганизм, можно описать процесс взаимодействия макрооорганизма с внешней средой функциональной зависимостью, которая в общем виде определяется через нелинейные уравнения состояния.

Пусть – переменные внешней среды, воздействующие на макроорганизм; – контролируемые переменные, характеризующие реакцию макроорганизма на внешнюю среду и определяющие состояние отдельных систем;
– переменные, описывающие состояние макросистемы.

Связь между описанными переменными может быть представлена в следующем виде:

(2)

(3)

Введем средние значения переменных, характеризующих состояние макроорганизма для выбранной группы людей и внешней среды через на определенном интервале времени. Состояние макроорганизма в заданном интервале времени в точке назовем равновесным. Колебания внешней среды вблизи вызывают соответствующие отклонения переменных x и y . Функции (2), (3) разложим в ряд Тейлора вблизи равновесной точки и ограничимся линейной частью:

где ; ; ; – коэффициенты, характеризующие чувствительность показателей и скорость изменения параметров состояния к колебаниям внешней среды и переменным состояния макроорганизма вблизи точки равновесия.

Значения этих коэффициентов в точке равновесия обозначим следующим образом:

Тогда уравнения (2), (3) можно переписать в виде

(4)

(5)

Уравнения (4), (5) являются уравнениями состояния в векторно-матричной форме и в нашем случае могут рассматриваться в качестве математической модели реакции макроорганизма на изменения внешней среды, линеаризованной вблизи равновесной точки, характеризуемой средними значениями

Структурная схема приведена на рис. 2.

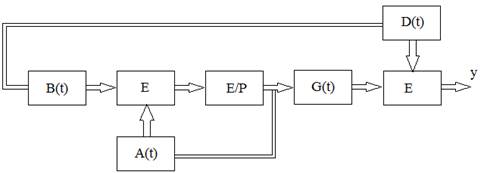
Рис. 2. Структурная схема модели

В векторно-матричной форме модель взаимодействия человека с внешней средой представлена как некоторая замкнутая система, подверженная воздействию внешней среды и обеспечивающая адаптацию (самоорганизацию) к внешней среде через каналы прямой и обратной связи. При колебаниях внешней среды связи остаются неизменными, меняется лишь интенсивность связей.

При этом под адаптацией можно понимать следующее: выходные сигналы Y должны оставаться в заданном интервале ΔY при изменении входных сигналов внешней среды за счет соответствующего изменения коэффициентов матриц.

Вывод

Рассмотренные в статье модели и методы направлены на решение одной из важных проблем: создания эффективных инструментов решения задачи диагностики и оценки процессов адаптации организма человека к изменяющимся условиям внешней среды.

Дальнейшие исследования связаны с разработкой магистральных технологий для выявления закономерности реакции организма на условия жизнедеятельности.

Работа выполнена в рамках проекта № 1957 Госзадания «Наука» Министерства образования и науки Российской Федерации.

Рецензенты:

Силич В.А., д.т.н., профессор, профессор кафедры ОСУ ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.

Мицель А.А., д.т.н., профессор, профессор кафедры АСУ ФГБОУ ВПО «Томский государственный университет систем управления и радиоэлектроники», г. Томск.

Библиографическая ссылка