Введение
Исследования дна Мирового океана, проведенные в начале XXI века [5; 6], свидетельствуют о непрерывных выбросах метана в виде газовых пузырьков. Единичный объем газового гидрата, содержащий в 160 м3 раз больше газа, чем в свободном состоянии [1], позволяет рассматривать гидрат как один из наиболее перспективных источников углеводородного сырья. Добыча гидрата может происходить как в недрах материка [2], так и на дне водоемов. Нередко газовые гидраты создают трудности при добыче углеводородов, и используются специальные средства для предупреждения их образования [3]. Особый интерес для исследователей представляет процесс покрытия газовых пузырьков гидратной коркой, образование которой характерно для всплытия метановых пузырьков. Термобарические условия, соответствующие дну Мирового океана, идеально подходят для процесса гидратообразования, фазовая диаграмма представлена на рис. 1.
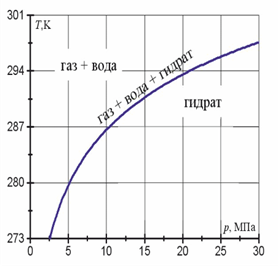
Рис. 1. Диаграмма фазового равновесия метана
Схема процесса накопления гидратных частиц внутри купола представлена на рис. 2. Согласно предлагаемой схеме на дне водоема имеется источник всплытия метановых пузырьков с известным массовым расходом ![]() и купол цилиндрической формы, зафиксированный на некоторой высоте
и купол цилиндрической формы, зафиксированный на некоторой высоте ![]() . Верхняя крышка купола закрыта, нижняя открыта. Таким образом, внутрь купола могут проникать пузырьки метана.
. Верхняя крышка купола закрыта, нижняя открыта. Таким образом, внутрь купола могут проникать пузырьки метана.
Будем полагать, что нижнее основание купола зафиксировано на такой высоте ![]() , что температура окружающей воды
, что температура окружающей воды ![]() ниже равновесной температуры гидратообразования
ниже равновесной температуры гидратообразования ![]() :
:
![]() ,
, ![]() . (1)
. (1)
При этом примем, что при выполнении условия (1) пузырьки газа начинают покрываться газогидратной коркой. Пусть ![]() – число пузырьков в единице объёма. Пусть
– число пузырьков в единице объёма. Пусть ![]() – скорость миграции гидратной частицы,
– скорость миграции гидратной частицы, ![]() – скорость воды, вымещающейся из купола за счет поступающих частиц. Тогда скорость поднятия частиц:
– скорость воды, вымещающейся из купола за счет поступающих частиц. Тогда скорость поднятия частиц: ![]() .
.
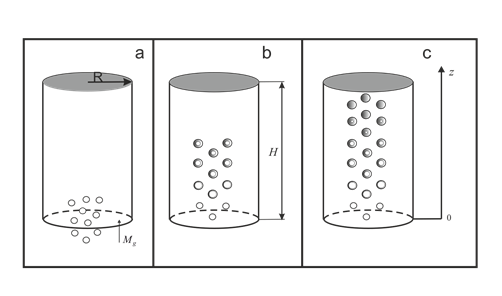
Рис. 2. Схема процесса всплытия метановых пузырьков в куполе-сепараторе. H и R – высота и радиус основания купола, белыми кругляшками обозначены пузырьки газа, серыми – частицы гидрата, частично серыми – пузырьки, покрытые гидратной коркой.
Уравнение сохранения числа пузырьков запишется в виде:
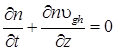 . (2)
. (2)
Уравнения сохранения масс для пузырьков и воды [4]:
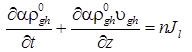 , (3)
, (3)
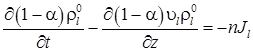 , (4)
, (4)
где ![]() и
и ![]() – интенсивности образования гидрата и расхода воды, идущей на его образование;
– интенсивности образования гидрата и расхода воды, идущей на его образование; ![]() – объемное содержание пузырьков;
– объемное содержание пузырьков; ![]() – средняя плотность газогидратного пузырька, определяемая как отношение всей массы пузырька на его общий объем.
– средняя плотность газогидратного пузырька, определяемая как отношение всей массы пузырька на его общий объем.
Гидрат является клатратным соединением с массовым содержанием газа G, поэтому интенсивность образования гидрата и расхода воды связаны как:
![]() . (5)
. (5)
Приведенные уравнения необходимо дополнить следующим кинематическим соотношением:
![]() , (6)
, (6)
где a – радиус газогидратного пузырька.
Уравнения импульсов для газогидратных пузырьков и для жидкости в безынерционном приближении соответственно могут быть записаны в виде [4]:
![]() (7)
(7)
![]() (8)
(8)
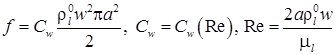 ,
,
где f – сила трения между пузырьком и водой.
Запишем уравнение для изменения температуры жидкости за счет температурного следа пузырьков, возникающего вследствие гидратообразования:
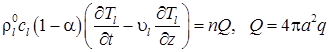 , (9)
, (9)
где ![]() и
и ![]() – температура и теплоемкость воды;
– температура и теплоемкость воды; ![]() и
и ![]() – интенсивности источника тепла из-за гидратообразования, отнесенные на единицу объема и однородного пузырькового включения. Здесь и далее нижние индексы
– интенсивности источника тепла из-за гидратообразования, отнесенные на единицу объема и однородного пузырькового включения. Здесь и далее нижние индексы ![]() относятся к параметрам газа, воды и гидрата.
относятся к параметрам газа, воды и гидрата.
Жидкость будем считать несжимаемой, а газ калорически совершенным:
![]() ,
, ![]()
![]() . (10)
. (10)
Полагаем, что газогидратные пузырьки состоят из газового ядра радиусом ![]() и гидратной «скорлупы». Тогда для средней плотности
и гидратной «скорлупы». Тогда для средней плотности ![]() :
:
![]() , (11)
, (11)
где![]() – истинные плотности газовой и гидратной фаз.
– истинные плотности газовой и гидратной фаз.
Выражение (11) разрешим относительно плотности газогидратного пузырька, которое будет иметь вид:
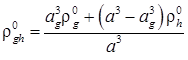 . (12)
. (12)
Следовательно, средняя плотность ![]() газогидратного пузырька определяется значениями радиусов газового ядра
газогидратного пузырька определяется значениями радиусов газового ядра ![]() и всего пузырька а, а также текущей плотностью газа
и всего пузырька а, а также текущей плотностью газа ![]() .
.
В газогидратном пузырьке газ содержится как в свободном состоянии, так и в составе гидрата с массовым содержанием G. Запишем условие постоянства общей массы газа в пузырьке как:
![]() , (13)
, (13)
где ![]() ,
, ![]() – искомые значения радиуса и плотности газа в пузырьке.
– искомые значения радиуса и плотности газа в пузырьке.
Примем, что интенсивность образования гидратного пузырька лимитируется интенсивностью отвода тепла от его поверхности жидкостью:
![]() , (14)
, (14)
где ![]() – удельная теплота образования гидрата.
– удельная теплота образования гидрата.
Расчеты производились для следующих значений: ![]() кг/м3,
кг/м3, ![]() кг/м3,
кг/м3, ![]() Дж/кг,
Дж/кг, ![]() Дж/(м с К),
Дж/(м с К), ![]() Дж/(кг К),
Дж/(кг К), ![]()
![]() Дж/(кг К),
Дж/(кг К), ![]() ,
, ![]() , H =20 м, h= 10 м, R=4 м.
, H =20 м, h= 10 м, R=4 м.
На рис. 3-5 представлены результаты для момента времени, когда гидратные частицы достигли высоты z=14,5 м. На рис. 3-4 представлены зависимости радиуса и плотности частицы от вертикальной координаты. Из рис. 3 видим, что на высоте z=1 м радиус частицы прекращает рост, становится стационарным. Из рис. 4 видим, что пузырьки полностью покрываются гидратной коркой, превращаясь в гидратную частицу на высоте z=1 м.
На рис. 5 представлена зависимость температуры воды в куполе от вертикальной координаты. Температура жидкости внутри купола не превышает температуру гидратообразования, что свидетельствует о том, что гидратная частица не разлагается.
Выводы
В работе рассмотрен процесс всплытия пузырьков метана внутри купола и их превращение в гидратные частицы. При рассмотрении модели было принято, что интенсивность образования гидратного пузырька лимитируется интенсивностью отвода тепла. Получена зависимость радиуса и плотности гидратной частицы от вертикальной координаты, а также профиль изменения температуры жидкости внутри купола.
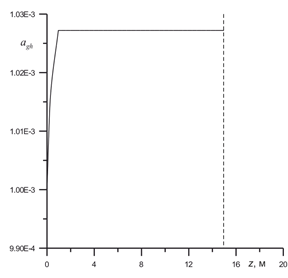
Рис. 3. Зависимость радиуса частицы от вертикальной координаты.
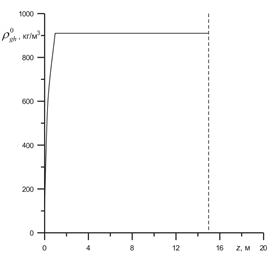
Рис. 4. Зависимость плотности частицы от вертикальной координаты.
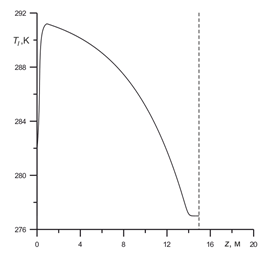
Рис. 5. Зависимость температуры воды в куполе от вертикальной координаты.
Работа выполнена при поддержке гранта СФ БГУ, договор № В14-6.
Рецензенты:
Гималтдинов И.К., д.ф.-м.н., профессор, заведующий кафедрой «Прикладная математика и механика» Стерлитамакского филиала ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.
Мустафина С.А., д.ф.-м.н., профессор, заведующая кафедрой «Математическое моделирование», декан физико-математического факультета Стерлитамакского филиала ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.
Библиографическая ссылка
Кильдибаева С.Р. МОДЕЛИРОВАНИЕ ПРОЦЕССА ВСПЛЫТИЯ ГИДРАТНЫХ ЧАСТИЦ В КУПОЛЕ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=13063 (дата обращения: 11.02.2026).



