В большей части программных пакетов для моделирования инженерных конструкций, основанных на методах конечных элементов, принято следующее допущение. Конечный элемент – малая часть конструкции, имеющая простую форму, моделируется в рамках теории пластин и оболочек. Детали автомобилей можно представить как состоящие из большого количества оболочечных и балочных элементов. Это подтверждено многолетней практикой исследования, проектирования и производства автомобилей.
Чтобы исследовать плотность потока энергии волн в деталях автомобиля, необходимо применить положения теории энергии механических волн к теории метода конечных элементов. И на этой основе моделировать поведение узлов и деталей автомобиля, состоящих из большого множества таких элементов.
Интенсивность волн или плотность потока энергии волны – это величина, равная потоку энергии, переносимой волной через единичную площадь, перпендикулярную направлению распространения волны, измеряется в Ваттах, деленных на квадратный метр. Из работ [1, 2] известно, что плотность потока энергии волны определяется следующими параметрами: плотностью среды, амплитудой, частотой и скорость распространения волны. Чтобы от общих представлений Н.А. Умова перейти к инженерной методике, необходимо на основе теории механических волн и механики сплошных сред описать распространение плотности потока энергии волны в деталях и узлах автомобиля.
Геометрия деталей автомобиля, рассматриваемых в данной работе, аппроксимирована при помощи оболочечных элементов (1-го порядка интерполяции, редуцированной интеграции). Задача решена в статической постановке, с использованием неявного интегрирования метода конечных элементов. При заданных условиях нагружения и закрепления элементы конструкции испытывают продольные и поперечные деформации.
Если прилагаемая нагрузка содержит составляющие в плоскости пластины, то последняя будет одновременно работать и как диафрагма (мембрана), и на изгиб. Так происходит в деталях и узлах рулевого управления автомобилей. Такая комбинация рассматривается в методе конечных элементов в модели плоской оболочки (шелл-элемент).
Если принять допущения: пластина имеет симметричные свойства материала по отношению к срединной плоскости; секции, перпендикулярные к срединной плоскости остаются плоскими в процессе деформации и напряжения, перпендикулярные к пластине небольшие; смещения в плоскости («мембрана») и смещения вне плоскости («изгиб») можно рассматривать как отдельные; только нормальные внешние силы действуют на пластину;
то достаточно рассматривать только изгибное поведение пластины.
Тогда уравнение плотности потока энергии волны во временной области [7, 8]:
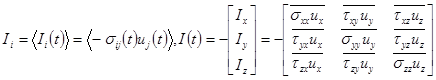, (1)
где 
– интенсивность в направлении i, 
– скорость частицы в направлении j, 
– нормальные и касательные напряжения.
Автор работы [8] полагая, что изменение плотности потока энергии волны в детали для гармонических колебаний можно записать как
, (2)
и, далее подставляя в него выражения для определения 
в направлении i, показал, что в частотной области действительная и мнимая части плотности потока энергии волны связаны с кинетической и потенциальной энергиями следующим образом:
, 
, (3)
где 
и 
– это кинетическая и потенциальная энергия волны в детали; 
– оператор Лапласа, 
и 
– параметры, зависящие от демпфирования (затухания) колебаний и частоты.
Из выражения (3) следует, что:
- действительная часть кросс-спектра плотности потока энергии волны описывает потенциальную энергию и дает представление о распределении стоячих волн [1] в теле детали;
- мнимая часть кросс-спектра плотности потока энергии волны описывает разницу между кинетической и потенциальной энергиями в системе и дает представление о распределении бегущих волн [1] в теле детали.
Если обозначить преобразование Фурье от скорости частицы 
как 
:
, (4)
Тогда, согласно работе [7], выражения для определения плотности потока энергии волны во временной области принимают следующий вид в частотной области (кросс-спектр плотности потока энергии волн):
,
(5)
и комплексные функции 
определяется как:
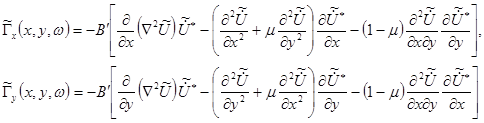(6)
В последних выражениях: знак «*» указывает комплексное сопряжение величины; 
– действительная часть плотности потока энергии волны, полученная преобразованием Фурье мнимой части (6); 
– мнимая часть плотности потока энергии волны, полученная преобразованием Фурье действительной части (6).
Анализируя выражения (3) из работ [5, 6, 8] и выражения (5) из работы [7] , можно сделать следующие выводы.
После перехода из временной области в частотную:
- действительные части выражений (5), обозначенные 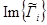, описывают мнимую частью плотности потока энергии волны, т.е. стоячие волны, которые, согласно [2, 3] , не переносят энергию; т.о., при анализе распределения плотности потока энергии волн в деталях автомобилей при помощи этой составляющей можно выявлять места концентрации и рассредоточения энергии механических волн;
- мнимые части выражений (5), обозначенные 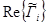, описывают действительную частью плотности потока энергии волны (разницу между кинетической и потенциальной энергиями), т.е. бегущие волны, которые переносят энергию [1, 2]; т.о., при анализе распределения плотности потока энергии волн в деталях автомобилей при помощи этой составляющей можно выявлять пути перемещения энергии механических волн.
Приведенные выше выражения являются математическим описанием физических процессов, происходящих в тонкой оболочке – конечном элементе, на которые разбиваются исследуемые детали рулевого управления автомобилей. И, следовательно, используя такое математическое описание, становится возможным моделировать плотности потоков энергий механических волн в деталях и узлах автомобилей, как для энергии в целом, так для кинетической и потенциальной энергий отдельно.
Чтобы реализовать в практике исследований методику расчета вибрационных параметров автомобиля с учетом плотности потока энергий волн в её деталях, был разработан алгоритм процедуры моделирования (представлен на рисунке 1), который позволил получить поля плотностей потоков потенциальной и кинематической энергий механических волн в деталях рулевой колонки легковых автомобилей.
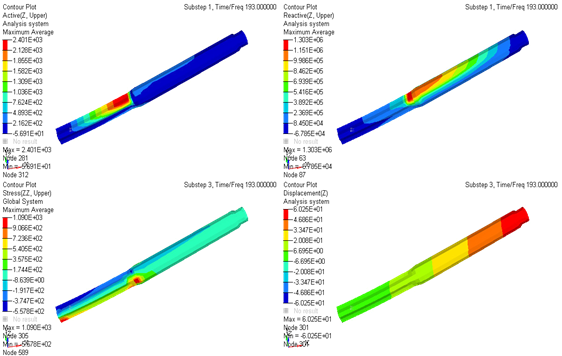
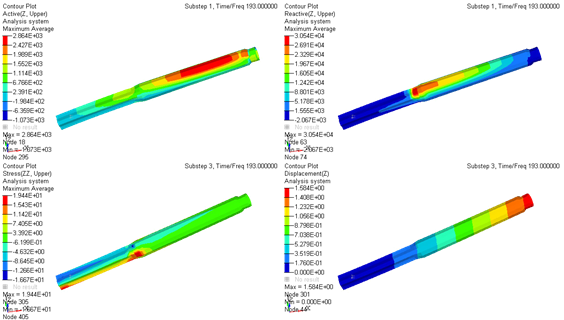
Результаты моделирования плотности потока энергии волн, напряжений и перемещений в верхнем вале рулевой колонки VW PQ35 GP приведены на рис. 2 (максимальные значения величин соответствуют красному цвету, минимальные – синему) [3, 4]. Из приведенных на этом рисунке данных можно заключить:
- распределение перемещений и деформаций в вале рулевой колонки соответствует классическим представлениям – напряжения и перемещения элементов вала убывают от места приложения нагрузки к месту крепления (заделки) (см. второй и четвертый ряды на рис. 2);
- при изменении дэмпфирования качественная картина распределения напряжений и перемещений по телу вала сохраняется, меняются лишь значения напряжений и деформаций (см. второй и четвертый ряды на рис. 2);
- места концентрации потоков вибрационной энергии не соответствуют местам максимальных напряжений и перемещений (сравнение первого и второго, и третьего, и четвертого рядов, соответственно, на рис. 2);
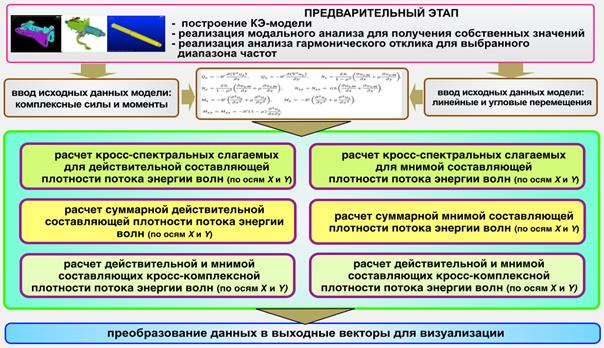
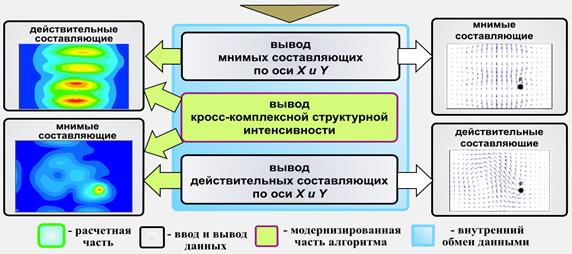
Рис. 1. Алгоритм для моделирования плотности потока энергии механических волн в деталях автомобилей
- поле распространения действительной части потоков вибрационной энергии не меняется при изменении демпфирования в тысячу раз; можно заключить, что эта часть потоков вибрационной энергии описывает поведение стоячих волн и описывает потенциальную энергию в деталях (первый и третий ряд, правый рисунок);
- у мнимой части потоков вибрационной энергии происходит перемещение мест концентрации с изменением демпфирования; можно заключить, что эта часть потоков вибрационной энергии описывает поведение бегущих волн,и описывает перемещение энергии в деталях (первый и третий ряд, левый рисунок);
- при увеличении демпфирования область концентрации действительной части вибрационной энергии увеличивается и перемещается ближе к источнику нагрузки (первый и третий ряд, левый рисунок).
0,0001
0,1
Рис. 2. Моделирование поведения верхнего вала рулевой колонки VW PQ35 GP («Фольксваген») при двух значениях коэффициента демпфирования:
- первый и второй ряды - 0,0001, третий и четвертый ряды - 0,1;
- первый и третий ряды - распределение действительной (активной) части (слева) и мнимой (реактивной) части плотности потока энергии волны;
- второй и четвертый ряды - напряжения (слева) и деформации по оси аппликат
По результатам проведенных исследований [3, 4] было доказано, что векторы плотности потока энергии волны являются идентификаторами вибрационного поведения и позволяют: делать заключения о характере распределения вибрационной энергии в деталях автомобилей, объяснять и описывать появление вибрации в местах, где её источники, согласно традиционному анализу напряжений в деталях, отсутствуют.
Рецензенты:
Беляков В.В., д.т.н., профессор кафедры «Автомобили и тракторы» ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Слюсарев А.С., д.т.н., профессор кафедры «Прикладной механики и подъемно-транспортных машин» ФГБОУ ВПО «Волжская государственная академия водного транспорта», г. Нижний Новгород.
Библиографическая ссылка
Шапкина Ю.В. МОДЕЛИРОВАНИЕ ПЛОТНОСТИ ПОТОКА ЭНЕРГИИ ВОЛН В ДЕТАЛЯХ АВТОМОБИЛЕЙ // Современные проблемы науки и образования. – 2014. – № 2. ;URL: https://science-education.ru/ru/article/view?id=12858 (дата обращения: 04.10.2024).