Введение
Определение координат источника светового излучения обычно осуществляется путем измерения отклонения его изображения в фокальной плоскости от фокуса оптической системы. Турбулентность среды распространения значительно снижает точность определения координат и приводит к тому, что тактико-технические характеристики современных оптических измерительных систем (ОИС) значительно отличаются от потенциально возможных. В настоящее время разработан аппарат фазового сопряжения [4], позволяющий эффективно компенсировать нестационарные возмущения световых пучков при их распространении в возмущенных каналах. Поэтому для повышения точности определения параметров движения объекта оптическими измерительными системами целесообразно объединить задачу пеленгации с задачей компенсации нестационарных искажений принимаемого оптического сигнала.
Целью данной работы является численное исследование метода [4] определения параметров движения объекта при проведении траекторных измерений оптическими системами в турбулентной атмосфере при интенсивных шумах регистрации на основе комплексного применения методов адаптивной оптики и додетекторной квазиоптимальной пространственной обработки пуассоновских оптических полей.
Синтез алгоритма определения угловых скоростей объекта
Проведенный анализ показывает, что в оптическом диапазоне для определения угловых скоростей наиболее приемлемым является метод, основанный на измерении угловых координат с последующим их дифференцированием. Очевидно, что точность определения скорости в этом случае не превышает точности измерения координат. Из этого следует, что применение представленного метода в перспективных ОИС возможно лишь совместно с высокоточными методами измерения угловых координат.
Задача определения угловых скоростей может быть решена АОС фазового сопряжения, когда в результате обработки распределения интенсивности на субапертурах датчика Гартмана проводится восстановление фазового фронта принимаемого оптического поля. В таких АОС формируются управляющие напряжения, пропорциональные распределению фазы принимаемого сигнала по апертуре. Таким образом, на базе систем фазового сопряжения может быть организовано измерение угловых координат фазовым методом, обладающим максимальной потенциальной точностью. Применяя к измеренным таким образом угловым координатам методы численного дифференцирования, можно получить оценки азимутальной и угловой скоростей.
Получение этих оценок будем проводить следующем образом. Учитывая взаимосвязь разности фаз сигнала в разнесенных точках приема и направления его распространения, определяемую выражением
![]() , (1)
, (1)
применим фазовый метод пеленгации. Для этого воспользуемся результатами восстановления фазового фронта АОС и в соответствии с алгоритмом [4] определим угловые координаты объекта. Проводя дифференцирование этих координат с привлечением аппарата численных методов, получим оценки угловых скоростей объекта.
Таким образом, процедура определения оценки угловой скорости предполагает выполнение следующих операций.
1. Восстановление фазового фронта оптического излучения.
2. По результатам восстановления расчет наклонов фазового фронта в двух перпендикулярных плоскостях.
3. Определение азимута и угла места объекта.
4. Получение оценки угловых скоростей путем дифференцирования функции, описывающей эволюцию угловых координат объекта.
Обозначим процедуру получения оценок угловых скоростей оператором O
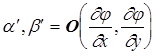 . (2)
. (2)
Тогда предложенный алгоритм в формальном виде запишется образом
![]() . (3)
. (3)
Определение производной функции по времени на практике сводится к отсчету значений функции в некоторые моменты времени и обработке этих отчетов методами численного дифференцирования [4]. При этом максимальное значение интервала времени, через который следует проводить измерения фазы, выбирается с учетом двух взаимосвязанных факторов - времени неоднородности турбулентности и максимальной предполагаемой скорости объекта. Необходимость учета первого фактора обусловлена тем, что адаптивные методы компенсации с воздействием на фазовый фронт оптической волны основываются на свойствах: линейности, взаимности и квазистационарности атмосферы. Для выполнения условий квазистационарности необходимо, чтобы временной отклик оптической системы и время распространения сигнала не превышали времени «замороженности» турбулентной среды, которое составляет 10-3 - 10-2 с. Иными словами, для эффективной компенсации нестационарных искажений необходимо, чтобы принимаемый сигнал, по результатам обработки которого вносятся предыскажения фазы и передаваемый сигнал, распространялись через одни и те же неоднородности. Необходимость учета второго фактора продиктована следующим. Если объект имеет высокую тангенциальную скорость, то при его сопровождении лазерный луч будет направлен в упреждающую точку. Вследствие этого он будут проходить путь, отличающийся от пути, проходимого излучением, принимаемым от объекта. Если же принимаемый и передаваемый лучи будут разнесены более чем на одну поперечную корреляционную длину ![]() , то они будут распространяться через различные воздушные каналы, имеющие статистически независимые характеристики турбулентности. Следовательно, информация о турбулентности, полученная от прошедшего луча не может быть использована для определения величины компенсации турбулентности, воздействующей на передаваемый сигнал.
, то они будут распространяться через различные воздушные каналы, имеющие статистически независимые характеристики турбулентности. Следовательно, информация о турбулентности, полученная от прошедшего луча не может быть использована для определения величины компенсации турбулентности, воздействующей на передаваемый сигнал.
Исследование алгоритмов
Для оценки эффективности синтезированных алгоритмов был проведен вычислительный эксперимент в среде Mathcad.
Точности определения угловых координат адаптивной оптической системой, реализующей алгоритм [1], проводилась в четырех направлениях.
1. Оценивались погрешности определения азимута и угла места предполагаемого объекта при отсутствии шумов регистрации оптического сигнала датчиком фазового фронта.
2. Определялась зависимость погрешности измерения угловых координат предполагаемого объекта от размеров датчика фазового фронта при учете шумов в его каналах.
3. Выяснялся характер зависимости погрешности измерения угловых координат предполагаемого объекта от величины измеряемых углов.
4. Определялась зависимость погрешности измерения угловых координат предполагаемого объекта от величины турбулентности атмосферы при различных уровнях шумов в каналах датчика фазового фронта.
С этой целью искаженный фазовый фронт оптической волны был представлен в виде системы из десяти первых полиномов Цернике [5]. При проведении вычислений ограничились рассмотрением углов наклона фазового фронта от 0 до 10 угловых секунд, что при диаметре апертуры АОС, равном 0,5 метра, и длине волны - 10-6 метра соответствует набегу фазы на апертуре от 0 до 10 длин волн. Выбор такого диапазона измеряемых углов определяется тем, что современные отечественные и зарубежные ОИС способны определять угловые координаты с точностью, равной нескольким угловым секундам, а юстировка датчиков - преобразователей «угол - код» обеспечивает точность до 0,5 угловой секунды. Таким образом, выбранный для проведения эксперимента диапазон углов соответствует телесному углу ОИС, в котором предполагается проводить коррекцию оценок угловых координат по измерениям средних наклонов фазового фронта оптического излучения.
Результаты оценки точности определения азимута и угла места предполагаемого объекта при отсутствии шумов приведены на рисунке 1. Результаты оценки точности определения азимута и угла места предполагаемого объекта по измерениям датчика фазового фронта размером 16´16 для различных степеней турбулентности и при наличии шумов регистрации приведены на рисунке 2.
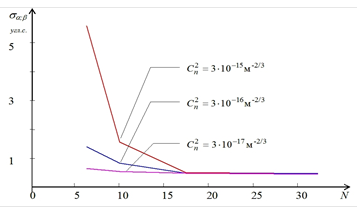
Рис. 1. График зависимости ошибки определения угловых координат объекта от размеров датчика Гартмана при отсутствии шумов в его каналах.
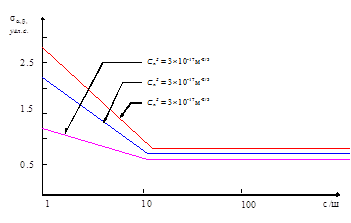
Рис. 2. График зависимости СКО измерений угловых координат от интенсивности шума.
Для выяснения характера зависимости точности измерения угловых координат предполагаемого объекта от величины измеряемых углов проводилась оценка точности измерения различных углов в приведенном выше диапазоне. При этом эксперимент проходил в два этапа. На первом этапе измерялся только азимут предполагаемого объекта при постоянном угле места. На втором - измерялись обе угловые координаты одновременно. Результаты эксперимента показывают, что точность определения обеих координат не зависит от величины измеряемого угла. Таким образом, результаты соответствуют теоретическим положениям о независимости измерений ОИС от средней фазы на апертуре [5]. Кроме этого, из анализа эксперимента видно, что каналы измерения азимута и угла места являются независимыми.
Результаты четвертого эксперимента отражены на рисунке 3.
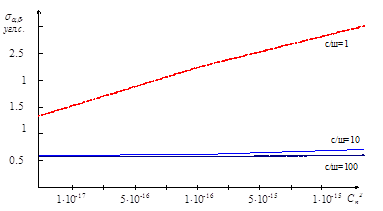
Рис. 3. График зависимости СКО измерений угловых координат от величины турбулентности атмосферы.
Из его анализа видно, что с ростом степени турбулентности атмосферы значительно снижается точность определения угловых координат. Однако применение анализируемого алгоритма определения угловых координат совместно с высокоточными алгоритмами восстановления фазового фронта обеспечивает требуемую точность даже в сильно турбулентной среде. Проведенный вычислительный эксперимент является тому подтверждением.
Выводы
В настоящей работе синтезирован алгоритм совместной компенсации нестационарных искажений оптического излучения, вызванных его распространением в турбулентной атмосфере и измерения угловых координат источника этого излучения. Определение угловых координат осуществляется на базе метода максимального правдоподобия, чем обеспечивается минимизация среднеквадратического отклонения полученных оценок от истинного значения пеленга подвижного объекта. Синтезированный алгоритм предназначен для реализации в АОС фазового сопряжения.
На базе фазового метода пеленгации разработан алгоритм определения ОИС угловых скоростей объекта. Для этого алгоритма проведено обоснование выбора интервалов измерений, обеспечивающих высокую точность оценок угловых скоростей. Он определяется, с одной, стороны быстродействием системы, с другой – временем, в течение которого сохраняется статистическая взаимосвязь турбулентных неоднородностей.
Анализ результатов вычислительного эксперимента показывает:
- размеры датчика фазового фронта существенно влияют на точность получаемых оценок угловых координат. Наиболее сильно такое влияние оказывается в случае слабой турбулентности. Это объясняется тем, что в случае слабой турбулентности к размерам датчика более чувствительна точность восстановления фазового фронта, являющаяся, в свою очередь, составной частью точности измерения угловых координат;
- даже при сильной турбулентности применение датчиков фазового фронта оптической волны больших размеров позволяет с высокой точностью проводить измерения угловых координат объекта. В этом случае применение специальных методов численного дифференцирования, не накапливающих систематическую ошибку, делает возможным получение оценок угловых скоростей объекта с точностью, соответствующей требованиям к перспективным ОИС. При этом точность получаемых оценок прямо пропорциональна расстоянию до цели и обратно пропорциональна ее скорости;
- наличие шумов в каналах датчика фазового фронта оказывает существенное влияние на точностные характеристики синтезированного алгоритма. При этом в случае сильно турбулентной атмосферы влияние шумов регистрации на точность определения угловых координат источника оптической волны проявляется незначительно. Дело в том, что при сильно турбулентной атмосфере оптические аберрации имеют ярко выраженный характер и поэтому эффективно отрабатываются алгоритмами восстановления фазового фронта даже на фоне интенсивных шумов. При слабой турбулентности оптические аберрации на два порядка меньше, вследствие чего их восстановление в условиях интенсивных шумов регистрации несколько усложняется. Однако даже при высоком уровне шумов исследуемый алгоритм обладает высокими точностными характеристиками;
- с ростом степени турбулентности атмосферы значительно снижается точность определения угловых координат. Однако применение синтезированного алгоритма определения угловых координат совместно с высокоточными алгоритмами восстановления фазового фронта обеспечивает требуемую точность даже в сильно турбулентной среде.
Рецензенты:
Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», Минобрнауки России, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Донской государственный технический университет», г. Ростов-на-Дону.
Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, Федеральный научно-производственный центр ФГУП «РНИИРС» г. Ростов-на-Дону.
Библиографическая ссылка
Безуглов Д.А., Юхнов В.И., Енгибарян И.А., Лащенов С.Н. ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ МЕТОДА ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ТОЧЕЧНОГО ИСТОЧНИКА ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ // Современные проблемы науки и образования. 2014. № 3. ;URL: https://science-education.ru/ru/article/view?id=12774 (дата обращения: 11.02.2026).



