Для турбулентного течения газа характерны беспорядочные хаотические пульсации скорости во всех направлениях, придающие всем происходящим процессам стохастический характер - отдельные объемы газа с определенной вероятностью могут перемещаться в любом направлении, и истинное значение любой локальной характеристики газа в конкретный момент времени представляет собой сумму величин, характеризующих основное и пульсационное течения. Следствием хаотических пульсационных движений является беспорядочное интенсивное перемешивание и специфическая турбулентная диффузия, турбулентная вязкость газа, более равномерное, чем при ламинарном течении, распределение осредненной скорости и резкое ее падение в пристенной области, увеличение потерь на трение и т.д.
Мгновенную скорость газа в любой точке потока в каждом из направлений можно представить как сумму осредненной скорости и скорости пульсаций:
wx =`wx + wx¢, wy =`wy + wy¢, wz =`wz + wz¢. (1)
Подстановка этих выражений в уравнения движения Навье-Стокса и усреднение по времени и пространству приводит к уравнениям движения Рейнольдса, в которые входят добавочные касательные напряжения, обуславливающие повышение вязкости и гидравлического сопротивления [5-7]. Для замыкания системы уравнений применяются статистические или полуэмпирические теории турбулентности, используются аналогия между турбулентными и молекулярными напряжениями, экспериментальные данные о статистических связях между пульсациями в пространстве и времени, др. экспериментальные данные [5; 6].
Профиль осредненной осевой скорости газа по сечению канала наиболее точно можно аппроксимировать «универсальным профилем скорости» («трехслойной моделью»), полученным Прандтлем и Тейлором и дополненным Карманом (рис. 1) [10]:
w+ = y+ при y+ < 5 (ламинарный пристенный слой), (2)
w+ = -3,05 + 5ln(y+) при 5 < y+ < 30 (буферный слой), (3)
w+ = 5,5 + 2,5ln(y+) при 30 < y+ < R+ (турбулентное ядро), (4)
где w+ = w/w* - скоростной параметр («универсальная скорость»); y+ = w*ry/m - параметр расстояния трения («универсальная координата»); y - расстояние от стенки, м; w*= (t0/r)1/2 - скорость трения (динамическая скорость), м/с; t0 = lrwcp2/8 - касательное напряжение трения на стенке, Н/м2; l - коэффициент сопротивления; wср - средняя скорость газа, м/с.
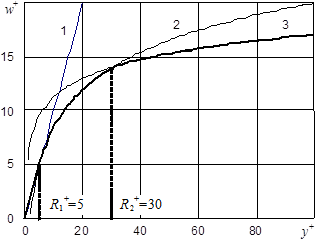
Рис. 1. Универсальный профиль скорости газа при турбулентном режиме течения:
1 - по формуле (2); 2 - по формуле (3); 3 - по формуле (4)
Для оценки коэффициента сопротивления l, необходимого для расчета касательного напряжения на стенке t0 и динамической скорости w*, обычно используются эмпирические зависимости:
- формула Блазиуса (при Re < 105) [1; 2]:
l = 0,3164/Re0,25; (5)
- формула Никурадзе (при Re > 105) [1; 2]:
l = 0,0032 + 0,221/Re0,237; (6)
- формула [2]:
. (7)
Коэффициент сопротивления l и касательное напряжение трения на стенке t0 вычисляются также непосредственно по перепаду давления в канале, которое определяется экспериментально.
При моделировании потоков в цилиндрических трубах можно на основании «универсального профиля» (2)-(4) построить профиль скорости газа без привлечения дополнительных эмпирических и полуэмпирических зависимостей и коэффициентов из условия обеспечения заданных объемного расхода газа или среднерасходной скорости wср.
Расход газа в цилиндрическом канале складывается из расходов в ламинарном пристенном слое, буферном слое и турбулентном ядре, границы между которыми R1 и R2 определяются условиями формул (2)-(4):
W = p(R2-R12)w*w1+ + p(R12-R22)w*w2+ + pR22w*w3+ =
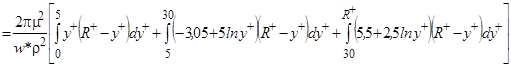. (8)
После интегрирования и преобразований из выражения (8) можно получить соотношение между средней и динамической скоростями газа в виде [6]
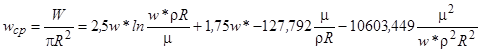(9)
или через динамический критерий Рейнольдса Re* = w*Dr/m = 2w*Rr/m
. (10)
Уравнения (9) и (10) показывают соотношение между средней wср и динамической w* скоростями газового потока в неявном виде. При заданном значении средней скорости уравнение (10) может быть решено итерационными методами. В качестве начального приближения можно использовать известные оценки характеристик турбулентного потока [2]
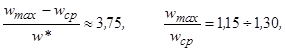(11)
откуда wср/w* » 12,5¸25, причем нижнее значение соответствует малым значениям критерия Рейнольдса (Re » 5000), верхнее - большим (Re » 3×106).
Также в качестве начального приближения можно использовать известное приближенное соотношение [9]
w* » 0,2wср/Re1/8. (12)
Расчеты и сравнение с экспериментальными данными показывают, что формула (10) при Re > 104 позволяет достаточно точно рассчитать и другие параметры потока, в частности - коэффициент сопротивления и, соответственно, гидравлическое сопротивление канала [6].
На рис. 2 показаны профили скорости газа при различных значениях критерия Рейнольдса Re, рассчитанные по формулам (2)-(4) с использованием полученного соотношения (10).
а)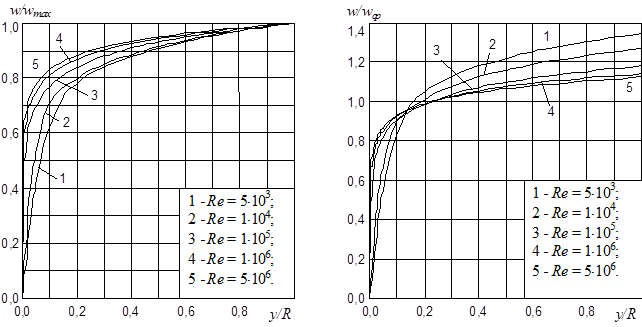 
б)
Рис. 2. Профили скорости газа в турбулентном потоке
Выражения (2)-(4) и (10) дают также возможность рассчитать градиент осевой скорости газа по радиусу канала. После подстановки w+ = w/w* и y+ = w*ry/m можно получить [6]:
dw/dy = r(w*)2/m при 0 < y < 5m/(w*r); (13)
dw/dy = 5w*/y при 5m/(rw*) < y < 30m/(rw*); (14)
dw/dy = 2,5w*/y при 30m/(rw*) < y < R, (15)
или, учитывая, что в цилиндрическом канале y = R - r и dw/dy = -dw/dr,
dw/dr = -2,5w*/(R-r) при 0 < r < R-30m/(rw*); (16)
dw/dr = -5w*/(R-r) при R-30m/(rw*) < r< R-5m/(rw*); (17)
dw/dr = -r(w*)2/m при R-5m/(rw*) < r < R. (18)
Исходные выражения (2)-(4) можно использовать и для двухфазного потока, если определить его транспортные свойства с учетом дисперсной фазы, которые зависят от ее концентрации [6].
В частности, для расчета динамической вязкости двухфазной капельной среды можно использовать соотношение [6]
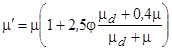, (19)
которое для газодисперсных потоков с твердыми частицами (md >> m) переходит в известную формулу Эйнштейна
m¢ = m(1 + 2,5j). (20)
При небольших концентрациях дисперсной фазы (j << 1) ее влияние на профиль осевой скорости незначительно.
Предложенный подход позволяет с использованием экспериментальных данных и упрощенных представлений о структуре и характеристиках турбулентных потоков газа рассчитать поля скоростей газа. Его использование дает хорошие результаты при расчете как однофазных, так и газодисперсных, газожидкостных (дисперсно-кольцевых) потоков и может использоваться при анализе, интенсификации и оптимизации гидродинамических, тепло- и массообменных процессов в гетерофазных системах в режимах с интенсивным взаимодействием фаз, моделировании и расчетах процессов и аппаратов химических технологий, оценки технологической и социально-экологической эффективности процессов очистки отходящих промышленных газов от пыли [3-8].
Разработанная методика расчета полей скоростей газа использовалась также при анализе движения и расчете равновесных траекторий и концентраций аэрозольных частиц в турбулентном потоке газа [4; 8].
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект 14-06-00256) и Министерства образования и науки Российской Федерации.
Рецензенты:
Войнов Н.А., д.т.н., профессор, Сибирский государственный технологический университет, г. Красноярск.
Чекалов Л.В., д.т.н., генеральный директор ЗАО «Кондор-Эко», Ярославская область, п. Семибратово.
Библиографическая ссылка
Сугак А.В., Сугак Е.В. РАСЧЕТ ПРОФИЛЯ СКОРОСТИ ГАЗА В ТУРБУЛЕНТНОМ ПОТОКЕ // Современные проблемы науки и образования. – 2014. – № 3. ;URL: https://science-education.ru/ru/article/view?id=12756 (дата обращения: 15.09.2024).