Введение. Развитие и усложнение информационно-измерительных систем (ИИС) неизбежно приводит к увеличению количества получаемой, обрабатываемой и передаваемой измерительной информации. Серьёзным препятствием роста объема информации выступает ограниченная пропускная способность каналов связи. В настоящее время ведутся работы по внедрению в состав ИИС более совершенных интерфейсов, однако это требует замены аппаратуры и отраслевых стандартов. Частично проблема может быть решена за счет модернизации аппаратного обеспечения интерфейсов передачи данных, что является длительной и затратной процедурой. Более эффективный путь решения проблемы – разработка методов обработки, сжатия и восстановления информации и соответствующая модернизация программного обеспечения.
Постановка задачи
На сегодняшний день известен ряд методов параметрического анализа (МПА) сигналов, предполагающих наличие некоторой модели сигнала, позволяющих осуществлять сжатие сигналов без потери информации. Среди МПА можно выделить метод наименьших квадратов (МНК) Прони, в основу которого заложена модель, представляющая собой сумму колебательных составляющих разной частоты с соответствующими амплитудами, фазами и затуханиями, наиболее естественно описывающая свободные и вынужденные колебания.
![]()
где p – порядок модели; q – число колебательных и/или инерционных составляющих сигнала; U – амплитуды, a – затухания, f – частоты, j – фазы, a – коэффициенты авторегрессионной модели, ![]() – шаг дискретизации.
– шаг дискретизации.
Применение метода позволяет проводить с высокой точностью измерение параметров колебательных компонент (амплитуд, частот, коэффициентов затухания) на фоне действия шумов и помех [1]. Представляет интерес рассмотреть возможности применения метода для сжатия-восстановления измерительных сигналов ИИС и оценить полученные результаты. Однако реализация метода трудоемка и требует больших вычислительных ресурсов, что препятствует его применению в системах реального времени. Существенно уменьшить трудоёмкость метода возможно, если предварительно выделить знакопеременные составляющие сигнала с последующим оцениванием параметров этих составляющих на основе МНК Прони, задавая порядок модели – не выше второго.
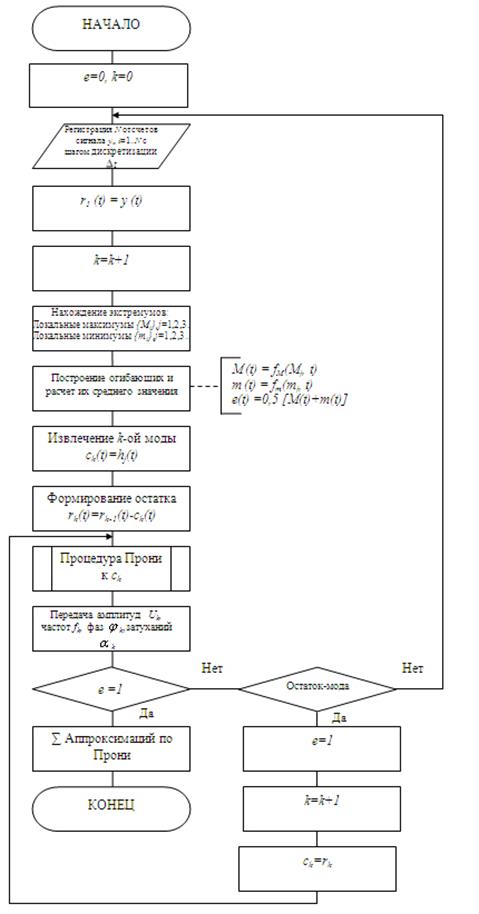
Рисунок 1. Алгоритм реализации метода обработки сигнала на основе комбинации декомпозиции на эмпирические моды и МНК Прони
Метод декомпозиции на эмпирические моды является современным в области цифровой обработки сигналов [10]. Он заключается в разложении исследуемого сигнала на функции, которые должны удовлетворять 2-м необходимым условиям:
1) Общее число экстремумов равняется общему числу нулей с точностью до 1;
2) Полусумма верхней огибающей, интерполирующей локальные максимумы, и нижней огибающей, интерполирующей локальные минимумы, близка к нулю [3,7].
Наиболее часто построение огибающих осуществляется с помощью кубических сплайнов, что обусловлено их высокой гладкостью и фундаментальным свойством, утверждающим, что из всевозможных непрерывных и дважды дифференцируемых функций на любом конечном интервале кубические сплайны минимизируют колебательное поведение функции, следовательно, гарантируют наименьшую интенсивность осцилляций. Выбор сплайнов более высокого порядка обычно нецелесообразен вследствие больших временных затрат на вычисление коэффициентов соответствующих полиномов [8]. Недостатком метода являются временные затраты на вычисления, краевые эффекты (возможными решениями являются включение начального и/или конечного отсчета во множество максимумов и/или минимумов, зеркальное отображение экстремумов, экстраполяция огибающих и т.д.), «недоскоки» и «перескоки» (явления, при которых в промежуточных точках между экстремумами значения сплайна либо намного превосходят, либо намного уступают значениям процесса) [5].
Точность равенства нулю полусуммы 2-х огибающих определяется зашумленностью сигнала, выраженностью краевых эффектов и требуемой точностью. Если 2-е свойство выполняется точно, то речь идет о характеристических модах (гармонический сигнал, ЛЧМ-сигнал, меандр, гауссов радиоимпульс и др.), в противном случае подразумеваются эмпирические моды [6].
Алгоритм обработки сигнала на основе предложенного комбинационного метода представлен на рисунке 1 [2].
Вариант совместного применения метода Прони и EMD-разложения может выглядеть следующим образом:
- Используя метод EMD, получить разложение сигнала на экспериментальные моды.
- Провести процесс отбора значимых мод.
- С помощью метода Прони обработать каждую полученную моду и рассчитать их характеристики [8].
Использование такой комбинации методов (EMD + Прони) позволяет практически решить некоторые проблемы метода Прони, описанные выше:
- уменьшается критичность результата анализа к порядку модели (порядок каждой моды равен 2, или максимум 3);
- уменьшается трудоемкость вычислений параметров составляющих (для каждой моды этот процесс сводится к решению квадратных или кубических уравнений);
- появляется возможность отсеивания шумовой компоненты еще до применения метода Прони [9].
В среде MatLab проведено математическое моделирование комбинационного метода и исследуемо влияние различных факторов на погрешности восстановления сигнала и измерения параметров колебательных компонент сигнала. Установлено, что использование метода позволяет восстанавливать сигнал с погрешностью менее 1 %. Графики некоторых зависимостей приведены на рисунках 2 и 3.
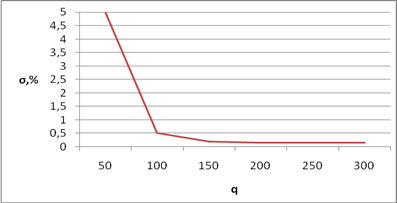
Рисунок 2. График зависимости погрешности восстановления сигнала от отношения сигнал/шум
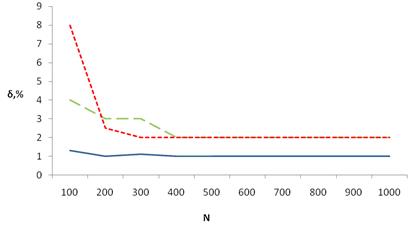
Рисунок 3. Зависимость погрешности измерения частоты от длины выборки N
Коэффициент сжатия, обеспечиваемый применением предложенного алгоритма, возрастает пропорционально увеличению числа отсчетов сигнала k=N/4w, где w – число выделяемых мод сигнала, N – число дискретных отсчетов сигнала.
Оценка времени обработки сигнала зависит от аппаратной реализации, выбранной пользователем, однако наличие информации о тактовой частоте процессора позволяет определять время, затрачиваемое на обработку информации. В нашем случае, при f=2,43 Гц, значения времени обработки сигнала при использовании комбинационного метода EMD+Прони приведены на рисунке 4.
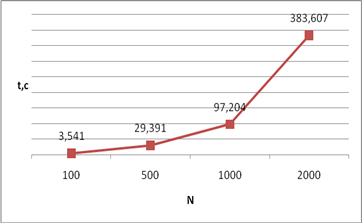
Рисунок 4. Зависимость времени обработки сигнала при использовании комбинаций МНК Прони и декомпозиции на эмпирические моды от числа отсчетов N
Зависимость коэффициента подавления шума в зависимости от отношения сигнал/шум приведена на рисунке 5
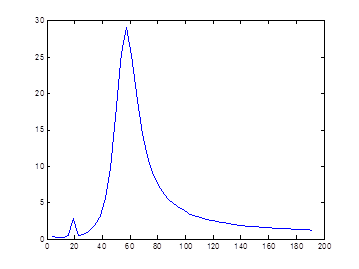
Рисунок 5. Зависимость коэффициента подавления от отношения сигнал/шум
Очевидно, что использование комбинации декомпозиции на эмпирические моды и МНК Прони обеспечивает коэффициент подавления нормального белого шума на уровне 4–5 раз.
На основании разработанных методов автором предложено построение адаптивной ИИС, предназначенной для сжатия и восстановления сигналов с одновременным измерением параметров их колебательных компонент на основе комбинации МНК Прони и метода декомпозиции на эмпирические моды.
Данная система предназначена для удаленного доступа к информации о состоянии технически сложных объектов. Система позволяет следить в реальном времени за состоянием объекта наблюдения, анализировать причины неполадок, а также настраивать систему на выполнение специальных действий при наличии событий определенного типа. Блок управления опросом системы (рис. 6) осуществляет опрос датчиков физических величин, при этом частота и порядок опроса датчиков задается программно. После завершения цикла опроса устройство переходит к первичной обработке результатов измерения. Блок задания кадра служит для определения длины кадра в зависимости от числа выделяемых знакопеременных составляющих сигнала. После разложения производится обработка полученных результатов по методу Прони, определяются физические параметры колебательных компонент сигнала. Далее параметры, определенные в блоке преобразования Прони, передаются на блок формирования пакетов, где в соответствии с принятым протоколом формируются выходные данные. После прохождения блоков декодирования и восстановления данных сигнал поступает на интерфейс оператора. Организация данных, получены в процессе обработки сигнала, подробно рассмотрена в [4].
Свойство адаптивности реализовано в данной системе за счет выбора оптимального числа параметров сжатия в зависимости от характеристик входного сигнала.
Ключевым элементом данной адаптивной системы является обратная связь, реализованная за счет добавления блока задания кадра и алгоритма обработки (количество выделяемых знакопеременных составляющих).
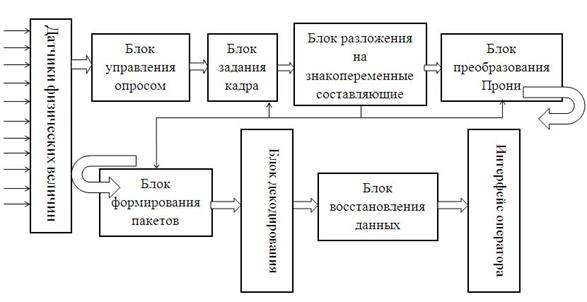
Рисунок 6. Структурная схема ИИС
Заключение. В результате проведенной работы были выявлены факторы, обуславливающие погрешность определения параметров гармонического сигнала и погрешность восстановления комбинационным методом, включающим в себя декомпозицию на эмпирические моды и процедуру Прони. К этим факторам относятся параметры регистрации (длина реализации, число периодов), оцифровки (разрядность АЦП, шаг дискретизации), условия воспроизведения сигнала (амплитуда и фаза сигнала, уровень шума, частота гармонической помехи).
Оценены коэффициент подавления шума, свидетельствующий о хорошей помехоустойчивости метода даже при низких значениях отношения сигнал/шум и время обработки сигнала на основе предложенного метода. Приведена структура ИИС, включающая в себя блоки обработки данных на основе предложенного алгоритма.
Рецензенты:
Трофимов А.А., д.т.н., доцент, заместитель начальника учебно-научного центра ОАО «НИИФИ», г. Пенза.
Бодин О.Н., д.т.н., профессор кафедры «ИИТ» ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.
Библиографическая ссылка
Терехина А.В. СОВЕРШЕНСТВОВАНИЕ ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНЫХ СИСТЕМ ПУТЕМ МОДЕРНИЗАЦИИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12675 (дата обращения: 13.02.2026).



