Введение
Экспериментальные исследования древесины при кратковременном и длительном загружениях выявили существенную нелинейность ее поведения при различных схемах загружения. Нелинейность проявляется даже при относительно небольших напряжениях. В связи с этим одно из важнейших направлений в совершенствовании норм проектирования деревянных конструкций – учет длительной прочности и ползучести древесины.
Экспериментальные исследования ползучести древесины
Экспериментальные исследования при длительном загружении выявили, что деформации ползучести зависят от ряда факторов [8]: вид и уровень нагрузки, влажность, температура и др. На рис. 1 показана зависимость характеристики ползучести 
от вида нагрузки.
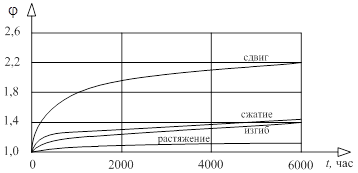
Рис. 1. Характеристики ползучести в зависимости от вида нагрузки
Зависимости деформаций ползучести от уровня нагрузки при сжатии и изгибе представлены на рис. 2 и 3.
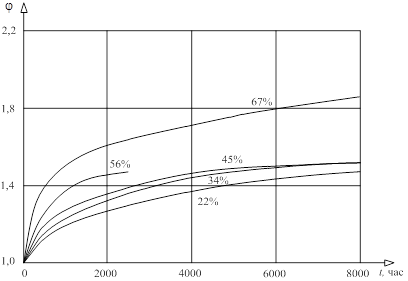
Рис. 2. Характеристики ползучести при сжатии в зависимости от уровня нагрузки в % от кратковременного предела прочности
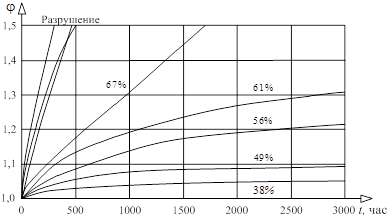
Рис. 3. Характеристики ползучести при изгибе в зависимости от уровня нагрузки в % от кратковременного предела прочности
Результаты исследований ползучести древесины показывают существенную зависимость характеристик ползучести при различных видах приложения нагрузки и различных уровнях нагружения. Таким образом, экспериментальные данные по кривым характеристик ползучести древесины указывают на необходимость учета нелинейной ползучести, а также влияния диаграммы мгновенного деформирования в уравнениях ползучести.
Уравнения ползучести древесины
Обстоятельный обзор по уравнениям механического состояния древесины содержится в диссертации К.П. Пятикрестовского [5]. Из обзора видно, что для описания ползучести древесины предложено два интегральных уравнения линейной ползучести.
Во-первых, это уравнение наследственной теории пластичности, предложенное А.Р. Ржаницыным к описанию ползучести древесины [6]:
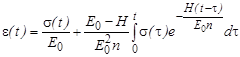, (1)
где E0 – мгновенный модуль упругости (E0=1,48·104 МПа); H – длительный модуль упругости, который принимает значения H=(0,6÷0,75)E0; n – время релаксации, в зависимости от вида напряженного состояния n=10-25 суток (обычно принимают среднее значение).
К этой группе моделей применяют уравнение Максвелла, использованное Е.Н. Квасниковым [3]:
, (2)
где k – коэффициент вязкости (
), или коэффициент внутреннего сопротивления деформации.
На основании многочисленных экспериментов Е.А. Квасников определил соотношение 
в следующем виде:
, (3)
где n*=0,38 – коэффициент, характеризующий нелинейность вязкого сопротивления.
Уравнение ползучести древесины записано в линейном виде:
. (4)
Во-вторых, это линейная теория наследственной ползучести Максвелла-Арутюняна, использованная И.Е. Прокоповичем и В.А. Зедгенидзе для описания ползучести древесины [4]:
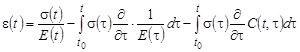, (5)
где 
; С0=2,87·10-5 (МПа)-1, А=10,95 (МПа)-1; B1=1; γ=γ1=0,15 (1/сут).
А.Р. Ржаницын осуществил усовершенствование уравнения линейной ползучести с помощью способа А.Ю. Ишлинского:
, (6)
где H – длительный модуль упругости; E0 – мгновенный модуль упругости; n – время релаксации.
Академик А.Ю. Ишлинский [2] добавил в уравнение
(7)
постоянное слагаемое, зависящее от предела текучести материала σS:
, (8)
где b, n1, r – физические константы тела по А.И. Лурье: b – модуль упругости; n1 – коэффициент интенсивности упругого последействия, r – коэффициент интенсивности релаксации напряжений.
А.Р. Ржаницын на основании способа А.Ю. Ишлинского предложил для древесины два варианта уравнения нелинейной ползучести [7]. В первом варианте он отбросил в левой части уравнения (6) второе слагаемое, превратив его в уравнение Максвелла:
. (9)
Затем он добавил в правой части слагаемое в виде предела текучести древесины sТ:
. (10)
Переход к этому уравнению от уравнения (6) осуществляется в момент t1 достижения полной деформацией древесины значения 
.
Использование уравнения (10) прекращается в момент времени t2 достижения полной деформацией древесины значения 
, где F представляет собой отрицательный длительный модуль упругости (константа) в неустойчивой стадии деформирования.
Для этой же стадии линейное уравнение ползучести записывается в следующем виде:
. (11)
Линейные дифференциальные уравнения (10) и (11) решаются обычными методами линейной теории ползучести.
Аппроксимация экспериментальных данных характеристик ползучести
В теории ползучести и Еврокодах используется характеристика ползучести φ(t), представляющая собой отношение деформации ползучести 
к первоначальной мгновенной деформации 
:
. (12)
Функция 
получается на основе обработки экспериментов и записывается в виде:
, (13)
где 
- предельное значение характеристики ползучести.
Обработка экспериментальных кривых ползучести позволила получить кривые зависимости предельных значений характеристик ползучести φ∞ в зависимости от уровня напряжения 
(рис. 4).
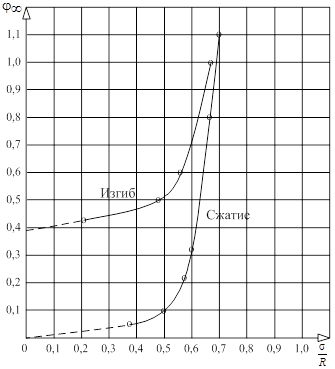
Рис. 4. Экспериментальные данные и аппроксимация значений φ∞
Из данных рис. 4. видно, что характеристика ползучести древесины при сжатии и при изгибе в области малых и средних значений существенно различна.
Значения предельной характеристики ползучести древесины 
аппроксимируем полиномом третьей степени. Для случая работы древесины на сжатие получаем:
. (14)
Для случая работы древесины на изгиб:
. (15)
В работе [1] для нахождения длительной критической силы 
предлагается квадратное уравнение:
, (16)
где 
- значение критической силы Эйлера, F – площадь поперечного сечения.
Таким образом, уравнение (18) позволяет найти длительную несущую способность для сжатого деревянного элемента через критическую силу Эйлера с учетом ползучести древесины.
Выводы
1. Экспериментальные данные по кривым характеристик ползучести древесины указывают на необходимость учета нелинейной ползучести, а также влияния диаграммы мгновенного деформирования в уравнениях ползучести.
2. В существующих моделях длительной прочности не учитывается одновременно мгновенная нелинейность и нелинейная ползучесть древесины.
3. Обработка экспериментальных данных позволила получить аналитические выражения характеристик ползучести в зависимости от уровня напряжений. Аппроксимирующие зависимости могут быть использованы для нахождения длительной несущей способности для сжатого деревянного элемента через критическую силу Эйлера с учетом ползучести древесины.
Рецензенты:
Санжаровский Р.С., д.т.н., профессор кафедры «Строительные конструкции», ФГБОУ ВПО «Новгородский государственный университет имени Ярослава Мудрого», г. Великий Новгород.
Швецов И.В., д.т.н., заведующий кафедрой «Промышленная теплоэнергетика», ФГБОУ ВПО «Новгородский государственный университет имени Ярослава Мудрого», г. Великий Новгород.
Библиографическая ссылка
Вареник А.С., Вареник К.А. О ПОЛЗУЧЕСТИ ДРЕВЕСИНЫ // Современные проблемы науки и образования. – 2014. – № 2. ;URL: https://science-education.ru/ru/article/view?id=12663 (дата обращения: 08.10.2024).