Microsoft PowerPoint – широко распространенная в настоящее время программа для разработки и проведения презентаций с использованием компьютера. Она обладает большими возможностями по представлению текстовых документов, таблиц, графической информации и т.п. Кроме того, PowerPoint можно использовать для создания анимированных клипов, демонстрацией которых сопровождается объяснение нового материала, в том числе и в курсе математики [1, 2, 5].
При использовании метода презентации интенсификация обучения достигается за счет более высокой, чем при традиционных методах обучения, степени наглядности, поскольку появляется возможность превратить наглядность из статической в динамическую. Таким образом, в процесс восприятия учебной информации вовлечены большинство чувственных компонентов обучаемого, что оказывает непосредственное влияние на скорость и эффективность восприятия материала. Кроме того, появляется возможность широкого тиражирования обучающего материала, его использования при организации самостоятельной работы и дистанционном обучении.
При проведении практических занятий по математике в вузе следует уделять особое внимание включению механизмов активизации умственной деятельности студентов через проведение обучения обобщениями и схемами. Не следует предлагать готовые решения, важно сделать своих слушателей участниками процесса поиска решения, формулируя дополнительные вопросы и обсуждая вслух каждый этап решения задачи. При таком способе подачи информации преподаватель имеет возможность не только представить необходимый материал, но и передать свое отношение к нему, формальное восприятие заменить творческим процессом и вовлечь в этот процесс студентов.
Основной принцип при совместном решении задачи и построении схемы решения состоит в том, что сложная мысль разделяется на элементарные звенья, выделяются основные этапы развития представлений. Следует акцентировать внимание на процессы мышления, кажущиеся на первый взгляд элементарными, само собой разумеющимися, но которые на самом деле требуют большой работы мысли обучаемых.
После записи условия задачи преподавателя интересует ряд вопросов:
- Как студент воспринимает условие?
- Что он делает дальше?
- О чем и как он думает?
- Каковы дальнейшие этапы его мысли на пути решения задачи?
При ответе на эти вопросы и возникают соответствующие элементы схемы.
В качестве примера приведем схему, используемую при вычислении неопределенного интеграла ![]() . Схема анимирована в программе Microsoft Power Point (рис. 1).
. Схема анимирована в программе Microsoft Power Point (рис. 1).
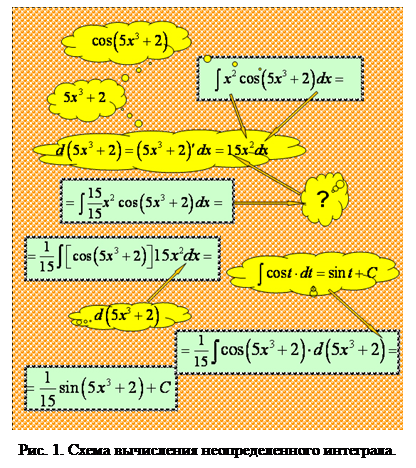
Комментарии к кадрам:
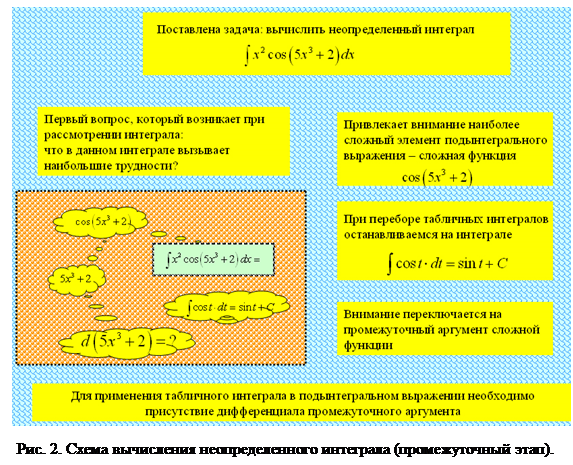
Кадр 1. Поставлена задача вычислить неопределенный интеграл ![]() .
.
Первый вопрос, который возникает при рассмотрении интеграла: что в нем вызывает наибольшие трудности?
Кадр 2. Привлекает внимание наиболее сложный элемент подынтегрального выражения – сложная функция ![]() .
.
Кадр 3. При переборе табличных интегралов останавливаемся на интеграле ![]() .
.
Кадр 4. Внимание переключается на промежуточный аргумент сложной функции ![]() .
.
Кадр 5. Для применения табличного интеграла в подынтегральном выражении необходимо присутствие дифференциала промежуточного аргумента ![]()
Кадр 6. Следующий этап решения – формирование дифференциала промежуточного аргумента из фрагментов подынтегрального выражения ![]() .
.
Кадр 7-9. В подынтегральном выражении присутствуют необходимые для этой цели множители ![]() и
и ![]() , однако отсутствует коэффициент 15.
, однако отсутствует коэффициент 15.
Кадр 10. Для достижения поставленной цели в подынтегральное выражение вводится необходимый множитель 15, а вызванные им изменения устраняет компенсирующий это действие делитель 15
![]() .
.
Кадр 11-12. В дальнейшем делитель выносится за знак интеграла, а введенный множитель 15 вместе с множителем ![]() формирует дифференциал промежуточного аргумента
формирует дифференциал промежуточного аргумента
![]() .
.
Кадр 13-15. В итоге получаем интеграл, который вычисляем по формуле из таблицы интегралов
![]() .
.
В конечном итоге, готовая схема выглядит, как показано на рис. 1.
Последовательное появление отдельных элементов схемы, высвечивание связей между ними позволяет проследить во всех подробностях поиск плана решения и его поэтапную реализацию от обнаружения сложной функции и формирования дифференциала ее промежуточного аргумента до выхода на табличный интеграл. Применение различных визуальных эффектов позволяет на всех этапах акцентировать внимание студентов на возникающих проблемах и способах их решения. Предложенная схема может быть использована в дальнейшей работе как алгоритм для вычисления интегралов методом непосредственного интегрирования [3].
Изложение теоретического материала в курсе математики требует доказательства множества утверждений, что усложняет восприятие слушателями излагаемого материала. Необходимо использовать такие средства обучения, которые на начальной стадии изучения темы позволят акцентировать внимание на ключевых моментах, отслеживать развитие идей и формирование связей между фрагментами излагаемого материала. Для достижения этой цели применяются различные схемы с подробными описаниями взаимосвязей между их элементами [4]. Такой подход приводит к созданию достаточно четко оформленного силуэта изучаемого раздела до того, как при детальном рассмотрении отдельных вопросов громоздкие математические преобразования начнут заслонять основную нить изложения. Дальнейшее детальное изучение отдельных вопросов идет в форме наполнения предложенной схемы, которая по мере заполнения приобретает все более отчетливые очертания, в конечном итоге формируя законченный образ изучаемого раздела.
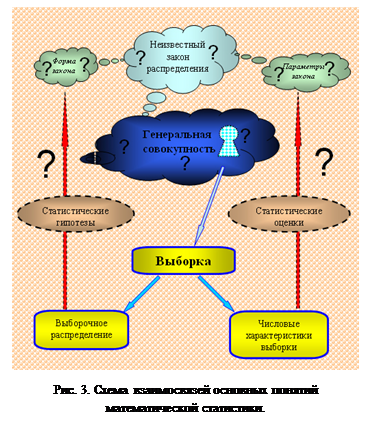
Например, на схеме, анимированной в программе Microsoft PowerPoint (рис. 3), обсуждаются основная задача математической статистики, а также вытекающие из нее вспомогательные задачи и подходы к поиску их решения. Введение в круг задач математической статистики предназначено для того, чтобы сформировать у студентов эскизную структурную схему предмета уже на начальном этапе его изучения.
Комментарии к кадрам:
Кадр 1. Математическая статистика так же, как и теория вероятностей, занимается изучением закономерностей массовых случайных явлений. Подход к исследованиям: в теории вероятностей – теоретический, в математической статистике – эмпирический. Один из основных объектов исследования математической статистики – случайные величины. Основная задача математической статистики – восстановление неизвестного закона распределения случайной величины.
Кадры 2-6. Множество значений случайной величины составляет генеральную совокупность. Стоит задача нахождения неизвестного закона распределения случайной величины в генеральной совокупности. Эта задача распадается на две части: установление формы закона распределения и оценка параметров этого закона. Особенность ситуации заключается в том, что этот объект (генеральная совокупность) недоступен для непосредственного изучения, и потому решение поставленных задач требует специального подхода.
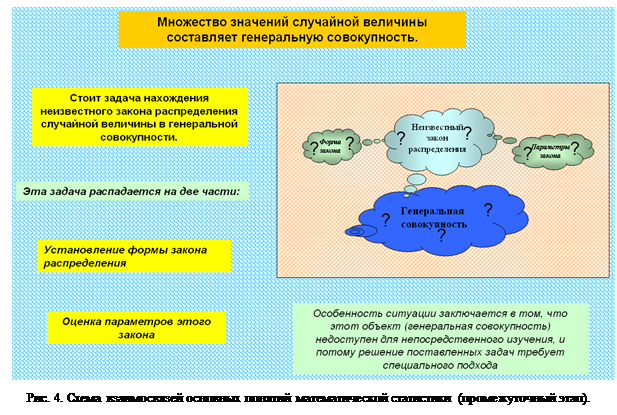
Кадры 7-10. Выходом из создавшейся ситуации служит возможность получить информацию из доступной части генеральной совокупности. Эта часть генеральной совокупности (выборка) доступна для непосредственного изучения. В результате такого изучения могут быть найдены: выборочное распределение случайной величины и выборочные числовые характеристики случайной величины.
Кадр 11-15. Эти результаты дают приближенное представление о теоретическом законе распределения случайной величины в генеральной совокупности. Выборочное распределение случайной величины несет в себе информацию о форме ее закона распределения в генеральной совокупности. Выборочные числовые характеристики случайной величины приблизительно характеризуют значения параметров теоретического закона распределения. На выбранном пути остается ряд нерешенных вопросов. В какой степени можно доверять высказанному по результатам выборочных наблюдений предположению о форме теоретического закона распределения? С какой точностью выборочные характеристики оценивают неизвестные параметры теоретического закона распределения?
Кадр 16-19. Для решения первого из этих вопросов применяются статистические гипотезы. Разработанный математический аппарат позволяет по результатам наблюдений предсказать степень достоверности высказанных предположений. Для решения второго вопроса применяются статистические оценки. Использование интервальных оценок позволяет по данным выборки построить интервалы значений, в которых с заданной доверительной вероятностью заключены неизвестные параметры теоретического распределения.
Кадр 20. На приведенной схеме отражены маршруты переходов от полученных в выборке результатов наблюдений к неизвестному закону распределения случайной величины и к оценкам всех неизвестных параметров этого закона. Сплошные стрелки свидетельствуют о возможности вычисления указанных величин на базе выборочных данных, пунктирные стрелки подчеркивают вероятностный характер связей.
Все понятия, присутствующие на итоговой схеме, а также показанные стрелками связи между ними, в дальнейшем подробно рассматриваются в отдельных параграфах раздела. Подчеркнем, что на начальном этапе внимание акцентируется исключительно на предназначении используемых характеристик и основных чертах их взаимоотношений, а при подробной проработке материала рекомендуется периодически возвращаться к данной схеме, отслеживая процесс накопления информации и определяя ее место в схеме. Таким образом, в целом предложенная схема представляет собой замкнутую систему вспомогательных задач с четко обозначенными логическими связями между ними. Это позволяет при дальнейшем более подробном изложении материала наглядно иллюстрировать процесс наполнения информацией такой схемы и комментировать этапы этого процесса, акцентируя внимание на причинах, которые вызывают необходимость поиска новых числовых характеристик и формулировку новых задач.
Такой подход в конечном итоге способствует формированию у студентов законченного образа математической статистики и позволяет при дальнейшем подробном рассмотрении отдельных вопросов более осознанно подходить к решаемым задачам, на новом уровне высвечивая логические связи раздела.
Рецензенты:
Бубнов В.А, д.т.н., профессор, заведующий кафедрой естественнонаучных дисциплин Института математики и информатики ГБОУ ВПО «Московский городской педагогический университет», г. Москва.
Полтавский А.В., д.т.н., профессор, профессор кафедры естественнонаучных дисциплин Института математики и информатики ГБОУ ВПО «Московский городской педагогический университет», г. Москва.
Библиографическая ссылка
Анисова Т.Л., Марков В.К., Устинова Л.В. ИСПОЛЬЗОВАНИЕ МЕТОДА ПРЕЗЕНТАЦИИ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ В ВУЗЕ // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12576 (дата обращения: 13.02.2026).



