Простейшим приближением, в котором можно выполнить расчет течения газа в сопловых каналах турбин, является приближение, подобное одномерному (квазиодномерное). В этом приближении учитывается изменение площади поперечных сечений канала, хотя в каждом таком сечении газодинамические параметры считаются постоянными [4]. У этой математической модели есть по крайней мере два применения. Первое связано с быстрым предварительным расчетом, т.к. расчет уже в двумерном приближении требует использования численных методов. Второе применение квазиодномерного расчета связано как раз с многомерными численными расчетами. В настоящее время в большинстве численных методов для получения стационарного решения используется процедура установления [2; 3]. Для таких алгоритмов необходимо задавать начальные условия. Оптимальным для этих целей следует считать квазиодномерный расчет.
С наибольшей точностью квазиодномерное приближение применяется к плоско- и осесимметричным каналам с плавно изменяющейся образующей. Для применения этого приближения к турбинным решёткам в работе [1] предлагается процедура спрямления канала.
В данной работе рассчитывается течение воздуха в осевых турбинах, экспериментально исследованных в [7; 8]. Особенностью сопловых каналов этих турбин является наличие косого среза. Один из таких каналов (С-5, по терминологии работы [7]) приведен на рис. 1а. Относительные пропорции геометрии канала на этом рисунке соблюдены. Точка D расположена там, где касательная из точки B отходит от образующей спинки лопатки BC, f *– линейный размер критического сечения AB, f – линейный размер косого среза AC.
Квазиодномерные расчеты
Применим процедуру спрямления [1] для канала 1а. Получим несимметричный канал, приведенный на рис. 1б. Для применения квазиодномерного приближения рассмотрим два симметричных канала: сопло Лаваля (рис. 1в) и конфузорное сопло (рис. 1г).
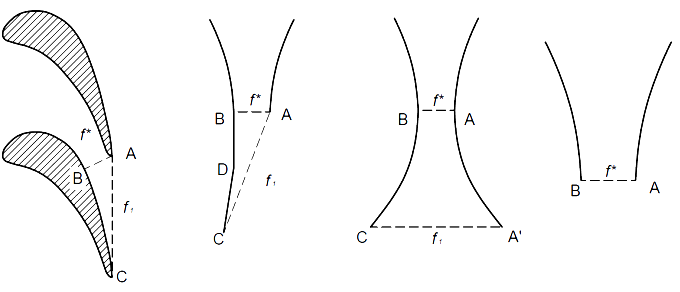
а) б) в) г)
Рис. 1. Межлопаточный канал: а – исходный; б – спрямленный, несимметричный; в – спрямленный, симметричный, сопло Лаваля; г – спрямленный, симметричный, конфузор.
Выполним расчеты течения воздуха в этих каналах (рис. 1 в, г) с целью решения вопроса о наибольшей эквивалентности течению в исходном канале (рис. 1а). Исходными данными для расчетов являются следующие значения [7]; f/f*=2.36; pa/p0=0,203; где p0 – давление торможения на входе; pa – противодавление.
Рассмотрим сильно упрощенную модель – сопло Лаваля (рис. 1в). По отношению f/f*, которое равно отношению площадей поперечных сечений, найдем характерные числа Маха (M) из уравнения
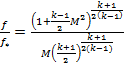 , (1)
, (1)
где k – показатель адиабаты.
Трансцендентное уравнение (1) решалось численным методом. Получены два характерных числа Маха для до- и сверхзвукового истечения: М’=0,255 и М’’=2,38. Соответствующие давления p’и p’’ найдены из газодинамической функции
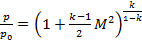 (2)
(2)
Характерные отношения давления будут иметь значения p’/p0=0,956; p’’/p0=0,071.
Отметим, что давление торможения здесь также относится к области входа в канал. Отношение критического давления к давлению торможения для воздуха имеет значение p*/p0=0,528.
Характерные значения отношения давлений приведены на рис. 2. Ось X направлена по тракту сопла, верхняя кривая соответствует дозвуковому истечению, а нижняя – сверхзвуковому, расчетному.
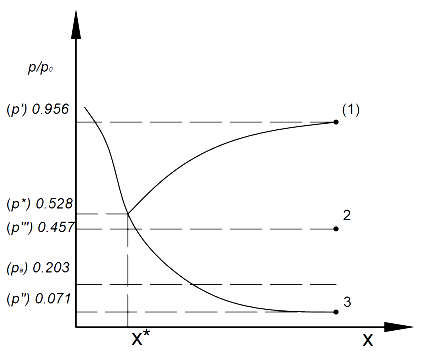
Рис. 2. Характерные давления для сопла Лаваля.
Ещё одно характерное значение давления находится из соотношения для прямого скачка уплотнения на срезе
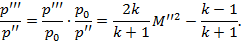 (3)
(3)
В формуле (3) также предполагаем, что давление торможения до среза сопла не изменяется. Из этой формулы получаем следующее значение: p’’’/p0=0,457.
Таким образом, при противодавлениях выше точки (1) будет происходить дозвуковое истечение (режим трубки Вентури); при противодавлениях между точками (1) и (2) – также дозвуковое истечение, но с прямым скачком уплотнения внутри сверхзвуковой части сопла; при противодавлении, расположенном ниже точки (2), будет осуществляться сверхзвуковой расчетный режим. При этом если противодавление расположено между точками (2) и (3) – режим перерасширения, с образованием скачков уплотнения за срезом, в которых выходное давление p’’ повышается до противодавления pa.. При противодавлении ниже точки (3) осуществляется режим недорасширения. В этом случае выходное давление за срезом будет понижаться до противодавления за счет волн разряжения.
Заданное противодавление pa/p0=0,203 соответствует сверхзвуковому режиму перерасширения. Таким образом, истечение будет происходить с числом Маха M’’=2,38; за срезом сопла давление будет повышаться от p’’/p0=0,071 до противодавления pa/p0=0,203 за счет косых или мостообразных скачков уплотнения в струе. Скорость течения при этом будет понижаться, а струя сужаться.
Особенностью спрямленного сопла (рис. 1б) является то, что угловая точка А в критическом сечении одновременно расположена на косом срезе АС. Таким образом, можно рассмотреть течение газа в конфузорном сопле (рис. 1г).
Если pa/p0 < p*/p0, что соответствует нашему случаю (0,203<0,528), то течение в критическом сечении будет звуковым. Часто констатацией этого факта и ограничиваются при рассмотрении течений в конфузорном сопле [1]. Однако пониженное противодавление будет приводить к расширению потока и ускорению его. При этом необходимо учитывать, что из-за периодичности решетки существует поджатие «свободной» струи от соседних сопел. Если бы течение за срезом происходило без потерь, то максимальное значение числа Маха могло быть найдено по газодинамической функции (2). Отсюда выражение для числа Маха примет вид:
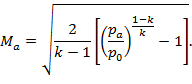 (4)
(4)
Для заданного pa/p0=0,203 максимальное число Маха будет иметь следующее значение Мa=1,7.
Таким образом, можно предположить, что конфузорное сопло (рис. 1г), с учетом поджатия струи от соседних каналов, будет сверхзвуковым на некотором удалении от среза. Особенностью истечения из этого сопла является то, что максимальное значение числа Маха зависит от противодавления, в отличие от сопла Лаваля (рис. 1в).
Для проверки этой гипотезы были выполнены расчеты течения воздуха в межлопаточном канале (рис. 1а) в двумерном приближении.
Сравнение с двумерными расчетами
Течение воздуха в межлопаточном канале реактивной турбинной решетки (рис. 1а) было также рассчитано в двухмерном приближении разработанным комплексом программ. Алгоритм расчета и особенности его применения описаны в работах [3; 5; 6].
Отметим здесь, что исходной математической моделью являлись интегральные уравнения газовой динамики. Это позволило использовать неортогональную разностную сетку. Такая сетка дает возможность избежать измельчения разностных ячеек вблизи твердых границ и не вносить нерегулярного проявления схемной вязкости в расчетах [3].
Результаты двумерных расчетов приведены на рис. 3 и 4. На этих рисунках изображены рассчитанные изолинии чисел Маха для разных противодавлений. Пунктирные линии, исходящие из угловой точки А, соответствуют волнам разряжения. Веер слабых волн разряжения должен также исходить и из точки D. Для их точной локализации по расчетным данным необходимо использовать значительно более мелкую разностную сетку.
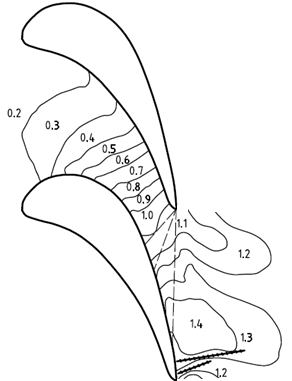
Рис. 3. Двухмерный расчет течения газа в сопле с косым срезом; pa/p0=0,203.
На рис. 3 и 4 «цепными» линиями отмечены косые скачки уплотнения, расположенные внизу спинки лопатки. Перед ними, вблизи точки D, находится область максимальных чисел Маха. При этом значения этих чисел зависят от противодавления за косым срезом.
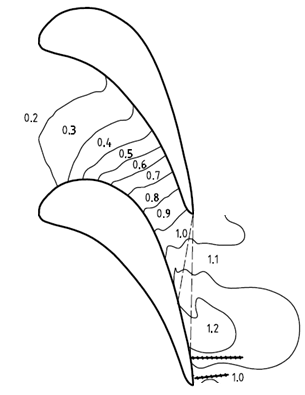
Рис. 4. Двухмерный расчет течения газа в сопле с косым срезом; pa/p0=0,297.
Заключение
Выполненные двумерные расчеты показали, что максимальное значение числа Маха зависит от противодавления за срезом сопла.
В случае спрямления межлопаточного канала, для квазиодномерного приближения, такая же зависимость есть для течения в конфузорных каналах, с учетом поджатия струи от соседних сопел.
В квазиодномерных расчетах числа Маха получились завышенными по сравнению с двумерными расчетами (табл. 1).
Таблица 1
|
pa/p0 |
Максимальное число Маха |
|
|
квазиодномерный расчет |
двумерный расчет |
|
|
0,203 |
1,7 |
1,4 |
|
0,297 |
1,5 |
1,2 |
Это можно объяснить образованием косых скачков уплотнения, полученных в двумерных расчетах (рис. 3 и 4). Отсюда получаются дополнительные потери, приводящие к потере скорости потока.
Таким образом, для расчетов в квазиодномерном приближении можно рекомендовать канал, приведенный на рис. 1г. При этом, с учетом поджатия струи соседними каналами, максимальное число Маха можно рассчитывать по газодинамической функции (4). Естественно, необходимо в этом приближении рассчитывать поворот потока в косом срезе по известной методике.
Рецензенты:
Зуев В.А, д.т.н., профессор, заведующий кафедрой «Кораблестроение и авиационная техника» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород.
Грамузов Е.М, д.т.н., профессор, заведующий кафедрой «Аэро-гидродинамика, прочность машин и сопротивление материалов» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород.
Библиографическая ссылка
Косолапов Е.А., Рамс Э.Э., Соленников М.Д., Хрунков С.Н. КВАЗИОДНОМЕРНЫЙ РАСЧЕТ ТЕЧЕНИЯ ГАЗА В ТУРБИННЫХ СОПЛАХ С КОСЫМ СРЕЗОМ // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12571 (дата обращения: 13.02.2026).



