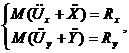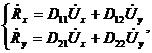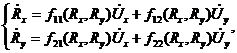Введение
Для учета пластического ресурса рамных конструкций при сейсмических воздействиях широко используется упругопластическая модель с одной степенью свободы, которая не позволяет с достаточной надежностью выявить пластический резерв рамных конструкций. Для выполнения надежных, адекватных реальности расчетов приходится создавать модели рамных конструкций большой размерности и использовать для их анализа сложные программные комплексы (ПК). В [4] профессор Рутман Ю.Л. предлагает обобщение упругопластической модели с одной степенью свободы на случай произвольной системы с n степенями свободы. Такую обобщенную модель он называет макромоделью. Обобщенная модель позволяет учитывать взаимодействие компонентов реакции упругопластической системы. Это взаимодействие оказывает большое влияние на характер процесса при сложном (непропорциональном по компонентам) нагружении. Для работы с этой моделью достаточно использования ПК типа MathCAD или MATLAB. Адекватность макромодели была проверена в [1]. Необходимым условием применения этого метода является отыскание поверхностей текучести рамных конструкций (геометрическое место точек, соответствующих компонентам обобщенной предельной реакции рамной конструкции, при возникновении которой она превращается в механизм). Допускается считать работу конструкции внутри поверхности текучести чисто упругой, и, как только обобщенная реакция рамной конструкции достигает любой точки поверхности текучести, рамная конструкция превращается в механизм. В [1] были предложены методы построения и исследования поверхностей текучести. Поверхность текучести систем с двумя степенями свободы представляет собой плоскую фигуру. Чем больше степеней свободы имеет система, тем большей размерностью обладает поверхность текучести.
Из [4] уравнения упругопластической макромодели для системы с двумя степенями свободы имеют вид (1–3).
Уравнение движения приведенной массы M:
в условиях упругой работы конструкции имеем
в условиях упругопластической работы имеем
где ![]() –
проекции ускорения основания рамы на оси X,
Y;
–
проекции ускорения основания рамы на оси X,
Y; ![]() –
проекции на оси X, Y ускорения массы М относительно основания;
–
проекции на оси X, Y ускорения массы М относительно основания; ![]() – проекции на оси X, Y
усилий взаимодействия между массой и рамой;
– проекции на оси X, Y
усилий взаимодействия между массой и рамой; ![]() –
упругие жесткости системы;
–
упругие жесткости системы; ![]() – коэффициенты
зависимости между скоростями обобщенных перемещений и усилий, которые
определяются из уравнения поверхности текучести рамной конструкции. Аналитическая
аппроксимация этой поверхности текучести или ее части имеет вид
– коэффициенты
зависимости между скоростями обобщенных перемещений и усилий, которые
определяются из уравнения поверхности текучести рамной конструкции. Аналитическая
аппроксимация этой поверхности текучести или ее части имеет вид ![]() .
.
Результаты исследования ряда широко используемых рамных конструкций в [3] показали, что поверхности текучести рамных конструкций имеют вид многоугольников. Чем больше статическая неопределимость рамы и чем больше число вариантов ее возможных механизмов, тем больше сторон у многоугольника, т.е. поверхность текучести приближается к эллипсу. Расчетный анализ показал, что замена многоугольника текучести эллипсом дает погрешность порядка 10-20%, что допустимо для инженерных расчетов.
Реализация метода макромодели в ПК MathCAD без учета упрочнения материала конструкций
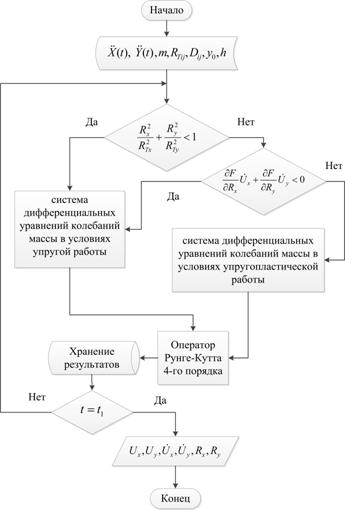
Алгоритм программы динамического расчета по методу макромодели без учета упрочнения материала конструкций представлен на рисунке 1.
Рис. 1. Алгоритм динамической макромодели без учета упрочнения материала конструкций
где ![]() –
инструментальные или синтезированные акселерограммы; m – значение сосредоточенной приведенной массы;
–
инструментальные или синтезированные акселерограммы; m – значение сосредоточенной приведенной массы; ![]() – упругие жесткости системы, получаемые
из упругого расчета по двум направлениям;
– упругие жесткости системы, получаемые
из упругого расчета по двум направлениям; 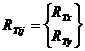 –
вектор предельных нагрузок, радиусы эллипса (поверхности текучести);
–
вектор предельных нагрузок, радиусы эллипса (поверхности текучести); ![]() – вектор начальных условий;
– вектор начальных условий; ![]() – шаг интегрирования;
– шаг интегрирования; 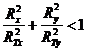 – условие текучести системы;
– условие текучести системы; ![]() – условие разгрузки.
– условие разгрузки.
В качестве тестового примера однопролетная рама с сосредоточенной массой в середине пролета была подвержена динамическому воздействию в виде двух акселерограмм по двум направлениям X и Y. Результаты изображены на рисунках 2, 3 и 4.
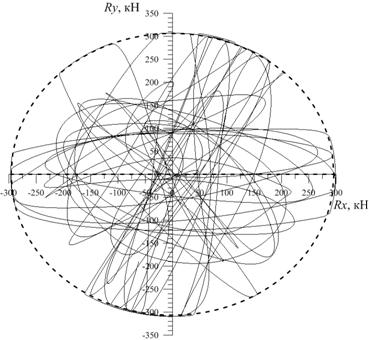
Рис. 2. Годограф изменения обобщенной реакции рамной конструкции, соответствующий решению по макромодели
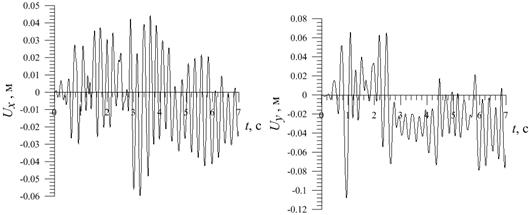
Рис. 3. Перемещения приведенной массы: (слева) по X; (справа) по Y
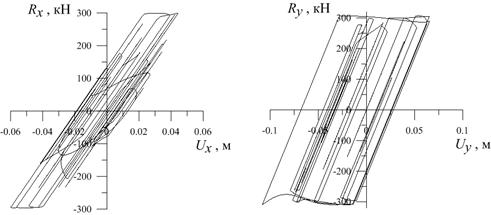
Рис. 4. График изменения обобщенной реакции системы в зависимости от перемещения, приведенной в точке массы: (слева) по X; (справа) по Y
В [2] было выполнено сравнение динамических расчетов рамных конструкций на МРЗ с использованием данной реализованной макромодели и упругопластической модели с одной степенью свободы на воздействие инструментальных акселерограмм. Также было выполнено сравнение этих результатов с результатами, полученными в ПК ANSYS, которые считались эталонными. Использование макромодели давало результаты, более близкие к эталонному решению, чем модель с одной степенью свободы.
Реализация метода макромодели в ПК MATLAB с учетом упрочнения материала конструкций
В [5] предлагается обобщение макромодели с учетом упрочнения материала конструкций. В данной статье реализована программа расчета по методу макромодели для рамных конструкций с учетом упрочнения. Программа предназначена для анализа систем с поверхностями текучести, описанными повернутым эллипсом под любым углом θ. Главной сложностью реализации такого алгоритма является учет упрочнения эллипса в виде его расширения. Для этого необходимо преобразовать условие текучести так, чтобы оно соответствовало расширяемому эллипсу, с каждым шагом решения.
В [5] поверхность
текучести, с учетом упрочнения материала конструкций, описывается уравнением ![]() . Тогда условие текучести будет
. Тогда условие текучести будет 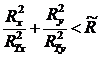 .
.
Из [5] 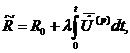 где
где ![]() –
параметр, определяющий поверхность текучести в начальный момент времени;
–
параметр, определяющий поверхность текучести в начальный момент времени; ![]() – параметр упрочнения конструкций;
– параметр упрочнения конструкций; ![]() – вектор скоростей пластических
перемещений. Из [5] имеем
– вектор скоростей пластических
перемещений. Из [5] имеем ![]()
Чтобы найти ![]() , преобразуем начальную поверхность
текучести в следующий вид:
, преобразуем начальную поверхность
текучести в следующий вид:
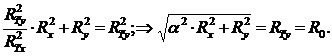 (4)
(4)
где – 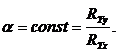
Второе слагаемое
![]() , при шаговом решении, можно вычислить
следующим образом:
, при шаговом решении, можно вычислить
следующим образом:
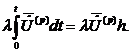 (5)
(5)
Из (4) и (5) условие текучести приобретет следующий вид:
![]() .
(6)
.
(6)
Далее стоит задача определения вектора скоростей пластических перемещений. В статье [5] скорость пластических перемещений можно вычислить из:
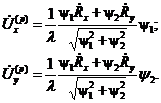 (7)
(7)
Уравнения (7) определяют скорость пластических перемещений в условиях пластической работы системы. Для общего вычисления скоростей пластических перемещений мы находим их, путем вычитания из полных скоростей, после каждого шага интегрирования скорости упругих перемещений. Тогда, в условиях упругой работы системы, скорость пластических перемещений будет равна нулю.
Как показано в [5], скорость упругих перемещений можно вычислить из:
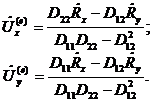 (8)
(8)
В (8) ![]() в условиях упругой работы системы
определяется по (2), а в условиях упругопластической работы системы по (3).
в условиях упругой работы системы
определяется по (2), а в условиях упругопластической работы системы по (3).
Тогда можно найти скорость пластических перемещений:
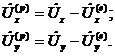 (9)
(9)
На основе вышеуказанного были реализованы алгоритм и программа расчета по методу макромодели с учетом упрочнения материала конструкций.
Интерфейс программы и также результаты тестового примера расчета рамной конструкции на максимальное расчетное землетрясение с учетом упрочнения материала показаны на рисунке 5. В области показа результатов исходная поверхность текучести изображена красным цветом, а зеленым цветом изображена поверхность после упрочнения материала конструкции. Синим цветом изображен годограф изменения обобщенной реакции R рамной конструкции.
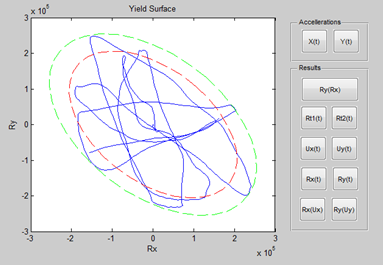
Рис. 5. Результаты тестового примера расчета рамной конструкции на МРЗ с учетом упрочнения материала
Реализация макромодели в ПК MATLAB с учетом сингулярности в поверхностях текучести рам
В целях уточнения результатов расчетов по макромодели, в [3] было выполнено обобщение метода макромодели для учета многоугольной формы и точек сингулярности в поверхностях текучести рам. В данной работе реализована программа для такого обобщения.
Особенность
создания программы расчета по методу макромодели с такими поверхностями
текучести заключалась в учете ломаного вида поверхности текучести, что означает
необходимость следить за уравнением текучести и условием разгрузки для каждого
участка. На каждом участке коэффициенты ![]() будут
разными. Вторая сложность – это учет точки сингулярности на поверхности
текучести.
будут
разными. Вторая сложность – это учет точки сингулярности на поверхности
текучести.
В данной работе была реализована программа для расчета по методу макромодели консолей с двумя степенями свободы (рис. 6а). Поверхность текучести таких конструкций имеет вид рисунка 6б.
Задача состоит в определении координат точек A, B, C и D на рисунке 6б. Из уравнений линий 1-4 (линии, отвечающие за каждый вид возможного механизма) получаем координаты всех точек сингулярности на поверхности текучести.
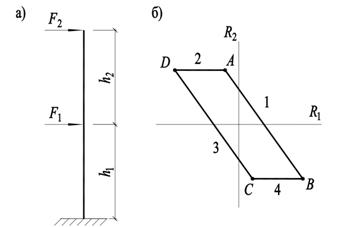
Рис. 6. Расчетная схема и поверхность текучести консоли с двумя степенями свободы
По аналогии создания этой программы можно реализовать макромодель для любых видов многоугольных поверхностей текучести.
Рецензенты:Веселов А.А., д.т.н., профессор кафедры железобетонных и каменных конструкций, ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г.Санкт-Петербург.
Кондратьева Л.Н., д.т.н., профессор, зав. кафедрой строительной механики, ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г.Санкт-Петербург.
Библиографическая ссылка
Ниджад А.Я. РЕАЛИЗАЦИЯ МЕТОДА МАКРОМОДЕЛИ ДЛЯ РАСЧЕТА РАМНЫХ КОНСТРУКЦИЙ НА МАКСИМАЛЬНОЕ РАСЧЕТНОЕ ЗЕМЛЕТРЯСЕНИЕ // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12449 (дата обращения: 13.02.2026).