Введение. На данный момент существует множество систем для создания web-приложений с SOA архитектурой [4]. В то же время эти системы не решают проблемы реализации EAI[1]. Одной из этих проблем является фактор постоянного развития сети Internet. При этом постоянное изменение архитектуры и разработка заново уже существующих интерфейсов требует непрерывной работы специалистов. В связи с этим была построена и апробирована основанная на онтологическом [3] подходе SOA-система на базе SIR-алгоритмов [2]. В онтологической SOA-системе нам потребовалось реализовать возможность использования CRUD (Сreate Read Update Delete) [6]. CRUD – сокращенное название стандартных операций при работе с хранением данных: создание, просмотр, обновление и удаление. Реализацией операции «создание» является алгоритм SIRCreate.
Рассматриваемая авторами настоящей статьи задача решена впервые с помощью применения парадигмы основанного на онтологиях доступа к данным(OBDA) [2]. Этот подход позволил использовать преимущества онтологий и технологий дескриптивных логик.
Цель работы: Продемонстрировать алгоритм SIRCreate и выявить его эффективность посредством доказательства невысокой вычислительной сложности [1] алгоритма.
Теоретические исследования. В алгоритме SIRCreate, пользуясь ранее рассмотренными алгоритмами, необходимо получить информацию из Abox [3] и обработать ее, формируя при этом конструкции для построения интерфейсов. Этот алгоритм можно использовать для операции обновления, так как при повторном запуске алгоритма на уже использованных параметрах, необходимые данные эквивалентно трансформируются без повреждения структуры системы.
Пусть К=<T, A> – база знаний логики DL-Lite𝓡[5], С, Q, S – конъюнктивные запросы[3]. На рисунке 1, представлен алгоритм SIRCreate c входными параметрами: С, S, Q, T, A.
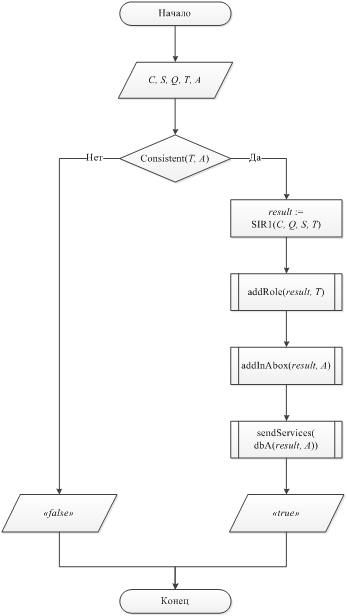
Рисунок 1. Блок-схема алгоритма SIRCreate
Функция Consistent реализует проверку базы знаний на непротиворечивость, основой этой функции является алгоритм Consistent [5]. Если база знаний оказывается противоречивой, то нет смысла проводить дальнейшие действия и алгоритм завершается.
Далее данные обрабатываются посредством алгоритма SIR1, основанного на алгоритме SIR и алгоритме RewWR. Алгоритм RewWR представляет собой модификацию алгоритма PerfectRef [5]. Модификация не использует знания о ролях (RBox) онтологии, тем самым ускоряя время обработки входных данных и уменьшая размер порождаемых запросов к базе данных. Блок-схема алгоритма RewWR представлена на рисунке 2.
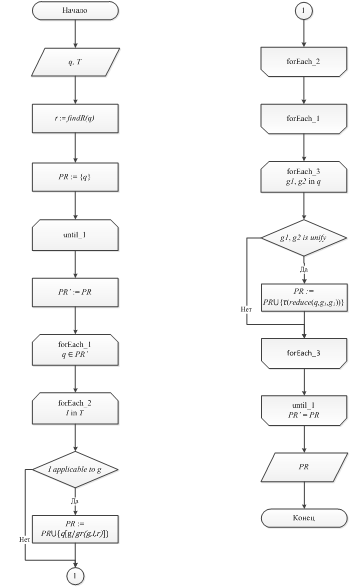
Рисунок 2. Блок-схема алгоритма RewWR
Принцип работы алгоритма состоит из следующих этапов.
1. Проверка содержания в запросе q информации о ролях.
2. Переформулировка атомов каждого соединительного запрос q ∈ PR ', и получение нового запроса для каждого атома переформулировки.
3. Вычисление соединительного запрос q' = reduce (q, g1, g2) для каждой пары атомов g1 и g2, которая унифицируется и находится в теле запроса q, Функция findR выдает результат «1» если в запросе находятся атомы с 2мя аргументами, иначе результат равен «0».
В этом алгоритме q[g/g′] - обозначает конъюнктивный запрос, полученный от q, заменой атома g новым атомом g’. Функция τ принимает в качестве входного значения конъюнктивный запрос q и возвращает новый конъюнктивный запрос, получаемый заменой каждого вхождения независимой переменной в q символом подчеркивания.
Аргумент атома в запросе является зависимым, если он соответствует распознаваемой переменной или общей переменной. Общая переменная – это константа или переменная, появляющийся, минимум, два раза в теле запроса. Аргумент атома запроса является независимым, если он является нераспознаваемой необщей переменной. Независимый аргумент атома обозначается символом подчеркивания.
Функция reduce принимает в качестве входных параметров конъюнктивный запрос q и два атома: g1 и g2, находящихся в теле запроса q, а возвращает конъюнктивный запрос q' посредством применения к q MGU(Most General Unifier)[5] между g1 и g2. При унификации g1 и g2, каждое вхождение символа «_» должно быть рассмотрено как присутствие независимой переменной. MGU заменяет каждый символ «_» в g1 на соответствующий аргумент в g2, и наоборот. Благодаря унификации, выполняемой посредством функции reduce, связанные переменные в q могут стать несвязанными в q'. Таким образом, положительные включения, которые не применимы к атомам q, позже могут стать применимыми к атомам q'.
Приведем принцип модификации функции gr.
1. Если запрос не содержит информацию о ролях, то положительное включение[5] I применимо к атому А(х), если в правой части есть I.
2. Если запрос содержит информацию о ролях, то используются способы переформулировки атомов, приведенные в функции gr для алгоритма переписывания запросов DL-Lite𝓡. Здесь положительное включение I применимо к атому P, в зависимости от наличия зависимых или независимых переменных в атоме g, или ролей в аксиомах I.
Вернемся к алгоритму SIRCreate. Процедура addRole добавляет информацию о новых интерфейсах в TBox[3] T. Процедура addInAbox добавляет информацию о новых интерфейсах в Abox А. Функция dbA выполняет запросы в триплете над Abox А, являющимся базой данных. Процедура sendServices отвечает за формирование кода с запросами под локальные выражения Abox сервисов и отправку кода по адресам клиента и сервера на основе анализа ответа глобального Abox системы.
Далее приведены леммы, необходимые для доказательства эффективности алгоритма SIRCreate.
Лемма 1. Пусть T – TBox базы знаний DL-Lite𝓡, q – коньюнктивный запрос к T. Тогда алгоритм RewWR (q, T) завершаем.
Доказательство
1. Максимальное число атомов в теле конъюнктивных запроса генерирующегося с помощью алгоритма равно длине начального запроса q. Длина запроса меньше или равна n , где n является размером запроса, т. е. n пропорциональна числу атомов и числу термов, входящих в запрос.
2. Количество термов, встречающихся в конъюнктивных запросах, сгенерированных с помощью алгоритма, равно количеству переменных и констант, входящих в q плюс символ «_». Следовательно, кардинальность такого набора меньше или равна n + 1, где n - размер запроса.
3. Число различных атомов, которые могут возникнуть в конъюнктивных запросах, генерируемых по алгоритму, меньше или равно m · (n + 1)2, m=m1+m2, где m1 – число концептов или ролей в запросе. В тоже время, m2 – число концептов или ролей в TBox или, в случае отсутствия информации о ролях в запросе, в TBox/RBox.
4. Алгоритм учитывает запросы, которые он сгенерировал.
Из пунктов 1, 2, 3 следует, что число различных соединительных запросов, сгенерированных алгоритмом, конечно. Из пункта 4 следует, что алгоритм не генерирует запрос более одного раза. Следовательно, алгоритм RewWR всегда завершается.
Лемма 2. Пусть T – TBox базы знаний DL-Lite𝓡, q – коньюнктивный запрос к T. Тогда вычислительная сложность алгоритма RewWR(q, T) находится в классе PTime[1] от размера T.
Доказательство
Число различных соединительных запросов, сгенерированных с помощью алгоритма меньше или равно (m • (n +1) 2) n и соответствует максимальному количеству выполнений цикла until_1(см. рис 2.1). Тогда m находится в линейной зависимости от размера TBox и в худшем случае, и в лучшем случае от размера TBox/RBox. В тоже время, n не зависит от размера T. Следовательно, время выполнения алгоритма RewWR полиномиально зависит от размера T.
Теорема 1. Пусть К = <T, A> - база знаний логики DL-Lite𝓡, C, Q, S – конъюнктивные запросы к T. Тогда алгоритм SIRCreate(C, Q, S, T, A) завершаем.
Доказательство
Вследствие того, что процедуры addRole, addInAbox, sendServices, функция dbA, и алгоритм Consistent завершаемы[5], доказательство следует из леммы 1.
Теорема 2. Пусть К = <T, A> - база знаний логики DL-Lite𝓡, C, Q, S –конъюнктивные запросы к T. Тогда вычислительная сложность алгоритма SIRCreate(C, Q, S, T, A) является полиномиально зависимой от размера K.
Доказательство
Вычислительная сложность алгоритма Consistent находится в классе PTime от размера TBox и в классе LogSpace[1] от размера Abox. Тогда, на основании леммы 2, можно сказать, что время выполнения алгоритма SIRCreate(C, Q, S, T, A) является полиномиально зависимым от размера К.
Заключение. Малый класс сложности алгоритма SIRCreate доказывает его эффективность. Кроме того, результаты экспериментов демонстрируют существенное уменьшение времени разработки web-ресурсов при использовании алгоритма SIR в сравнении с ручным построением сервисов.
Для реализации алгоритма рекомендуется использовать языки web-онтологий OWL и OWL 2 [2]. В частности, профиль OWL 2 QL. Для представления выходных данных рекомендуется использовать SQL-подобные языки запросов.
Апробация алгоритма проводилась на данных web-портала образовательных учреждений г. Рязани. В результате серии экспериментов зафиксировано среднее уменьшение трудоемкости создания web-сервисов на базе web-сайтов примерно на 28 %.
Рецензенты:Овечкин Г.В., д.т.н., профессор, заведующий кафедрой ВПМ Рязанского государственного радиотехнического университета, г.Рязань;
Пылькин А.Н., д.т.н., профессор, профессор кафедры ВПМ Рязанского государственного радиотехнического университета, г.Рязань;
Бабенко Л.К., д.т.н., профессор, профессор кафедры «Безопасность информационных технологий», Технологический институт Южного федерального университета, г.Ростов-на-Дону.
Библиографическая ссылка
Курдюков Н.С. ДОКАЗАТЕЛЬСТВО ЭФФЕКТИВНОСТИ АЛГОРИТМА SIRCREATE // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12427 (дата обращения: 12.03.2026).



