Для расчета многих современных технологических процессов и процессов очистки промышленных газовых выбросов в режимах с интенсивным взаимодействием фаз требуется создание математических моделей, учитывающих комплекс физических явлений межфазного обмена массой, импульсом и энергией [4-6].
Для турбулентного течения газа характерны беспорядочные хаотические пульсации скорости во всех направлениях, придающие практически всем происходящим процессам стохастический характер - отдельные объемы газа с определенной вероятностью могут перемещаться в любом направлении и истинное значение любой характеристики газа в конкретной точке в конкретный момент времени представляет собой сумму величин, характеризующих основное и пульсационное течения. Следствием хаотических пульсационных движений является беспорядочное интенсивное перемешивание и специфическая турбулентная диффузия, турбулентная вязкость газа, более равномерное, чем при ламинарном течении, распределение осредненной скорости и резкое ее падение в пристенной области, увеличение потерь на трение и т.д.
Мгновенную скорость газа в любой точке потока в каждом направлении можно представить как сумму осредненной скорости и скорости пульсаций:
wx =`wx + wx¢, wy =`wy + wy¢, wz =`wz + wz¢. (1)
Подстановка этих выражений в уравнения движения Навье-Стокса и усреднение по времени и пространству приводит к уравнениям движения Рейнольдса, в которые входят добавочные касательные напряжения, обуславливающие повышение вязкости и гидравлического сопротивления [5]. Для замыкания системы уравнений применяются статистические или полуэмпирические теории турбулентности, используется аналогия между турбулентными и молекулярными напряжениями, экспериментальные данные о статистических связях между пульсациями в пространстве и времени [3, 5, 6].
Однако использование статистической теории требует предварительных сведений о турбулентных характеристиках потока, поэтому наибольшее распространение получили статистико-феноменологические теории турбулентного переноса, в которых турбулентность характеризуется интенсивностью и масштабом или кинетической энергией пульсационного движения и скоростью ее диссипации [1, 2, 3].
Для описания процессов турбулентного переноса наряду с уравнениями осредненного турбулентного потока применяются уравнения баланса пульсационной энергии, для замыкания системы уравнений принимаются дополнительные гипотезы [5, 6]. Однако полученные таким образом модели громоздки и содержат эмпирические константы, универсальность которых строго не доказана. Поэтому для инженерных расчетов обычно используются феноменологические теории и полуэмпирические методы расчета [4-7].
Движение твердых или жидких частиц в турбулентном потоке газа отличается большей, чем в ламинарном, сложностью и интенсивностью межфазного взаимодействия. Это обусловлено, прежде всего, беспорядочными турбулентными пульсациями среды и связанными с ними колебательными движениями частиц, их турбулентной диффузией. Можно считать, что движение частиц в турбулентном газовом потоке складывается из поступательного движения под действием внешних сил и сил, связанных с их обтеканием, и хаотического движения под влиянием турбулентных пульсаций газа [5-9]. В восходящем или нисходящем потоке можно считать, что на частицу кроме силы сопротивления действует только сила тяжести и уравнение поступательного движения частицы при стоксовском режиме обтекания можно записать в виде [5, 6]
![]() , (2)
, (2)
которое допускает аналитическое решение в виде [5, 6]
u = w ± gt + C×exp(-t/t), (3)
где u – скорость частицы, м/с; w – скорость газа, м/с; t = d2rd/(18m) – время релаксации скорости частицы, с; C – константа интегрирования; d – диаметр частицы, м; rd и r – плотности частиц и газа, кг/м3; g – ускорение свободного падения (знак «+» относится к нисходящему потоку, «-» - к восходящему), м/с2; r – радиус-вектор (расстояние от оси канала), м.
Если при t = 0 u = u0, то в уравнении (3) C = u0 - w ± gt, тогда
u = w - (w - u0)exp(-t/t) ± gt×[1 - exp(-t/t)] (4)
Легко видеть, что при t >> t (реально при t > 5t) скорость относительного движения v = w - u принимает постоянное максимальное предельное значение v = gt (для восходящего потока u = w - gt, для нисходящего u = w + gt). Обычные значения времени релаксации частиц диаметром от 0,1 до 100 мкм лежат в пределах от 10-8 до 10-2 с, значение предельной скорости относительного движения частиц в осевом направлении - в пределах от 10-7 до 0,1 м/с, что значительно меньше обычных скоростей газа, поэтому осевая скорость мелких частиц часто принимается равной скорости газа [1-3]. Кроме того, в большинстве практически значимых случаев с некоторой погрешностью при t ³ t можно считать движение частицы безинерционным и существенно упростить нестационарные модели за счет замены дифференциальных уравнений алгебраическими [1-6].
Наличие градиента осевой скорости газа в турбулентном потоке приводит к появлению специфической формы продольного движения частиц, в результате чего их относительная скорость меняет по сечению канала не только свое значение, но и направление. В общем случае в ядре потока локальные скорости частиц могут быть выше скорости газа, а в периферийной области - ниже, причем средняя по сечению скорость частиц может быть меньше средней скорости газа на 1,5-2 м/с для высокодисперсных и на 8-10 м/с для крупных частиц [5]. Отставание частиц дисперсной фазы от сплошной не всегда удается объяснить влиянием силы тяжести, так как, во-первых, оно характерно и для высокодисперсных частиц и, во-вторых, аналогичная картина наблюдается при течении двухфазных систем в горизонтальных каналах [10]. Определенное влияние на величину продольного скольжения частиц оказывают и взаимодействие частиц друг с другом и со стенками канала, однако основную роль, видимо, играют процессы, связанные с перераспределением частиц с разной скоростью по сечению канала, - турбулентная диффузия, подъемная и турбулентная поперечная миграция [1-3].
Градиент продольной скорости газа приводит к вращению частицы вокруг своей оси и ее поперечному движению, причиной которого является сила Магнуса-Жуковского, направленная перпендикулярно вектору относительной скорости в сторону максимального значения суммы тангенциальных составляющих скоростей обтекания и вращения (рис. 1) [2]:
![]() (5)
(5)
где W – угловая скорость вращения частицы, с-1; v – вектор скорости относительного движения частицы, м/с.
а) 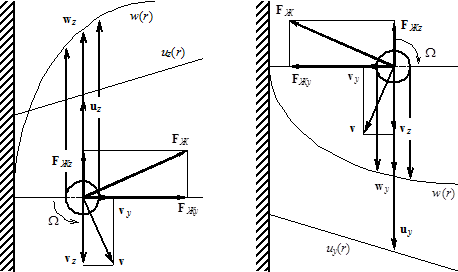 б)
б)
Рис. 1. Схема возникновения подъемной силы в восходящем (а) и нисходящем (б) потоках
Тогда на частицу кроме сил, связанных с ее обтеканием, и силы тяжести (с учетом силы Архимеда) действует поперечная сила Магнуса-Жуковского, возникающая при вращении частицы вокруг собственной оси из-за градиента скорости газа, и уравнение ее движения в векторной форме можно записать в виде [5,6]:
![]() (6)
(6)
где u – вектор скорости частицы, FЖ, FС, G и FА – векторы сил Магнуса-Жуковского, сопротивления, тяжести и Архимеда.
При анализе движения частиц в осесимметричном канале сделаем следующие допущения: течение газа установившееся адиабатическое; радиальная составляющая скорости газа отсутствует; частицы сохраняют сферическую форму; взаимодействие между частицами отсутствует. Тогда система уравнений двухмерного нисходящего или восходящего движения частицы в газовом потоке в проекциях на оси координат (ось z направлена по оси канала) может быть записана в виде [5, 6]:
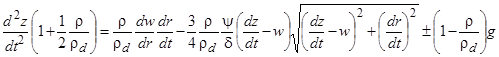 , (7)
, (7)
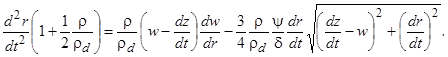 (8)
(8)
Левые части уравнений (7) и (8) отражают влияние сил инерции частиц и эффект «присоединенной массы» (силу Тейлора) - влияние сил инерции массы газа, двигающейся вместе с частицей [1-3]. В правых частях уравнений первые слагаемые отражают влияние силы Магнуса-Жуковского, вторые - силу лобового аэродинамического сопротивления, третье слагаемое в уравнении (7) отражает совместное влияние сил тяжести и Архимеда.
Система дифференциальных уравнений (7)-(8) в общем виде при заданных начальных условиях в общем виде может быть решена только численными методами. На рисунках 2 и 3 представлены некоторые результаты численного решения для восходящего и нисходящего двухфазных потоков.
Из анализа результатов расчетов в широких интервалах изменения основных параметров можно сделать следующие выводы [5, 6]:
-
в восходящем потоке частицы под действием градиента осевой скорости в целом перемещаются к оси канала, в нисходящем – к стенке;
-
при обычных значениях основных параметров относительная осевая скорость частиц быстро становится равной скорости седиментации, и для оценочных расчетов при нисходящем и восходящем течении можно, соответственно, принимать uz » w ± vs;
- подъемная сила Магнуса-Жуковского при обычных значениях основных параметров потока может оказывать существенное влияние на движение только достаточно крупных частиц с размерами более 50¸100 мкм с небольшими начальными скоростями и в пределах ламинарного пристенного и буферного слоя.
Полученные результаты расчетов подтверждаются данными экспериментальных исследований [5-7]. Отклонения траекторий частиц от расчетных (равновесных) в реальных условиях могут быть вызваны, в первую очередь, турбулентными пульсациями газа и, кроме того, регенерацией свободной поверхности частиц или капель за счет их взаимодействия с поверхностью канала (осаждение и унос) или между собой (коагуляция), а также дробления [5, 6]. Поэтому расчетные зависимости и траектории частиц в турбулентном газодисперсном потоке можно рассматривать только как осредненные или как тенденции поведения частиц. В турбулентных потоках, в которых траектории частиц определяются не только детерминированными силами, но и случайными воздействиями турбулентных пульсаций газа, это явление проявляется только как общая тенденция и только на больших расстояниях от входа.
Разработанная методика и результаты расчетов могут использоваться для моделирования турбулентных газодисперсных потоков, расчета концентраций дисперсной фазы в потоке, технологической и социально-экологической эффективности процессов очистки отходящих промышленных газов от пыли [4-9].
а) б)
б)
Рис. 2. Равновесные траектории частиц (капель воды) в вертикальном восходящем потоке при скорости газа 10 м/с (а) и 50 м/с (б):
1 - d = 20 мкм; 2 - 50; 3 - 100; 4 - 200; 5 - 500; 6 - 1000;
D = 50 мм, при t = 0 z = 0, y0 = 0, r = r0, u0 = 0, dz/dt = uz0, dr/dt = ur0.
а)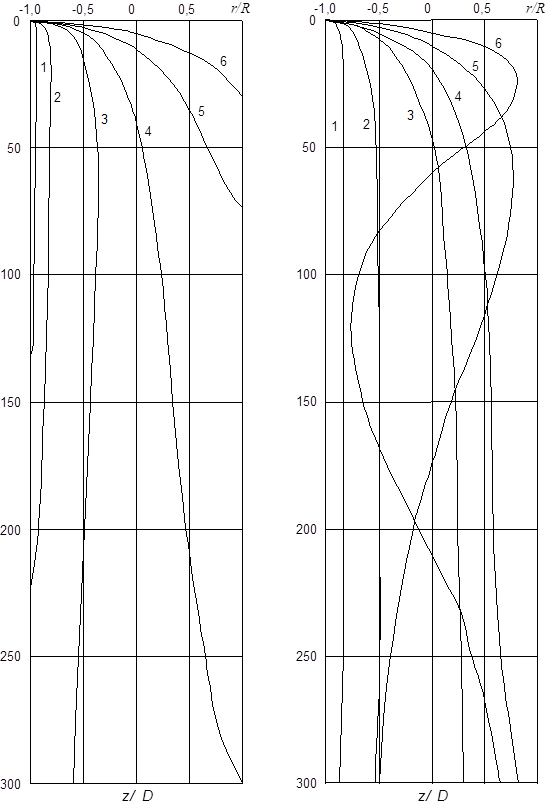 б)
б)
Рис. 3. Равновесные траектории частиц (капель воды) в вертикальном нисходящем потоке при скорости газа 10 м/с (а) и 50 м/с (б):
1 - d = 50 мкм; 2 - 100; 3 - 200; 4 - 300; 5 - 500; 6 - 1000;
воздух-вода, D = 50 мм, при t = 0 z = 0, y0 = 0, r = r0, u0 = 0, dz/dt = uz0, dr/dt = ur0.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект 14-06-00256) и Министерства образования и науки Российской Федерации.
Рецензенты:
Чекалов Л.В., д.т.н., генеральный директор ЗАО «Кондор-Эко», Ярославская область, п. Семибратово.
Войнов Н.А., д.т.н., профессор, Сибирский государственный технологический университет, г. Красноярск.
Библиографическая ссылка
Сугак А.В., Сугак Е.В. РАВНОВЕСНЫЕ ТРАЕКТОРИИ ЧАСТИЦ В ТУРБУЛЕНТНОМ ПОТОКЕ ГАЗА // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12336 (дата обращения: 13.02.2026).



