Введение. Современные производственные системы являются сложными техническими объектами, часто имеющими нелинейную динамическую структуру. Для их исследования необходимо создание математических моделей и алгоритмов, ориентированных на применение современных средств вычислительной техники. В связи с этим актуальными являются вопросы, связанные с разработкой методов идентификации нелинейных динамических объектов. При этом необходимо рассмотрение всей имеющейся априорной информации при построении моделей процесса, что достигается за счет применения современных методов параметрической и непараметрической идентификации.
Наиболее важным с точки зрения приложений классом динамических процессов являются системы типа «вход – выход», представимые в виде черного ящика, допускающие активный эксперимент при отсутствии полной априорной информации о моделируемом объекте. Настоящая работа посвящена рассмотрению задачи идентификации динамических систем «в широком смысле», то есть в условиях, когда параметризация невозможна или удается частично параметризовать модель исследуемого процесса на основании имеющейся априорной информации.
Рассматривается задача идентификации нелинейных динамических систем, представленных в виде последовательного соединения линейного динамического и нелинейного статического блоков (модель Винера), линейная динамическая часть которых находится в условиях непараметрической неопределенности. Вид нелинейности предполагается известным с точностью до параметров. Целью работы является повышение эффективности моделирования нелинейных динамических объектов в условиях малой априорной информации. Таким образом, исследуется задача моделирования нелинейных динамических процессов, находящихся в условиях частичной параметризации.
Постановка задачи. Рассматривается задача идентификации динамических систем класса Винера в условиях частичной параметризации. Пусть исследуемый объект может быть описан как последовательное сочетание линейных динамических и нелинейных статических блоков (модель Винера). Линейный динамический блок модели воспроизводит динамические свойства исследуемого объекта, нелинейный блок – имитирует его нелинейные свойства [5]. Сложность в построении моделей таких объектов заключается в том, что значения промежуточных сигналов (значения выхода блока, находящегося первым в последовательности) недоступны для измерения.
Задача идентификации нелинейной динамической системы поясняется на Рисунке 1:
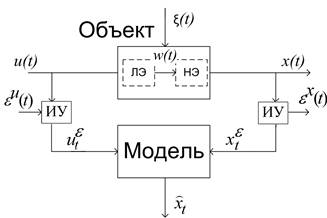
Рисунок 1. Постановка задачи идентификации
где Объект – система, состоящая из ЛЭ – линейной динамической и НЭ – нелинейной статической частей, ИУ – измерительное устройство, u(t) – входная переменная объекта, x(t) – выходная переменная, ![]() или {ui,xi, t=1,s} – наблюдения переменных процесса в дискретный момент времени, ξ(t) – ненаблюдаемое случайное воздействие,
или {ui,xi, t=1,s} – наблюдения переменных процесса в дискретный момент времени, ξ(t) – ненаблюдаемое случайное воздействие, ![]() – случайные факторы, действующие в каналах измерения переменных в дискретные моменты времени t,
– случайные факторы, действующие в каналах измерения переменных в дискретные моменты времени t, ![]() – выход модели объекта.
– выход модели объекта.
Исходные данные о состоянии исследуемого объекта представляют собой выборку измерений реакции объекта на входное воздействие u(t): ![]() . Параметры и порядок дифференциального уравнения, которым может быть описана линейная динамическая часть системы, неизвестны. Пусть нелинейность в объекте описывается функцией, вид которой предполагается известным с точностью до набора параметров. Рассмотрим системы, в которых нелинейный элемент представляет собой квадратор:
. Параметры и порядок дифференциального уравнения, которым может быть описана линейная динамическая часть системы, неизвестны. Пусть нелинейность в объекте описывается функцией, вид которой предполагается известным с точностью до набора параметров. Рассмотрим системы, в которых нелинейный элемент представляет собой квадратор: ![]() , или звено насыщения (с порогом насыщения b1):
, или звено насыщения (с порогом насыщения b1): 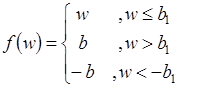 .
.
Требуется на основании имеющейся информации построить модель данной системы, адекватно описывающую ее поведение при подаче на ее вход воздействий различного вида.
Непараметрическая модель системы типа Винера. Будем исследовать системы, которые могут быть представлены в виде модели Винера [2] (Рисунок 1). Пусть порядок и параметры линейной динамической части модели Винера неизвестны, а структура нелинейного элемента задана с точностью до набора параметров α. Основная идея алгоритма, предлагаемого для построения моделей таких систем, заключается в использовании непараметрических оценок для описания связей системы, информация о которых по каким-то причинам неизвестна (в данном случае измерению недоступна линейная динамическая часть системы), а также в применении непараметрического подхода к оцениванию функций.
Как видно из рисунка, значение выхода исследуемого объекта вычисляется как некоторая функция от значения w(t):
![]() , (1)
, (1)
где x(t) – выходной сигнал системы; w(t) – выход линейной части системы (не измеряемый); u(t) – входной сигнал системы; f{w(t),α} – нелинейный оператор.
Предположим, что выход w(t) может быть измерен, тогда модель линейного динамического звена системы при входном воздействии u(t) может быть оценена как интеграл Дюамеля, то есть:
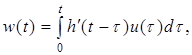 (2)
(2)
где h(t) – переходная характеристика системы, t – переменная интегрирования.
Тогда в соответствии с (1) модель исследуемого объекта:
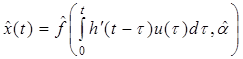 (3)
(3)
Математическая модель нелинейного объекта может быть представлена в виде системы (3), где вместо переходной функции h(t) и параметров a используются их статистические оценки.
Значение переходной функции h(t) представляет собой реакцию линейного динамического элемента системы на подачу на ее вход воздействия u(t)=1, то есть h(t)=w(t/u(t)=1). При этом значение w(t) недоступно для измерения. После подачи на вход единичного воздействия возможно измерить только выход нелинейного объекта х(t), который будет иметь значение, равное х(t)=f(h(t)).
Тогда значения переходной функции линейного элемента системы в дискретные моменты времени могут быть оценены следующим образом:
![]() (4)
(4)
где ![]() – экспериментально полученные значения выхода исследуемого объекта при подаче на вход единичного ступенчатого воздействия 1(t),
– экспериментально полученные значения выхода исследуемого объекта при подаче на вход единичного ступенчатого воздействия 1(t), ![]() – рассчитанное значение переходной характеристики линейного элемента системы. Алгоритмы оценивания неизвестной функции f -1(x) и ее параметров α зависят от типа нелинейности в объекте и будут приведены далее.
– рассчитанное значение переходной характеристики линейного элемента системы. Алгоритмы оценивания неизвестной функции f -1(x) и ее параметров α зависят от типа нелинейности в объекте и будут приведены далее.
Далее на основании выборки дискретных значений можно оценить переходную функцию системы в виде стохастической аппроксимации регрессии непараметрического типа следующим образом [4]:
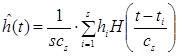 , (5)
, (5)
При этом колоколообразная функция ![]() и параметр размытости
и параметр размытости ![]() должны удовлетворять условиям сходимости [4]:
должны удовлетворять условиям сходимости [4]:
![]() , (6)
, (6)
![]()
![]() (7)
(7)
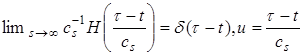 .
.
В этом случае непараметрическая оценка весовой функции, которая является производной по времени от переходной, примет следующий вид:
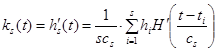 , (8)
, (8)
Подставив оценку весовой функции в интеграл Дюамеля в соответствии с (2), получим непараметрическую модель, оценивающую выход линейного элемента [3]:
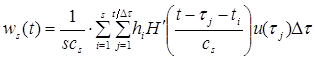 , (9)
, (9)
где τ – переменная интегрирования, ![]() – шаг дискретизации.
– шаг дискретизации.
Тогда непараметрическая модель нелинейного объекта примет вид [7]:
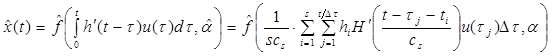 (10)
(10)
где x(t) – выходной сигнал системы; u(t) – входной сигнал системы; f{w(t),α} – оценка нелинейной функции, ![]() – оценки параметров нелинейного элемента системы,
– оценки параметров нелинейного элемента системы, ![]() – оценка переходной функции линейного элемента системы.
– оценка переходной функции линейного элемента системы.
Идентификация нелинейной системы с квадратором. Пусть имеем систему, представленную в виде модели Винера (рисунок 2). Причем нелинейная часть системы представляет собой квадратор, описываемый функцией вида: ![]() , где a=const. Выход объекта вычисляется следующим образом:
, где a=const. Выход объекта вычисляется следующим образом: ![]() . При единичном входном воздействии
. При единичном входном воздействии ![]() выход нелинейной системы равен
выход нелинейной системы равен ![]() . То есть оценку значений переходной характеристики линейного элемента
. То есть оценку значений переходной характеристики линейного элемента ![]() можно рассчитать через выход исследуемого процесса следующим образом:
можно рассчитать через выход исследуемого процесса следующим образом: ![]() , где х1i – выход исследуемой системы при единичном входном воздействии в момент времени t [2].
, где х1i – выход исследуемой системы при единичном входном воздействии в момент времени t [2].
Далее оцениваем переходную характеристику системы с применением непараметрического метода следующим образом:
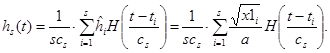 (12)
(12)
При произвольном входном воздействии и нулевых начальных условиях выход линейной части системы описывается интегралом Дюамеля (8). С учетом рассчитанного значения переходной функции (16) выход линейного элемента равен:
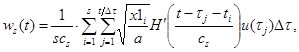 (13)
(13)
где а – неизвестная константа (параметр нелинейного элемента системы).
Таким образом, модель нелинейного динамического объекта типа Винера имеет вид:
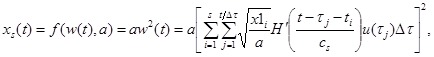 (14)
(14)
Расчетная формула для оценки выхода нелинейной системы при произвольном входном воздействии примет следующий вид:
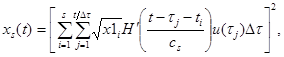 (15)
(15)
где x1i – реакция нелинейной системы на единичное входное воздействие, u(t) – входное воздействие. Таким образом, получается методика, для реализации которой не требуется точное численное значение параметра квадратора.
Пример. Рассмотрим нелинейную динамическую систему, состоящую из квадратора (параметр а=2) и разностного аналога дифференциального уравнения (имитирующего объект): ![]() . Предполагаем, что вид и параметры реального уравнения, описывающего процесс, неизвестны. Результат моделирования такого процесса представлен на рисунке 3.
. Предполагаем, что вид и параметры реального уравнения, описывающего процесс, неизвестны. Результат моделирования такого процесса представлен на рисунке 3.
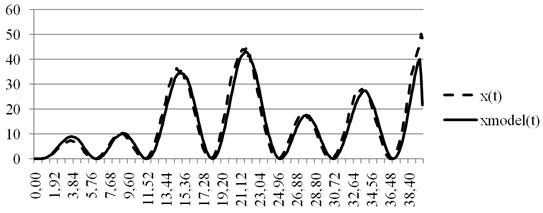
Рисунок 3. Результат оценки выхода х(t). xmodel(t) – модель нелинейной системы, x – выход системы, объем выборки s=250, h=0.16, помеха 5 %, входное воздействие: u(t)=3cos(0.5t)+sin(0.2t), относительная ошибка моделирования 3.7 %
Анализируя результаты моделирования, можно сказать, что предлагаемые алгоритмы позволяют достаточно точно оценивать значения выхода исследуемой системы при различных значениях параметров нелинейной части объекта, в условиях зашумленности каналов связи, при различных входных воздействиях.
Идентификация нелинейной системы с насыщением. Пусть нелинейное звено системы описывается функцией вида (2). В данном случае при w(t)<b выход объекта совпадает с выходом его линейной динамической части. В остальных случаях выход объекта представляет собой константу, которую возможно определить опытным путем в результате нескольких статических экспериментов, описанных далее [1].
1. Проводится серия экспериментов, в ходе которых будем подавать на вход системы воздействия различной амплитуды ![]() ,
, ![]() , в результате получим выборку
, в результате получим выборку ![]() , на основании которой делается вывод о нелинейности.
, на основании которой делается вывод о нелинейности.
2. В результате получается оценка нелинейного элемента системы, параметры которого определяются следующим образом:
- находится расстояние между двумя соседними измерениями: ![]() , где h – шаг дискретизации;
, где h – шаг дискретизации;
- оценка порога нелинейности ![]() , если
, если ![]() ;
;
- ![]() , где
, где ![]() , и
, и ![]() .
.
3. На вход объекта подается ступенчатая функция, амплитуда которой не превышает значение порога b – в результате получаем переходную характеристику и строим модель линейной части объекта в виде интеграла Дюамеля.
4. Строится модель объекта, выход которой равен значению функции, описывающей нелинейное звено, аргументом которой является выход модели линейной части объекта.
Рассмотрим нелинейную динамическую систему, состоящую из звена насыщения вида (2) (параметры b=0.75, b1=1) и разностного аналога дифференциального уравнения (имитирующего объект): ![]() .
.
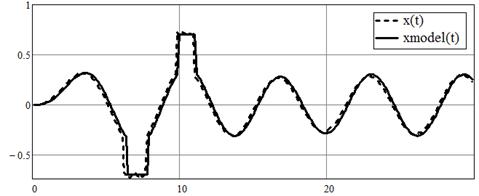
Рисунок 4. Результаты оценки выхода x(t), xmodel(t) – модель нелинейной системы, x(t) – выход системы, объем выборки s=200, шаг дискретизации h=0.15, помеха 5 %, входное воздействие u(t)=0.35sin(t), средняя ошибка моделирования 2 %
Делая анализ работы модели нелинейного динамического объекта с видом нелинейности типа звено насыщения и квадратор, можно сделать выводы о том, что непараметрическая модель достаточно точно описывает систему при различных значениях параметров нелинейной части объекта, в условиях зашумленности каналов связи, при различном объеме выборки и различных входных воздействиях.
Заключение. В статье рассмотрена задача идентификации нелинейных динамических систем, представимых в виде моделей Винера. Исследуются системы, находящиеся в условиях частичной параметризации. В данном случае структура линейного динамического блока неизвестна, а вид нелинейности предполагается известным с точностью до параметров.
Задача идентификации нелинейной системы рассмотренного типа может быть разделена на две части. Сначала рассматривается непараметрическая идентификация линейного элемента, алгоритм которой связан с тем, что реакция линейной системы на входное воздействие описывается интегралом Дюамеля. Суть метода заключается в построении моделей и получении прогноза выхода нелинейных динамических систем посредством сочетания моделей линейного динамического и нелинейного статического процессов в общей модели системы. Данный метод не предусматривает наличия полной априорной информации о структуре объекта.
Показана работоспособность предлагаемого алгоритма и применимость к задаче построения нелинейных динамических систем типа Винера в различных условиях, что расширяет область применения непараметрических методов к новым объектам исследования, а также закладывают теоретическую основу для дальнейшего проектирования. Описанные методы построения и исследования моделей позволяют производить моделирование технологических процессов и систем, имеющих нелинейную структуру.
Рецензенты:
Охорзин В.А., д.т.н., профессор, профессор кафедры Прикладной математики Сибирского государственного аэрокосмического университета «Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева», г. Красноярск.
Демиденко Н.Д., д.т.н., профессор, ведущий научный сотрудник СКТБ «Наука» КНЦ CO РАН, Федеральное государственное бюджетное учреждение науки Специальное конструкторско-технологическое бюро «Наука» Красноярского научного центра Сибирского отделения Российской академии наук, г. Красноярск.
Библиографическая ссылка
Коплярова Н.В. НЕПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ СИСТЕМ КЛАССА ВИНЕРА // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12309 (дата обращения: 13.02.2026).



