Введение
Основы теории оптимального приема хорошо известны в радиотехнике и используются при приеме и обработке сигналов. Они достаточно подробно изложены в ряде работ [2, 3, 5] и позволяют оптимизировать обработку данных во многих практических приложениях при решении задач обнаружения сигнала, оценки параметров, разрешения подобных сигналов. В настоящей работе рассматривается возможность применения основ теории оптимального приема к обработке спектральных линий отдельных атомов, получаемых с помощью дифракционной решетки. Теория дифракции света от отдельных атомов на дифракционной решетке хорошо известна из классических учебников [4]. Спектральные максимумы позволяют получить информацию о длинах волн света, излучаемого атомами, интенсивности излучения. Совокупность спектральных линий уникальна для каждого атома и позволяет обнаруживать и идентифицировать химические элементы методом спектрального анализа. В настоящей работе разрабатывается методика цифровой обработки данных, получаемых с помощью дифракционной решетки, определяются потенциально достижимые точности оценки параметров, и проводится анализ особенностей обработки данных.
На дифракционную решетку падает световой поток с определенными параметрами. Этот поток в дифракционной решетке преобразуется в угловой спектр. Вследствие линейности преобразования к новому объекту – спектру дифракционной решетки вполне возможно применение основных положений теории оптимального приема. Однако следует уточнить терминологию. В качестве сигнала будем рассматривать отдельную линию спектра или совокупность спектральных линий. Параметрами сигнала являются: длина волны, угловое положение спектральной линии, амплитуда (интенсивность света в максимуме спектральной линии). Дополнительными параметрами сигнала являются параметры дифракционной решетки: ширина щели, период, количество щелей. Принятым сообщением является сигнал (спектральная линия) с аддитивным шумом, имеющим нормальное распределение с нулевым средним значением, дисперсией![]() и интервалом корреляции
и интервалом корреляции![]() . Аддитивный шум представляет собой угловой спектр случайного потока света, падающего на дифракционную решетку. В качестве энергии сигнала будем использовать известное выражение в радиотехнике, представляющее интеграл по углам дифракции от квадрата модуля сигнала. В настоящей работе представлены результаты исследований возможностей цифровой обработки отдельной линии спектра, с помощью модельных расчетов.
. Аддитивный шум представляет собой угловой спектр случайного потока света, падающего на дифракционную решетку. В качестве энергии сигнала будем использовать известное выражение в радиотехнике, представляющее интеграл по углам дифракции от квадрата модуля сигнала. В настоящей работе представлены результаты исследований возможностей цифровой обработки отдельной линии спектра, с помощью модельных расчетов.
Основы теории
Запишем амплитуду света ![]() , прошедшего через дифракционную решетку в направлении
, прошедшего через дифракционную решетку в направлении ![]() , в виде:
, в виде:
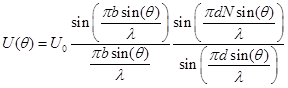 ,1
,1
где ![]() – амплитуда сигнала;
– амплитуда сигнала;
![]() – ширина щели;
– ширина щели; ![]() – период дифракционной решетки;
– период дифракционной решетки; ![]() – количество щелей дифракционной решетки;
– количество щелей дифракционной решетки;![]() – длина волны.
– длина волны.
В точках ![]() выражение (1) определяет максимумы спектральных линий. Выделим спектральную линию первого порядка с номером
выражение (1) определяет максимумы спектральных линий. Выделим спектральную линию первого порядка с номером ![]() и запишем для нее аналитическое выражение в окрестности
и запишем для нее аналитическое выражение в окрестности ![]() в виде:
в виде:
![]() ,2
,2
где ![]() – вектор параметров сигнала;
– вектор параметров сигнала;
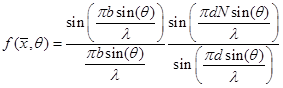
Принятое сообщение будет иметь вид:
![]() 3
3
На основании (3) запишем, согласно положениям теории оптимального приема [1, 2, 3], логарифм функции правдоподобия:
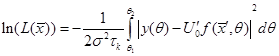 4
4
![]() – пределы интегрирования справа и слева от максимума спектральной линии. Штрихами отмечены оценочные параметры спектральной линии.
– пределы интегрирования справа и слева от максимума спектральной линии. Штрихами отмечены оценочные параметры спектральной линии.
Функция правдоподобия является условной плотностью распределения вектора параметров спектральной линии. Максимум этой функции определяет наиболее вероятные оценочные параметры сигнала. Следовательно, дифференцируя (4) по параметрам и приравнивая дифференциалы нулю, можно получить уравнения правдоподобия, решения которых дают оценку параметров сигнала. Пусть неизвестным параметром сигнала является его амплитуда![]() . Дифференцируя (4) по
. Дифференцируя (4) по ![]() и приравнивая дифференциал к нулю, можно получить решение:
и приравнивая дифференциал к нулю, можно получить решение:
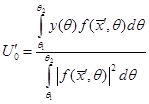 5
5
Решение имеет интегральный характер. Оно учитывает всю информацию об амплитуде в принятом сообщении. Математическое ожидание от оценочной амплитуды ![]() равно истинной амплитуде
равно истинной амплитуде ![]() . Решение (5) является несмещенным.
. Решение (5) является несмещенным.
![]()
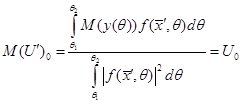 6
6
Оценим дисперсию амплитуды![]() в точке
в точке ![]() . Для этого, согласно положениям теории оптимального приема [2, 3] определим элемент информационной матрицы Фишера по выражению:
. Для этого, согласно положениям теории оптимального приема [2, 3] определим элемент информационной матрицы Фишера по выражению:
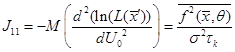 7
7
Черта сверху означает интегрирование по![]() .
.
Обратное значение определяет дисперсию оценочной амплитуды ![]() дисперсию Рао –Крамера):
дисперсию Рао –Крамера):
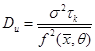 8
8
Дифракционная решетка является фильтром, преобразующим световой поток в угловой спектр. В связи с этим шумовая составляющая на выходе фильтра будет иметь интервал корреляции ![]() .
.
С другой стороны, ![]() в пределах спектральной линии может быть оценена значением
в пределах спектральной линии может быть оценена значением ![]() . Следовательно, дисперсия амплитуды практически равна дисперсии шума. Дифракционная решетка, реализующая угловой спектральный анализ, является оптимальным фильтром, максимизирующим отношение сигнал / шум. Дальнейшая обработка принятого сообщения методом максимального правдоподобия не увеличивает отношения сигнал / шум.
. Следовательно, дисперсия амплитуды практически равна дисперсии шума. Дифракционная решетка, реализующая угловой спектральный анализ, является оптимальным фильтром, максимизирующим отношение сигнал / шум. Дальнейшая обработка принятого сообщения методом максимального правдоподобия не увеличивает отношения сигнал / шум.
Подставим выражение для оценочной амплитуды (5) в функционал правдоподобия и преобразуем его:
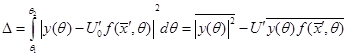 9
9
Черта сверху означает интегрирование. В результате получим оценку качества обработки. По своему содержанию значение поверхности функционала в минимуме определяет дисперсию шума. Следовательно, метод максимального правдоподобия может дать оценку дисперсии шума при обработке принятого сообщения по значению минимума функционала правдоподобия.
Решение (5) получено при интегрировании всей принятой реализации. Оно имеет максимальную точность. Однако можно выделить отдельный фрагмент принятой реализации, например область максимума. В этом случае определяется амплитуда этого фрагмента (области максимума) и его положение на принятой реализации. Если выделенный фрагмент вырождается в значение функции в точке, тогда обработка является точечной. Ее практически используют для оценки углового положения максимума. Приведем основные выражения для оценки максимума линии спектра дифракционной решетки и его углового положения на принятой реализации. Примем размер фрагмента, равным ширине спектральной линии:
![]() 10
10
В этом случае энергия сигнала за счет уменьшения пределов интегрирования будет меньше:
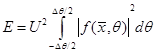 11
11
Записывая логарифм функции правдоподобия, выполняя операцию дифференцирования и приравнивая дифференциал нулю, можно получить решение. Оно отличается от решения (5) лишь пределами интегрирования.
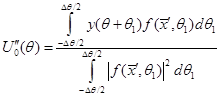 12
12
Решение (12) представляет собой процесс фильтрации корреляционным фильтром. Импульсной характеристикой этого фильтра является функция от ![]() с энергией, равной единице:
с энергией, равной единице:
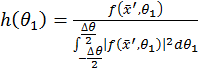 13
13
Результаты модельных исследований
В модельных расчетах принято следующее. Длина волны света равна ![]() м. Она соответствует красной линии атома водорода. Амплитуда света равна единице, угол падения равен нулю. Ширина щели дифракционной решетки
м. Она соответствует красной линии атома водорода. Амплитуда света равна единице, угол падения равен нулю. Ширина щели дифракционной решетки ![]() м, период решетки
м, период решетки ![]() м, интервал дискретизации
м, интервал дискретизации ![]() радиан, количество щелей
радиан, количество щелей ![]() . В качестве шума принят аддитивный нормальный шум с дисперсией
. В качестве шума принят аддитивный нормальный шум с дисперсией ![]() , средним значением, равным нулю, и интервалом корреляции
, средним значением, равным нулю, и интервалом корреляции ![]() . На рис. 1 показан вид красной линии спектра атома водорода первого порядка.
. На рис. 1 показан вид красной линии спектра атома водорода первого порядка.
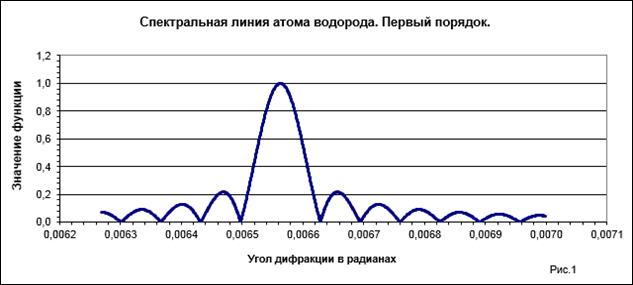
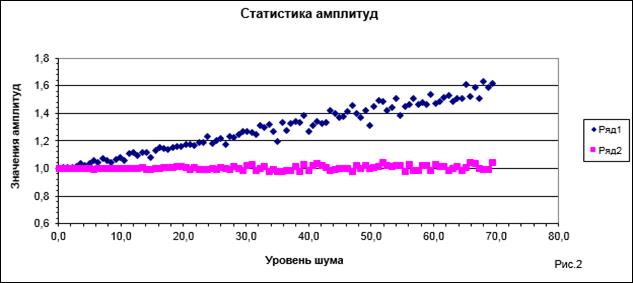
На рис. 2 показана статистика амплитуд, определенная при различных реализациях шума. Сравниваются статистики двух решений. Первое решение (ряд 1) находится по максимуму линии спектра (традиционное решение). Второе решение получено методом максимального правдоподобия (выражение 12) при учете 300 значений в окрестности максимума линии спектра (ряд 2). Из рисунка ясно, что интегральное решение (ряд 2) обеспечивает большую точность оценки амплитуды (![]() ). Традиционное решение по максимуму спектральной линии имеет смещение, обусловленное тем, что при нахождении максимума учитывается всегда положительное значение шума. В результате статистика амплитуды изменяется и при увеличении уровня шума смешение решения увеличивается. По горизонтали отложен уровень шума. Он связан со среднеквадратичным значением шума (СКО) линейной зависимостью (рис. 3).
). Традиционное решение по максимуму спектральной линии имеет смещение, обусловленное тем, что при нахождении максимума учитывается всегда положительное значение шума. В результате статистика амплитуды изменяется и при увеличении уровня шума смешение решения увеличивается. По горизонтали отложен уровень шума. Он связан со среднеквадратичным значением шума (СКО) линейной зависимостью (рис. 3).
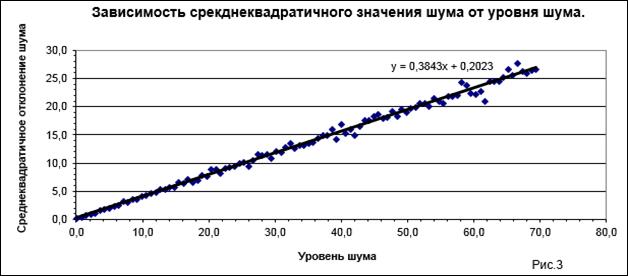
На рис. 4 приведены статистики углов дифракции, определяющих максимум линии спектра![]() . Статистика также получена для двух случаев решения: по максимуму линии спектра (ряд 1) и методом максимального правдоподобия (ряд 2, интегральное решение).
. Статистика также получена для двух случаев решения: по максимуму линии спектра (ряд 1) и методом максимального правдоподобия (ряд 2, интегральное решение).
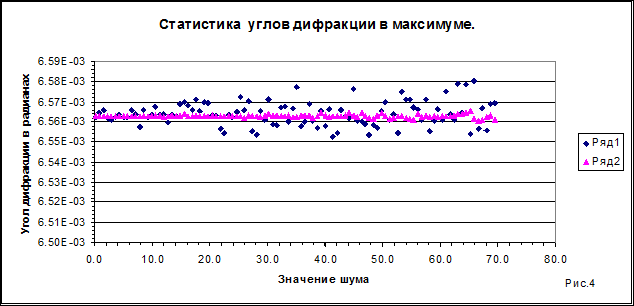
Интегральное решение дает большую точность оценки ![]() , а, следовательно, и оценки длины волны
, а, следовательно, и оценки длины волны ![]() . На рис. 5 показана зависимость энергии сигнала от ширины фрагмента.
. На рис. 5 показана зависимость энергии сигнала от ширины фрагмента.
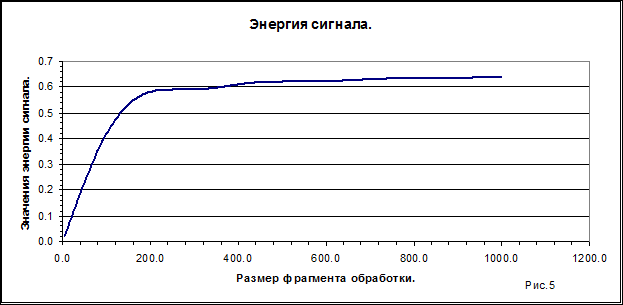
Из рисунка ясно, что практически вся энергия сосредоточена в окрестности максимума, шириной ~300 отсчетов (![]() радиан). Ширина спектрального максимума равна
радиан). Ширина спектрального максимума равна ![]() радиан.
радиан.
На рис. 6 показана статистикауглов дифракции при максимуме спектральной линии в зависимости от размера фрагмента обработки. Уровень шума постоянен и равен 40 (средне квадратичное значение ![]() ). Как видно из рисунка, при количестве точек более 200 точность оценок стабилизируется и в дальнейшем изменяется слабо. Аналогичная особенность отмечается и в статистике амплитуд.
). Как видно из рисунка, при количестве точек более 200 точность оценок стабилизируется и в дальнейшем изменяется слабо. Аналогичная особенность отмечается и в статистике амплитуд.
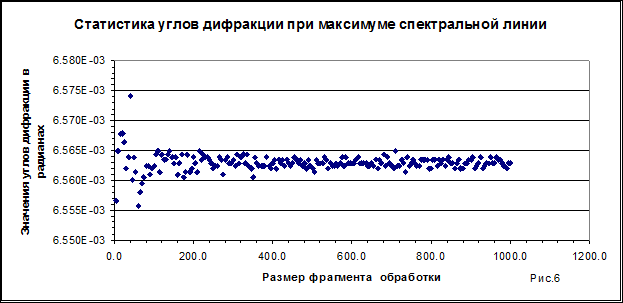
Таким образом, энергия фрагмента обработки определяется в основном шириной спектральной линии. Боковые лепестки спектральной линии вносят в энергию незначительный вклад.
Метод максимального правдоподобия позволяет оценивать положение не только фрагмента принятого сообщения, связанного с максимумом спектральной линии. В этом случае энергия фрагмента принятого сообщения максимальна, и максимум корреляционной функции позволяет оценить амплитуду и положение линии спектра. Однако если необходимо определить положение произвольного фрагмента на принятом сообщении, то его энергия необязательно будет максимальна и использовать корреляционную функция в принципе нельзя. В этом случае минимум функционала правдоподобия (9) дает возможность найти положение фрагмента на оси углов дифракции. В качестве примера будем считать фрагментом интервал от максимума спектральной линии (![]() ) до первого дополнительного максимума, с целью оценки положения первого дополнительного минимума (
) до первого дополнительного максимума, с целью оценки положения первого дополнительного минимума (![]() ).
).
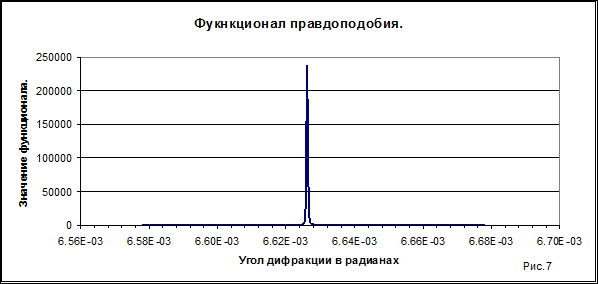 Корреляционная функция в этом случае не дает возможности оценки местоположения первого минимума. В то же время функционал правдоподобия (9) позволяет решить эту задачу. На рис. 7 показана зависимость обратного функционала правдоподобия от угла дифракции.
Корреляционная функция в этом случае не дает возможности оценки местоположения первого минимума. В то же время функционал правдоподобия (9) позволяет решить эту задачу. На рис. 7 показана зависимость обратного функционала правдоподобия от угла дифракции.
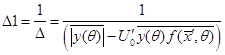 14
14
Максимум на рисунке отображается лучше, чем минимум. Положение максимума функционала определяет значение ![]() радиан. Оно соответствует значению
радиан. Оно соответствует значению ![]() радиан. Таким образом, используя корреляционный фильтр для нахождения произвольного фрагмента принятого сообщения, предпочтителен функционал правдоподобия, а не корреляционная функция.
радиан. Таким образом, используя корреляционный фильтр для нахождения произвольного фрагмента принятого сообщения, предпочтителен функционал правдоподобия, а не корреляционная функция.
Заключение
В настоящей работе рассмотрена возможность применения положений теории оптимального приема к обработке видеоизображений спектроватомов, полученных с помощью дифракционной решетки. Основными являются следующие выводы. Обработка спектральных линий, получаемых с помощью дифракционной решетки, с целью оценки параметров, может проводиться методом максимального правдоподобия. Данный метод позволяет определить оптимальный алгоритм обработки и оценочное значение дисперсии параметров сигнала (дисперсию Рао – Крамера). Точность оценки параметров сигнала, в связи с интегральной обработкой, существенно превышает точность оценки параметров в одной точке (в максимуме спектральной линии). Установлено, что обработка спектральной линии методом максимального правдоподобия может быть проведена по выделенному фрагменту принятого сообщения, определяемого шириной спектральной линии. Энергия этого фрагмента незначительно отличается от полной энергии спектральной линии. Установлено, что максимум функционала правдоподобия точнее определяет положение выделенного фрагмента в принятом сообщении, чем максимум функции корреляции.
Рецензенты:
Захаров В.Е., д.ф.-м.н., профессор, заведующий кафедрой радиофизики и информационной безопасности Балтийского федерального университета им. И. Канта Минобрнауки, г.Калининград.
Волхонская Е.В., д.т.н., профессор, заведующий кафедрой ТОР ФГБОУ ВПО БГАРФ КГТУ, г.Калининград.
Библиографическая ссылка
Бабинович А.И., Пахотин В.А., Либерман И.В. ТЕОРИЯ ОПТИМАЛЬНОГО ПРИЕМА В ПРИЛОЖЕНИИ К АТОМНОЙ СПЕКТРОСКОПИИ // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12308 (дата обращения: 13.02.2026).



