Введение
Изображения, полученные при дистанционном зондировании поверхности Земли, формируются на борту летательного или космического аппарата, где расположены датчики и устройства первичной обработки сигналов. После сформированные данные передаются на наземный пункт обработки, где и происходит их конечная обработка. При неустойчивом канале связи возникает биполярный импульсный шум. Пример изображения, искаженного данной помехой, приведен на рисунке 1. Присутствие таких помех крайне затрудняет анализ изображений, а также ставит под вопросом дальнейшее использование изображения как источника информации. Поэтому важно устранить все импульсные помехи, с наименьшими потерями качества [5, 2].

Рисунок 1 – Изображение, искаженное импульсным биполярным шумом
Будем считать, что изображение является двумерной матрицей размерностью MxN. А яркость каждой точки будет лежать в диапазоне [0,255]. Тогда
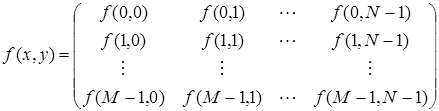 (1)
(1)
Из вышесказанного следует, что если значение в точке ![]() , то это соответствует черному шуму, а
, то это соответствует черному шуму, а ![]() – белому. Тогда импульсную помеху можно описать в виде выражения:
– белому. Тогда импульсную помеху можно описать в виде выражения:
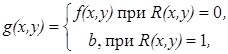 , (2)
, (2)
где ![]() описывает область локализации помехи,
описывает область локализации помехи, ![]() – значение помехи в данной локализации, принимающее только два значения 0 или 255.
– значение помехи в данной локализации, принимающее только два значения 0 или 255.
На основе анализа литературы можно выделить два подхода к фильтрации импульсных помех [1]:
- алгоритмы фильтрации, построенные на основе пространственной фильтрации;
- алгоритмы фильтрации, построенные на основе частотной фильтрации (с использованием Вельвет преобразования).
Первая группа алгоритмов наиболее подробно изложена в литературе [1]. Данные алгоритмы основаны на применении операций, предполагающих преобразование пикселей окрестности изображения с использованием некоторой специальной матрицы. Ту матрицу называют фильтром, ядром, максой, шаблоном и т.д. Значения элементов матрицы принято называть коэффициентами. Как уже отмечалось в [2], наиболее эффективным методом при устранении данного шума является применение к изображению с помехой медианного фильтра размерностью 3x3 (рисунок 2):
![]() , (3)
, (3)
где ![]() – обработанное изображение,
– обработанное изображение, ![]() – маска фильтра размерностью 3х3 пикселя.
– маска фильтра размерностью 3х3 пикселя.
а)  б)
б) 
Рисунок 2 – Применение медианного фильтра. а) исходное изображение, б) отфильтрованное изображение (СКО=8,08)
В данной статье рассматривается методычастотной фильтрации, основанные на преобразовании Уолша. Метод квазидвумерной фильтрации основан на применении преобразования Уолша к строкам или столбцам изображения. Дискретное квазидвумерноепреобразование Уолша имеет вид [3, 5]:
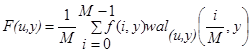 , (4)
, (4)
где ![]() – спектральное представление изображения.
– спектральное представление изображения.
Квазидвумерный спектр изображения представлен на рисунке 3. Применим теорему об ограничении нетригонометрического спектра:
![]() , (5)
, (5)
где ![]() ,
, ![]() ,
, ![]() .
.
и дискретное обратное преобразование Уолша
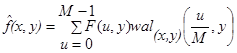 , (6)
, (6)
где ![]() – «усечённое» изображение (рисунок 4).
– «усечённое» изображение (рисунок 4).
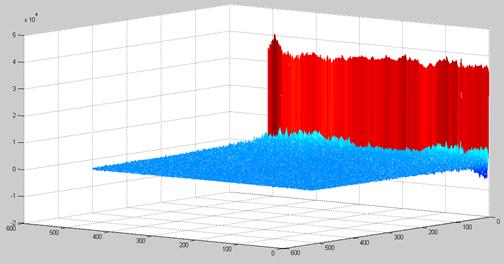
Рисунок 3 – Квазидвумерный спектр изображения

Рисунок 4 – «Усеченое» изоражение
Если применить формулу медианной фильтрации к полученному изображению:
![]() (7)
(7)
и вычесть полученное изображение из изображения с импульсными помехами:
![]() (8)
(8)
где ![]() – матрица изображения,
– матрица изображения, ![]() – матрица нового изображения, M – маска импульсных помех.
– матрица нового изображения, M – маска импульсных помех.
Далее алгоритм можно идти 2мя путями:
- используя значения данной маски применить формулу
![]() (9)
(9)
гдеb – изображение без помех
- зная координаты помех, рассчитать среднюю яркость в выбитом пикселе:
![]() (10)
(10)
Метод двумерной фильтрации основан на применении преобразования Уолша и к строкам и к столбцам изображения:
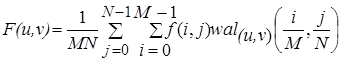 (11)
(11)
Применив теорему об ограничении нетригонометрического спектра:
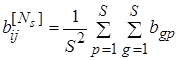 , (12)
, (12)
где ![]() ,
, ![]() ,
, ![]() .
.
и дискретное обратное преобразование Уолша
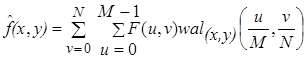 , (6)
, (6)
Далее алгоритм работает по уже описанным шагам.
При сравнении похожих изображений первым встает вопрос: что считать мерой схожести изображений? Очевидно, что это величина имеет значение обратное различию изображений друг от друга. Следственно, нужно выбрать некую метрику, характеризующую различие изображений друг от друга. Тогда схожими изображениями будут считаться изображения, отличие между которыми меньше некоторого порога. В настоящее время наиболее популярными и распространенными метриками, используемыми для оценки качества восстановленных изображений, является среднеквадратическая ошибка (СКО). СКО можно вычислить по формуле [4]:
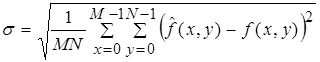 .
.
Анализ данных, приведенный в таблице 1, показывает, что предложенный алгоритм восстанавливает изображение на порядок лучше.
Таблица 1 – Сравнительные характеристики
|
% выбитых пикселей от изображения |
СКО (простр) |
СКО (двум.) |
СКО (квазидв.) |
|
0.01 |
8,29 |
2,11 |
1,58 |
|
0.02 |
8,32 |
2,89 |
2,36 |
|
0.04 |
8,44 |
4,12 |
3,32 |
|
0.005 |
8,25 |
1,48 |
1,02 |
Рецензенты:
Ручкин В.Н., д.т.н., профессор, профессор кафедры Информатика и вычислительная техника,
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Рязанский государственный университет имени С.А. Есенина», г. Рязань.
Овечкин Г.В., д.т.н., профессор, профессор кафедры «Вычислительная и прикладная математика», Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Рязанский государственный радиотехнический университет», г. Рязань.
Библиографическая ссылка
Упакова А.Г. ФИЛЬТРАЦИЯ ИЗОБРАЖЕНИЙ С ИМПУЛЬСНЫМИ ПОМЕХАМИ НА ОСНОВЕ ТЕОРИИ ДИСКРЕТНЫХ СИГНАЛОВ НА КОНЕЧНЫХ ИНТЕРВАЛАХ // Современные проблемы науки и образования. 2014. № 2. ;URL: https://science-education.ru/ru/article/view?id=12304 (дата обращения: 13.02.2026).



