В концепции ФГОС среднего образования одной из ключевых установок является формирование и развитие универсальных учебных действий (УУД). Современная педагогика под универсальными учебными действиями понимает совокупность обобщенных действий учащегося, а также связанных с ними умений и навыков учебной работы, обеспечивающих способность субъектов к самостоятельному усвоению новых знаний, умений и компетентностей, к сознательному и активному присвоению нового социального опыта, к саморазвитию и самосовершенствованию [7]. В [5] поясняется, что в широком значении термин «универсальные учебные действия» означает умение учиться, т. е. способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта.
В более узком (собственно психологическом значении) этот термин можно определить как совокупность способов действия учащегося (а также связанных с ними навыков учебной работы), обеспечивающих его способность к самостоятельному усвоению новых знаний и умений, включая организацию этого процесса [5, с. 27]. Кроме того, в [5] предложены типовые задачи, направленные на формирование УУД, и описаны возможные подходы к диагностике личностных, познавательных, регулятивных и коммуникативных УУД. Однако для основной школы в пособии [8] определены лишь возможные пути формирования и развития УУД, представлены образцы заданий, но подходы к диагностике УУД даже не обозначены. Таким образом, возникает проблема, связанная с недостаточным уровнем разработанности диагностического аппарата, позволяющего определить у учащегося основной школы уровень сформированности УУД.
Естественно, что вопросы формирования УУД, в том числе при изучении учащимися школьного курса геометрии, стали активно обсуждаться в методической литературе (см., например, [1]). Однако и там диагностический инструментарий в лучшем случае описывается в качественных категориях. Это обусловлено, на наш взгляд, описанием подходов к построению методики – обычно просто декларируется возможность формирования УУД какой-либо группы при том или ином варианте изложения темы без указания конкретных УУД и тем более механизмов их формирования. Как следствие, выстроить в такой ситуации диагностический аппарат весьма затруднительно. В работах [3] и [4] нами предложен подход к построению методики с встроенным механизмом формирования УУД познавательного, регулятивного и коммуникативного блоков. Он проиллюстрирован методической разработкой одной из тем геометрии. В данной статье мы намерены обсудить подходы к построению диагностики уровня сформированности УУД указанных трех блоков.
В качестве диагностического инструментария для определения уровня сформированности УУД у учащихся на уроках математики мы предлагаем использовать технологию обучающих тестов, разработанную Н.А. Сеногноевой [6]. Данная технология широко апробирована, прежде всего, в преподавании математических дисциплин. К примеру, Е.В. Вязовова [2] использует ее в целях формирования когнитивной компетентности учащихся. Для нас же важен значительный диагностический потенциал обучающих тестов. На наш взгляд, данная технология позволяет диагностировать уровень сформированности ряда УУД, в первую очередь познавательных и регулятивных, и до некоторой степени УУД коммуникативного блока.
Суть технологии обучающих тестов состоит в том, что в отличие от обычного теста, где учащемуся предлагают выбрать ответ или просто записать то, что у него получилось (после чего учитель может только строить гипотезы, почему у учащегося получился такой ответ), в обучающих тестах учащемуся на каждом шаге предлагается выбрать одно действие из нескольких предлагаемых альтернатив. Каждый раз действие оценивается как продуктивное, т.е. ведущее в нужную сторону (к решению поставленной задачи), или тупиковое. В итоге из этих шагов складывается решение, т. е. явным результатом для учащегося всегда является решенная задача. Отметим, что психологически это немаловажно, поскольку учащийся в результате своей деятельности приходит к решению поставленной задачи. Принципиальной характеристикой обучающего теста является наличие разных путей решения одной и той же задачи. Количество таких путей в диссертации Н.А. Сеногноевой названо шириной теста, хотя более адекватно, на наш взгляд, было бы назвать вариативностью. Эти пути могут быть разной длины в зависимости от выбора теоретического знания, которое ученик будет использовать для решения задачи, от степени свернутости его знаний и умений и т.д. Важно, что выбор учеником действия на том или ином шаге выполнения обучающего теста является проекцией соответствующего УУД, и, значит, прослеживая выбранную учащимся траекторию решения задачи, можно диагностировать, какие УУД уже освоены учащимся, а какие нет. Мы можем зафиксировать, насколько хорошо учащийся умеет отбирать информацию и отделять в ней существенное от несущественного, преобразовывать в знаково-символическую форму и оперировать с ней в таком виде, в какой мере его мыслительные действия свернуты или, наоборот, требуют пошаговой развернутости и т. д.
Чтобы продемонстрировать данный подход, приведем конкретный пример использования технологии обучающих тестов на уроке геометрии для диагностики сформированности УУД.
Учащимся предлагается с помощью обучающего теста решить задачу по теме «Сумма углов треугольника». Занятие проводится с использованием компьютера, поэтому тестовые задания, варианты ответа и диагностика сделанного учеником выбора осуществляются интерактивно. В данном тексте для описания порядка предъявления заданий со всеми альтернативами и диагностиками мы пользуемся следующими приёмами. Учащемуся последовательно предъявляются пункты с заданиями (они пронумерованы числами от 1 до 14 – таково общее количество заданий в данном тесте), ответы к каждому заданию маркированы буквами русского алфавита. После выбора ответа учащемуся предъявляется диагностика и указание по дальнейшим действиям (диагностика ответа маркируется сочетанием буквы Д и порядкового номера).
Ниже приведен начальный фрагмент данного теста с соответствующими комментариями.
Задача. Найдите углы равнобедренного треугольника, если один из них равен 100°.
Инструкция. Для решения задачи выполните пункты в заданной последовательности, начиная с п.1 и выбирая в каждом из них один из предлагаемых в нем ответов.
1. Для решения задачи Вам будет полезна следующая информация:
|
А. Определение равнобедренного треугольника. |
→ |
Переходите к Д1 |
|
Б. Свойство углов при основании равнобедренного треугольника. |
→ |
Переходите к Д2 |
|
В. Свойство высоты, медианы и биссектрисы равнобедренного треугольника, проведенных к основанию. |
→ |
Переходите к Д3 |
|
Г. Другая информация. |
→ |
Переходите к Д4 |
Д1. Вспомните определение и подумайте, поможет ли Вам его знание сразу определить хотя бы один из двух неизвестных углов треугольника, вернитесь к п.1.
Д2. Такой путь возможен, переходите к п.2.
Д3. Такой путь возможен, переходите к п.10.
Д4. Запишите свой вариант в тетради и обсудите с учителем, к какому действию переходить дальше.
Диагностический комментарий. Если учащийся выбирает в качестве ответа пункт А, то это свидетельствует о том, что он ориентируется в данной задаче только на внешний признак – то, что в условии фигурирует равнобедренный треугольник, а не на узловой элемент, состоящий в необходимости информации об углах равнобедренного треугольника. Здесь диагностируется недостаточная сформированность такого УУД, как умение выделить и сформулировать существенную информацию для решения данной задачи.
Если учащийся в качестве ответа выбирает пункт Б, то весьма велика вероятность, что он уже имеет осознанный план решения задачи, что соответствует УУД составление плана и последовательности действий. Это уточнится при прохождении им пункта 2. Но даже в том случае, если окончательного плана решения задачи у него нет, выбор этого пункта свидетельствует о позитивном процессе формирования у него таких УУД, как поиск и выделение необходимой информации; определение основной и второстепенной информации; анализ объектов с целью выделения признаков; выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
Если учащийся выбирает в качестве ответа пункт В, то, хотя такой выбор может привести к решению задачи, весьма вероятно, что этот выбор был сделан почти наугад и узловой момент – информации об углах равнобедренного треугольника – и в этом случае остался вне осознания учащимся. Поэтому и здесь диагностируется недостаточная сформированность такого УУД, как умение выделить и сформулировать существенную информацию для решения данной задачи. Путь, который, в конце концов, приведет ученика к решению, будет длинным, нерациональным и фактически будет случайным блужданием, а самое главное, он свидетельствует о низком уровне сформированности логических УУД. Необходимо по окончанию прохождения учащимся теста предложить ему пройти тест еще раз, выбирая иной путь решения задачи и обсудить, какой из путей предпочтительней и почему.
Если учащийся выбирает в качестве ответа пункт Г, то надо иметь в виду следующее. Вероятнее всего, это тупиковый путь, не ведущий к решению. В этом случае диагностика по существу совпадает с Д1, разумеется, с адаптированным комментарием, почему этот выбор неудачен. Но возможно, что будет высказан вполне приемлемый вариант, например, что нужно воспользоваться теоремой о сумме углов треугольника. Она действительно будет востребована, но позже – в п.4. Поэтому реакция учителя должна быть одобрительной, но он должен обратить внимание ученика, что эта теорема никак не учитывает специфичность треугольника – его равнобедренность, – а значит, вряд ли должна быть первым действием в решении этой задачи. С точки зрения диагностики УУД это означает, что ученик правильно выделяет существенную информацию (речь должна идти об углах), но не умеет планировать последовательность действий, которая будет приводить к решению задачи.
Однако выбор пункта Г положительно диагностирует ряд других УУД. Учащийся прекрасно понимает, что среди пунктов А – В имеется тот, который ведет к решению задачи. Поэтому, выбирая пункт Г, он, во-первых, демонстрирует стремление к самостоятельному выстраиванию траектории своей деятельности (регулятивное УУД), во-вторых, готовность к коммуникации с учителем в творческом процессе (коммуникативное УУД). Разумеется, если ученик выбрал пункт Б или В, это вовсе не означает слабую развитость у него указанных регулятивных и коммуникативных УУД.
2. Свойство углов при основании равнобедренного треугольника говорит о том, что:
|
А. Углы при основании равнобедренного треугольника равны. |
→ |
Переходите к Д5 |
|
Б. Сумма углов при основании равна величине внешнего угла при третьей вершине. |
→ |
Переходите к Д6 |
|
В. Углы при основании равнобедренного треугольника равны 45°. |
→ |
Переходите к Д7 |
|
Г. Углы при основании равнобедренного треугольника равны 90°. |
→ |
Переходите к Д7 |
|
Д. Иная формулировка для этого свойства. |
→ |
Переходите к Д8 |
Д5. Это верно, переходите к п. 3.
Д6. Подумайте, отражает ли это свойство специфику равнобедренности треугольника, вернитесь к п. 2.
Д7. Это неверная формулировка, вернитесь к п. 2.
Д8. Запишите свой вариант в тетради и обсудите с учителем, к какому действию переходить дальше.
Диагностический комментарий. Данный пункт в первую очередь диагностирует знания ученика. Тем не менее, он способствует уточнению диагностик УУД, полученных по результатам выполнения пункта 1. Действительно, если учащийся выбирает в качестве ответа пункт А, то это повышает правдоподобие гипотезы, что он уже имеет план решения задачи в целом. Если же он выбирает какой-то из пунктов Б – Г, то это означает, что такого плана у него нет, а удачный выбор пункта сделан либо случайно либо всё-таки с ориентацией на существенные связи в условии задаче (что уже позитивно, но должно быть подтверждено последующим прохождением теста). Если же он выбрал пункт Д, то либо он дает формулировку, эквивалентную пункту А, но этого не понимает, что свидетельствует о проблемах в логическом мышлении, либо формулировка по сути эквивалентна пунктам Б – Г с соответствующей диагностикой.
3. В равнобедренном треугольнике угол, равный 100°, может быть:
|
А. Одним из углов при основании. |
→ |
Переходите к Д9 |
|
Б. Углом при вершине, противоположной основанию. |
→ |
Переходите к Д10 |
Д9. Вспомните, сколько тупых углов может иметь треугольник, сопоставьте эту информацию со свойством углов при основании равнобедренного треугольника, вернитесь к п.3.
Д10. Это верно, переходите к п.4.
Диагностический комментарий. Здесь не предусмотрен вариант обращения к учителю, поскольку ученику предъявляются две исчерпывающие альтернативы. Как и в п.2, выбор правильной альтернативы повышает правдоподобность гипотезы о наличии у ученика полного плана пути решения задачи; выбор неверной альтернативы свидетельствует о недостаточных знаниях учащегося. Что касается непосредственно УУД, то здесь диагностируется такое УУД, как «подведение под понятия, выделение следствий».
4. Для нахождения неизвестных углов Вы будете:
|
А. Строить равнобедренный треугольник с углом 100° при вершине. |
→ |
Переходите к Д11 |
|
Б. Применять теорему о сумме углов треугольника. |
→ |
Переходите к Д12 |
|
В. Применять свойство высоты, медианы и биссектрисы равнобедренного треугольника, проведенных к основанию. |
→ |
Переходите к Д13 |
|
Г. Использовать другой способ для нахождения углов. |
→ |
Переходите к Д14 |
Д11. Такой путь возможен, переходите к п.5
Д12. Такой путь возможен, переходите к п.7
Д13. Такой путь возможен, переходите к п.10
Д14. Запишите свой вариант в тетради и обсудите с учителем, к какому действию переходить дальше.
Диагностический комментарий. Все действия, предлагаемые в А – В, ведут к решению задачи. Поэтому здесь диагностируются такие УУД, как «выбор наиболее эффективных способов решения задач в зависимости от конкретных условий»; «поиск и выделение необходимой информации». Для варианта Д14 комментарий тот же, что и для Д4.
Пункт 4, как и пункт 1, – это одна из точек разветвления в прохождении данного теста обучаемым. С точки зрения оценки сформированности уровня развития УУД, а также рефлексии учащимся собственных регулятивных и познавательных достижений подобные точки прохождения теста имеют принципиальное значение.
Мы не приводим описание дальнейшего развертывания данного теста, поскольку, как нам кажется, уже в том, что представлено, достаточно отчетливо виден потенциал использования обучающих тестов в качестве диагностического инструментария для определения уровня сформированности УУД. Отметим лишь, что в отличие от тестов, описанных в [6], нами добавлен пункт коммуникации с учителем. Полная структура данного обучающего теста, позволяющая интегративно оценить его потенциал с точки зрения диагностических возможностей, представлена на рисунке 1.
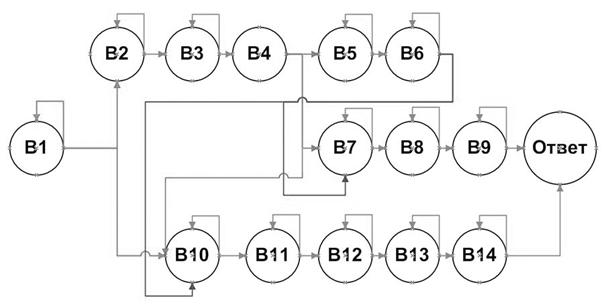
Рис.1. Структура обучающего теста по теме «Сумма углов треугольника»
Как можно увидеть из представленного графа, существует пять различных траекторий прохождения данного теста. Большинство вопросов теста (за исключение вопроса 4) предполагают возвращение к исходному вопросу, если учащийся выбирает тупиковый вариант решения задачи. Таким образом, прохождение всего обучающего теста дает возможность диагностировать уровень сформированности УУД учащегося, который определяется на основании конкретно выбранной им траектории прохождения теста. Важным параметром является и количество «возвратов», допущенных учащимся при прохождении теста.
Рецензенты:
Гейн А.Г., д.п.н., профессор Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Липатникова И.Г., д.п.н., профессор, зав. кафедрой теории и методики обучения математике Уральского государственного педагогического университета, г. Екатеринбург.
Библиографическая ссылка
Журавлев И.А. ДИАГНОСТИКА СФОРМИРОВАННОСТИ УНИВЕРСАЛЬНЫХ УЧЕБНЫХ ДЕЙСТВИЙ У УЧАЩИХСЯ НА УРОКАХ МАТЕМАТИКИ // Современные проблемы науки и образования. 2014. № 1. ;URL: https://science-education.ru/ru/article/view?id=12253 (дата обращения: 11.02.2026).



