На основании экспериментальных исследований [4; 6] установлено, что при сдвиге монолитных шпоночных соединений сборных железобетонных элементов силами 
возникают силы распора в направлении, перпендикулярном оси стыка. В.И. Лишаком предложен метод оценки величины распора, который основан на допущении о проскальзывании контакта между сборным и монолитным бетонами в месте передачи сдвигающего усилия – то есть по опорной площадке. Исходя из этой предпосылки получена формула для определения распора 
:
, (1)
где 
– коэффициент трения сборного бетона о монолитный;
– угол наклона опорной грани шпонки к поперечному сечению стыка;
– коэффициент распора.
Приведенная формула заложена в нормы проектирования [1; 5].
В формуле (1) 
принимается, по разным данным [6; 8; 9], от 0,5 (φ=26,6°) до 0,8 (φ=38,5°). Очевидно, что формула (1) имеет смысл только при 
>φ (то есть допускается проскальзывание по опорной площадке), однако нормы рекомендуют проектировать шпонки с 
во избежание разрушения от проскальзывания. Налицо противоречие.
Экспериментальные данные [6] показывают, что при сдвиге шпоночных стыков с возникает усилие распора, при этом 
в зависимости от геометрических размеров шпонки. На основании этого в нормах [1; 5] установлена минимальная величина 
. В практике проектирования с учетом приведенного выше противоречия во всех случаях используют значение коэффициента
.
Настоящая статья посвящена методике определения величины распора (коэффициента ) без учета проскальзывания бетонной шпонки по опорной площадке (<φ).
Авторами статьи были проведены натурные испытания монолитных шпоночных стыков крупнопанельных зданий [3]. В процессе которых, помимо несущей способности и податливости стыков, определяли усилия распора, возникающие при сдвиге. Для анализа напряженно-деформированного состояния стыков были проведены их численные расчеты. Моделирование шпоночных стыков выполняли объемными конечными элементами и конечными элементами, имитирующими податливые связи на контакте между сборным и монолитным бетонами. Моделирование выполнялось в программной среде ПК «Лира». Жесткости объемных КЭ назначались исходя из класса бетона, податливых связей – по методике, предложенной [7], с учетом образования и развития трещин по контакту.
Усилие распора в численных моделях определялось как отношения растягивающих усилий, возникающих в затяжках, нормальных стыку, и сил сдвига, приложенных ко шву. Результаты определения распорных усилий экспериментальным путем подтвердили результаты численного анализа. Таким образом, установлено, что для определения усилия распора в принципе можно использовать численные модели шпоночных стыков, смоделированные объемными и контактными конечными элементами.
Учитывая, что вертикальный шпоночный стык работает в стесненных условиях и испытывает воздействие сдвиговых продольных сил, приложенных к шпонкам, принято допущение, что его работа аналогична работе стержня на упругом (винклеровском) основании. Рассматриваемый стержень имеет ступенчатое поперечное сечение и работает на восприятие распределённых по длине шпонки моментов и продольных сил, приложенных в местах перемены сечения. Упругое основание представляет собой деформируемый контактный слой на границе монолитного шва и сборного бетона. С учетом принятого допущения усилиями распора в стыке будут суммарные реакции упругого основания. Зная параметры стержня (геометрические характеристики шва, свойства материалов), а также параметры упругого основания (коэффициент постели), можно вычислить величину реакции упругого основания, а следовательно, и величину распора. При этом, конечно, моделирование стыка, как стержня на упругом основании, не позволит адекватно оценить его напряженно-деформированное состояние. Это связано с тем, что указанная модель не учитывает концентрации напряжений на участках, смежных с опорными площадками, и, помимо этого, неравномерной передачи сдвигающих сил со стеновой панели на стык. В связи с вышесказанным предлагаемая балочная аналогия - лишь для вычисления усилий распора.
Для моделирования упругого основания принята модель несвязного упругого основания двустороннего действия Фусса-Винклера [2].
Параметр затухания определяется по формуле:
, (2)
где 
– коэффициент жесткости упругого основания;
– изгибная жесткость шва в соответствующем сечении.
Естественно, параметр затухания будет зависеть от положения сечения. Расчетная схема двухшпоночного стыка представлена на рисунке 1.
Рис. 1. Расчетная схема стыка как стержня на упругом основании
Начиная с некоторого шага шпонок
двухшпоночный стык можно рассматривать как полубесконечный стержень.
Для полубесконечного стержня распределение поперечной силы при действии распределенного момента на расстоянии 
от ее края представлено на рисунке 2.
с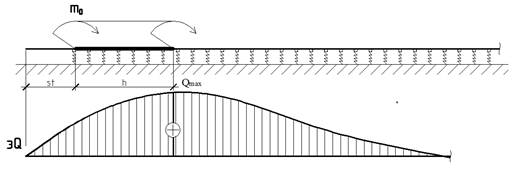
Рис. 2. Распределение поперечной силы 
в полубесконечном стержне на упругом основании от распределенного момента 
Максимальное значение поперечной силы будет равно:
), (3)
Параметры функций 
протабулированы и приведены в справочной литературе, при этом скорость затухания эпюры определяется множителем 
[2].
Величина результирующей реакции упругого основания (фактически усилие распора) есть интеграл реакции по длине от свободного края шпонки до максимального значения поперечной силы. Итак:
, (4)
Величина распределенного момента равна
, (5)
где 
– высота шпонки;
- ширина шва.
С учетом изложенного получено выражение (6) для определения коэффициента 
:
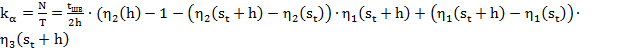, (6)
В работе [2] показано, что при длине свободных концов стержня больше 
его можно считать бесконечным. В связи с этим принято условие, что формулы, применяемые для расчета рассматриваемых полубесконечных стержней, будут справедливы при:
, (7)
В свою очередь, коэффициент с высокой степенью точности можно определить, например, методом конечных элементов, исходя из решения объемной задачи расчета шпоночного соединения, а затем по критерию (7) установить тип стержня (длинный или короткий). Определяя для длинного стержня по формуле (6) и решением объемной задачи, можно достоверно определить 
и коэффициент жесткости основания k из формулы (2).
По предлагаемой методике определены величины для двухшпоночных стыков в зависимости от шага шпонок. График такой зависимости показан на рисунке 3.
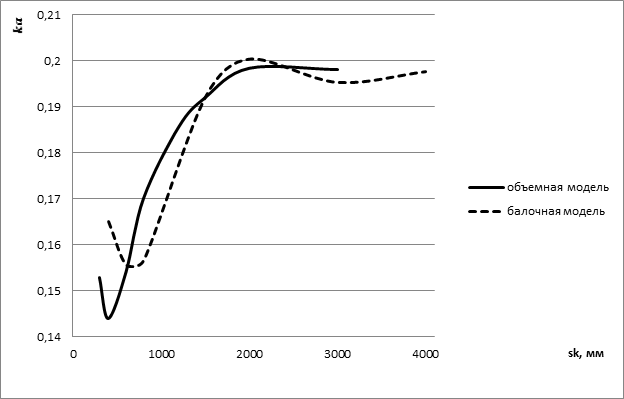
Рис. 3. График зависимости коэффициента для двухшпоночных стыков от шага шпонок 
.
По результатам расчетов МКЭ объемных моделей двухшпоночных стыков заданной конструкции установлено, что длинными стыками можно считать стыки с шагом шпонок
. При данном шаге получено значение 
, откуда по (6) с учетом (2) определен коэффициент жесткости основания 
(в расчетах класс бетона сборного элемента принят равным В22,5).
Расчет стержней с различным шагом шпонок, отвечающим условию
, с использованием полученного выше значения коэффициента жесткости основания
не подтверждает данные, полученные из расчетов объемных моделей.
Распределение реакций упругого основания по границе контакта монолитного и сборного бетонов есть решение контактной задачи. Жесткость контактного слоя в контактных задачах зависит от размеров пятна контакта (в нашем случае от шага шпонок). Таким образом, жесткость податливого основания зависит от шага шпонок.
Коэффициент жесткости основания должен зависеть также и от деформативности материала сборного элемента. На основании сопоставлений значений , полученных в результате расчета численной модели стыка и его балочной модели, выполненных автором, установлено, что указанная зависимость линейна.
При шаге шпонок 
(стержень длинный), величина
– постоянна, ее можно определять, решая уравнение (6) относительно 
при найденном численным моделированием .
Автором предложена формула для определения в зависимости от шага шпонок по длине стыка и характеристик основания:
, (8)
здесь 
;
– эмпирический коэффициент;
– начальный модуль упругости бетона «основания» (сборного элемента).
Используя найденные по формуле (8) коэффициенты жесткости основания, были рассчитаны стержни с различным шагом шпонок. График зависимости коэффициента от шага шпонок, полученный в результате этого расчета, приведен на рисунке 3.
Полученные зависимости от шага шпонок легко аппроксимируются полиномом второй степени при 
. Полученная формула имеет вид:
. (9)
Выводы
1. Величина распора, возникающего при сдвиге шпоночного стыка, определяется в основном реакцией сборных элементов на воздействие момента пары сдвигающих сил.
2. Коэффициент линейной корреляции Пирсона при сопоставлении данных, полученных из расчетов объемной и балочной численных моделей, составил 0,8846, что свидетельствует о возможности моделирования стыков как стержней на упругом основании, при этом следует учитывать зависимость (8).
3. Наиболее простым способом определения коэффициента , при шаге шпонок 
, является метод конечных элементов, поскольку иные методы для расчета стержней на упругом основании весьма трудоемки.
Рецензенты:
Ивашенко Ю.А., д.т.н., профессор, профессор кафедры «Строительные конструкции и инженерные сооружения», ФБГОУ ВПО «Южно-Уральский государственный университет», г. Челябинск.
Потапов А.Н., д.т.н., профессор, заведующий кафедрой «Строительная механика», ФБГОУ ВПО «Южно-Уральский государственный университет», г. Челябинск.
Библиографическая ссылка
Дербенцев И.С., Карякин А.А. МЕТОД ОПРЕДЕЛЕНИЯ УСИЛИЯ РАСПОРА ПРИ СДВИГЕ МОНОЛИТНЫХ ШПОНОЧНЫХ МЕЖПАНЕЛЬНЫХ ВЕРТИКАЛЬНЫХ СТЫКОВ // Современные проблемы науки и образования. – 2014. – № 1. ;URL: https://science-education.ru/ru/article/view?id=12252 (дата обращения: 09.12.2024).