Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Маланин В.В. 1 Остапенко Е.Н. 1 Пенский О.Г. 1

---

1 ФГБОУ ВПО «Пермский государственный национальный исследовательский университет»

Дан краткий обзор возможностей строительных артиллерийских систем, предназначенных для застреливания строительных элементов в грунт. Показано, что существующие одноствольные строительные пушки способны застреливать сваи в грунт на расстояние до 4 м. Предложены математические модели предварительного и второго периодов выстрела многоствольных откатных строительных орудий с разными техническими характеристиками стволов. Получено необходимое условие вертикального застреливания свай из этих орудий при условии равенства сил, воздействующих на застреливаемую сваю. Приведен пример использования необходимого условия для двуствольной строительной артиллерийской системы. Модели, приведенные в статье, могут использоваться при проектировании строительных артиллерийских систем, предназначенных для застреливания свай в грунт на расстояние до 6 м.

Статья в формате PDF

233 KB

основная задача внутренней баллистики

внутренняя баллистика

пушка

свая

строительный элемент

1. Бугаенко Г.А., Маланин В.В., Яковлев В.И. Основы классической механики : учеб. для вузов. – М. : Высшая школа, 1999. – 367с.

2. Маланин В.В., Пенский О.Г. Сопряженные модели динамики импульсно-тепловых машин и проникания недеформируемых тел в сплошную среду : монография. – Пермь : Перм. гос. ун-т, 2007. – 199 с.

3. Маланин В.В., Пенский О.Г., Проничев А.А., Ракко А.Ю. Установка для погружения в грунт строительных элементов : Патент России № 2348757.2009. Бюл. № 7.

4. Пенский О.Г., Проничев А.А. Многоствольная артиллерийская установка для погружения в грунт строительных элементов // Изобретатель. - 2010. - № 10 (130). – Минск. – С. 15 – 19.

5. Пенский О.Г., Остапенко Е.Н., Черников А.В. Уравнения энергетического баланса многоствольных строительных откатных артиллерийских систем // Вестник Пермского университета. Математика. Механика. Информатика. – 2013. - № 1 (13). – Пермь : Перм. гос. ун-т. – С. 34 – 37.

6. Русяк И.Г., Ушаков М.М. Внутрикамерные гетерогенные процессы в ствольных системах : монография. – Екатеринбург : Изд-во УрО РАН, 2001. – 258 с.

7. Цирульников М.Ю., Хабибуллин Р.Х., Шафран С.Б., Гвиндяев Б.Н., Григорьев В.Н., Пенский О.Г. Установка для погружения строительных элементов : авт. св-во СССР 1258105.1986. Бюл. № 9.

8. Pensky O.G. Engineering Construction Cannons: Theory and Practice // Journal of Civil Engineering. – 2013. - Vol. 7, № 17. – P. 1 – 6.

Введение

В настоящее время создана математическая теория, разработаны и внедрены в промышленность одноствольные строительные артиллерийские орудия [8]. Применение на практике строительных пушек показало их большую эффективность в нефтегазовом и промышленном строительстве.

Однако основным недостатком созданных орудий является невозможность их использования для застреливания свай на большие глубины при помощи одного выстрела. Так, например, максимальная величина проникания свай в глинистый грунт с консистенцией 0,5 при использовании установки УЗАС-2, созданной на базе модернизированного крупнокалиберного артиллерийского орудия М-47 [7], составляет 3,8 м [2]. Поэтому перед разработчиками строительных пушек встала задача создания артсистемы, способной застреливать сваи на большую глубину. В работе [3] была предложена принципиальная схема многоствольных откатных пушек. На рис. 1 приведена эта принципиальная схема.

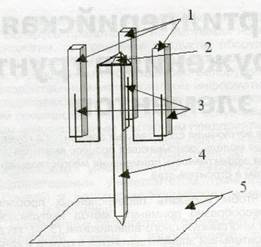
Рис. 1. Принципиальная схема многоствольной строительной артиллерийской системы

Работает установка следующим образом. В стволы 1 вставляется фигурный поршень 3 с платформой 2, которая опирается на строительный элемент 4, упирающийся в поверхность грунта 5. Во время выстрела платформа 2 давит на сваю 4, в результате чего свая 4 проникает в грунт 5.

В работе [4] предложены математические модели, основанные на термодинамической теории выстрела и описывающие внутрибаллистические процессы в стволах 1 при условии, когда все артиллерийские системы, объединенные в единый многоствольный строительный комплекс, обладают одинаковыми техническими характеристиками и имеют одинаковые условия заряжания. Показано, что для трех одинаковых откатных модернизированных орудий М-47 [4], объединенных в единую систему, возможно погружать сваи с помощью одного выстрела в глинистый слой на глубину до 5,3 м.

Математическая формулировка необходимого условия

Пусть в схеме, изображенной на рис. 1, используются орудий. Так как при использовании в промышленности строительных артиллерийских орудий важны требования противопожарной безопасности, то будем предполагать, что во внутрибаллистических процессах выстрела каждого из орудий обязательно присутствует второй период выстрела, который обусловливает отсутствие выброса пламени из стволов при выходе из них строительного элемента. При построении математической модели введем следующие допущения.

1. Стволы артиллерийских орудий опущены вниз под углом 90○ к поверхности грунта, что обеспечивает вертикальное заглубление строительного элемента.

2. Стволы без нарезов, т.е. рассматриваются только гладкоствольные системы, которые обеспечивают движение строительного элемента в грунте без вращения относительно его продольной оси.

3. Для откатных орудий не учитывается работа, затрачиваемая на перемещение газов и заряда. Это можно сделать, приняв во внимание то, что веса зарядов в рассматриваемых случаях чрезвычайно малы по сравнению с весами откатных частей пушек и строительного элемента, и, следовательно, кинетическая энергия заряда в каждой пушке будет настолько мала по сравнению с кинетическими энергиями откатных частей и строительного элемента, что ею можно пренебречь.

4. Давление газов на дно каждого канала ствола многоствольной системы и на строительный элемент от газов в этом стволе одинаково.

5. Состав продуктов горения не меняется, и величина силы пороха f и коволюма пороховых газов α постоянны.

6. Показатель адиабаты θ+1 пороховых газов принимается постоянным, равным некоторому среднему значению.

7. Предполагается, что строительный элемент стоит на месте, пока давление газов не достигает величины давления форсирования , где - номер орудия в многоствольной строительной артиллерийской системе, .

8. Движение строительного элемента по каналу стволов рассматривается до момента прохождения его днища через дульный срез ствола с наименьшим относительным перемещением элемента.

9. Растяжением стенок ствола при выстреле и прорывом газов через зазоры между строительным элементом и каналом ствола пренебрегается.

10. Застреливаемый строительный элемент – недеформируемое тело.

11. Рассматривается выстрел без учета сопротивления грунта движению строительного элемента.

12. Орудия, входящие в многоствольную строительную артиллерийскую систему, имеют разные технические характеристики и условия заряжания.

13. Силы, возникающие при горении пороха в каждом из стволов и давящие на сваю во время выстрела, равны.

Уравнения энергетического баланса для первого периода выстрела приведены в работе [5].

Так как при использовании в промышленности строительных артиллерийских орудий важны требования противопожарной безопасности, то будем предполагать, что во внутрибаллистических процессах выстрела каждого из орудий обязательно присутствует второй период выстрела, который обусловливает отсутствие выброса пламени из стволов при выходе из них строительного элемента.

Запишем уравнения внутренней баллистики каждого из стволов, входящих в многоствольную систему, для второго периода выстрела.

Во втором периоде выстрела пороховые газы расширяются адиабатически, и поэтому справедливы соотношения [6]

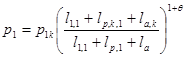, (1)

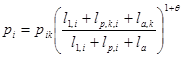, (2)

где - давление в канале ствола с номером , - давление в канале ствола в конце первого периода выстрела, - приведенная длина каморы в конце первого периода выстрела, - путь свободного отката ствола в конце первого периода выстрела, - абсолютный путь выстреливаемого строительного элемента в конце первого периода выстрела, откат ствола во втором периоде выстрела, , - абсолютный путь строительного элемента во втором периоде выстрела.

На основе второго закона Ньютона [1] можно записать уравнения, описывающие динамику пушек и строительного элемента:

, (3)

, , (4)

, (5)

где - время, - масса первого и ствола соответственно, - масса застреливаемого строительного элемента, - ускорение силы тяжести, - площади поперечного сечения первого канала ствола и канала ствола соответственно.

При работе многоствольных артиллерийских систем важно, чтобы во время выстрела не возникали моменты сил, способные развернуть строительный элемент относительно вертикали. При условии, что плечи поршня-забойника, который при выстреле толкает строительный элемент вниз, равны, условие отсутствия моментов можно записать в виде соотношения , которое эквивалентно равенству

. (6)

Подставляя соотношение (6) в формулу (2), учитывая справедливость равенства и проводя несложные преобразования, получим формулу

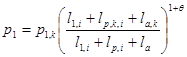. (7)

Приравнивая правые части соотношений (1) и (7), получим равенство

,

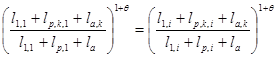которое влечет формулу

, (8)

где

. (9)

Дифференцируя дважды соотношения (8) по параметру и учитывая равенства (3) – (6), после несложных преобразований получим:

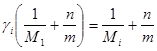. (10)

Выражая из равенства (10) величину , получим:

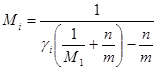, . (11)

Исходя из логики вышеприведенных рассуждений, можно сделать вывод о том, что равенства (11) являются необходимым условием отсутствия моментов вращения во втором периоде выстрела при условии равенства толкающих сваю сил, возникающих за счет давления пороховых газов в каждом стволе, при застреливании сваи в грунт из многоствольного строительного артиллерийского орудия.

Пример использования необходимого условия

В качестве примера использования необходимого условия (11) рассмотрим двуствольную систему (очевидно, что в этом случае справедливо равенство ), состоящую из модернизированного артиллерийского орудия М-47 (установка УЗАС-2) и гарпунно-китобойной пушки ГКП-БМ, снятых с вооружения СССР в конце 1970-х годов.

Технические характеристики модернизированной системы М-47 и системы ГКП-БМ, необходимые для дальнейших расчетов, приведены в табл. 1.

Таблица 1. Технические характеристики

Пусть в процессе застреливания строительного элемента в грунт отсутствует первый период выстрела, и предварительные периоды выстрела для обеих артсистем заканчиваются в одно и то же время.

Легко видеть, что в этом случае справедлива формула , которая согласно теории внутренней баллистики ствольных систем [6] эквивалентна соотношению

,

где - объемы камор первого и второго стволов соответственно, - коволюм пороховых газов, - масса пороха в первом стволе, - масса пороха во втором стволе.

Будем предполагать, что строительный элемент, не разрушаясь, выдерживает при выстреле максимальное давление, равное . Примем это давление в качестве давления форсирования для первого орудия, причем справедливо неравенство .

Согласно [6] первый период выстрела описывается соотношением

,

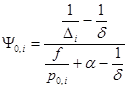где - номер ствола, - относительная часть сгоревшего пороха в предварительном периоде выстрела в стволе , , - плотность пороха, - сила пороха, - давление форсирования в стволе , здесь .

Очевидно, что давления форсирования удовлетворяют соотношению

. (12)

Согласно равенству (12) и нашему предположению об отсутствии первого периода выстрела в обоих стволах справедлива формула , которая влечет соотношения

, (13)

. (14)

Для расчета выстрела с техническими параметрами пушек, приведенными в табл. 1, примем следующие значения для входных внутрибаллистических параметров модели: =250 МПа, 95000 Дж, =0,001 м3/кг, 360 кг, 0,154 кг.

Результаты и схема расчетов, использующих последовательно соотношения (13), (14), (12) и (11), приведены в табл. 2.

Таблица 2. Схема и результаты расчетов

Анализ последних двух строк табл. 2 позволяет сделать вывод о том, что необходимое условие (11) отсутствия вращательных моментов сил при выстреле при не выполняется и, следовательно, применять модернизированную пушку М-47 и пушку ГКП-БМ, объединенные в единую двуствольную строительную артсистему, при заданных условиях заряжания нельзя.

Заключение

Таким образом, в настоящей статье приведено необходимое условие отсутствия вращательного момента сил строительного элемента при выстреле многоствольной строительной артсистемы. Отметим, что, хотя это условие не является достаточным, но, благодаря простоте расчетных формул, оно позволяет без использования методов программирования быстро определять возможности многоствольной строительной артиллерийской системы по застреливанию строительных элементов, исключающей возникновение моментов сил, влекущих поворот элементов относительно вертикального направления застреливания.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (базовая часть государственного задания на проведение научно-исследовательских работ).

Рецензенты:

Тарунин Е.Л., д.ф.-м.н., профессор, профессор кафедры прикладной математики и информатики, Пермский государственный национальный исследовательский университет, г. Пермь.

Ясницкий Л.Н., д.т.н., профессор, заведующий кафедрой прикладной информатики, Пермский государственный гуманитарно-педагогический университет, г. Пермь.

Пачурин Герман Васильевич, д.т.н., профессор, зав. кафедрой «Производственная безопасность и экология» (ПБиЭ), Нижегородский государственный технический университет им. Р.Е. Алексеева, г. Нижний Новгород.

Библиографическая ссылка