Введение
Корректность определения передаточных отношений преобразующего механизма позволяет обеспечить работоспособность привода технологического оборудования посредством согласования входных и выходных параметров энергетической и рабочей машин. Повышение эффективности операций, реализуемых при помощи технологического оборудования, является актуальной задачей, решение которой возможно обеспечить посредством использования механизмов с замкнутой системой тел качения (ЗСТК), обладающих требуемыми передаточными отношениями и позволяющих реализовать сложное движение выходного звена при минимально возможном числе подвижных звеньев. Механизмы с ЗСТК обладают структурой, которая образована совокупностью двух колец с дорожками качения, сепаратора (водило) и тел качения с диаметрами равной или разной величины, которые могут обладать рабочими поверхностями с выступами (зубчатые) [1] или гладкими поверхностями (фрикционные) [2-10].
Коллектив авторов проводит исследования геометрических и кинематических параметров исполнительных механизмов технологического оборудования, разработанного на базе механизмов с ЗСТК с диаметрами разной (эксцентриковые) [1; 2; 6-10] или равной (соосные) [3-6] величины. В ходе исследований установлено: если замкнутая система тел качения обладает диаметрами равной величины, то задача определения номинальных значений геометрических параметров механизмов с ЗСТК должна решаться при начальных условиях, что исходные параметры являются постоянными величинами больше нуля при наличии или отсутствии зазора между телами качения
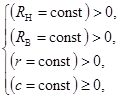(1)
где RВ и RН – радиусы дорожек качения внутреннего и наружного колец; r и c – радиус тел качения и зазор между ними.
Для решения задачи по определению номинальных величин геометрических параметров при системе (1) необходим ввод поправки в расчет, считая, что один из исходных параметров является величиной переменной. Вариация значениями радиуса тел качения и зазора не позволяет достичь требуемого результата. В этом случае получаем, что решение имеет два возможных направления ввода поправки, т.е. либо 
, либо 
.
Настоящее исследование проводится с целью разработки алгоритма определения передаточных отношений механизмов с замкнутой системой тел качения с диаметрами равной величины для любого вида симметричной структурной схемы при ведущем внутреннем кольце посредством ввода поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Полученные результаты позволят формировать приводы технологического оборудования на базе механизмов с ЗСТК, обладающих требуемыми величинами передаточных отношений.
Методы исследования, применяемые в настоящей работе, основаны на принципах кинематического анализа эпициклических механизмов при использовании положений геометрии и метода обращенного движения.
В соответствии с вышеуказанной целью начальные условия системы (1) примут следующий вид
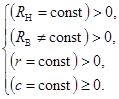(2)
Система (2) позволяет получить два возможных варианта структуры механизма с ЗСТК с диаметрами равной величины, как при наличии, так и при отсутствии зазора между телами качения.
Следуя условию существования [8], число тел качения механизмов с ЗСТК с диаметрами равной величины и зазором найдем по формуле
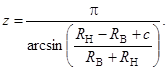(3)
При начальных условиях системы (2) и в соответствии с выбранным направлением ввода поправки в расчет номинальных величин геометрических параметров преобразование равенства (3) позволит получить формулу для вычисления радиуса дорожки качения наружного кольца
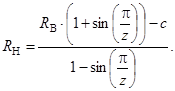(4)
Механизмы с ЗСТК с диаметрами равной величины являются представителями эпициклических механизмов, следовательно, обладают тремя видами передаточного отношения: прямое, обратное и внутреннее, а также являются реверсивными. В зависимости от особенностей структуры, связанных с сочетанием подвижных и неподвижных звеньев, эпициклические механизмы данного вида являются либо планетарными, либо дифференциальными, которые могут работать в режиме редуктора (при 
) или мультипликатора (при 
).
Рассмотрим ход решения поставленной задачи по определению всех видов передаточных отношений на примере планетарного механизма с замкнутой системой тел качения (ЗСТК) с диаметрами равной величины и зазором при ведущем внутреннем кольце, неподвижном наружном кольце и сепараторе (водило) в качестве выходного звена, считая, что движение звеньев совершается без скольжения (проскальзывания). Для этого составим расчетную модель (рис. 1) и примем следующие обозначения: 
, 
и ОВ, OН – дорожки качения и геометрические центры внутреннего и наружного колец; S – сепаратор (водило); 
, 
, 
и 
, 
, 
– радиусы и углы положения тел качения; c – зазор между телами качения.
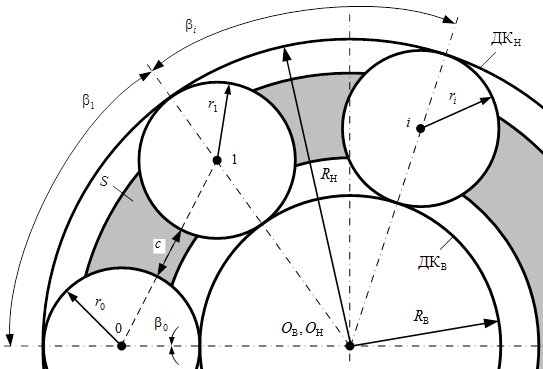
Рис. 1. Расчетная модель механизма с ЗСТК с диаметрами равной величины и зазором
Формулу для прямого передаточного отношения планетарного механизма с ЗСТК с диаметрами равной величины и зазором при ведущем внутреннем кольце, неподвижном наружном кольце и сепараторе (водило) в качестве выходного звена получим, используя метод обращенного движения
(5)
где 
– внутреннее передаточное отношение механизма рассматриваемого вида при ведущем внутреннем кольце и неподвижном сепараторе (водило).
Внутреннее передаточное отношение механизма с ЗСТК с диаметрами равной величины и зазором
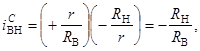(6)
здесь знаки «+» и «–» соответствуют внутреннему и внешнему контактам дорожек качения наружного и внутреннего колец с телами качения.
Подставив (4) в (6) и преобразовав, будем иметь
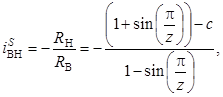(7)
С учетом (7) приведем формулу (5) к окончательному виду
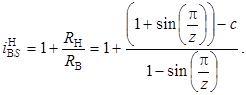(8)
Формула (8) позволяет определить прямое передаточное отношение планетарных механизмов с ЗСТК с диаметрами равной величины и зазором при ведущем внутреннем кольце, неподвижном наружном кольце и сепараторе (водило) в качестве выходного звена для обоих направлений ввода поправки в расчет геометрических параметров.
Обратное передаточное отношение планетарных механизмов с ЗСТК с диаметрами равной величины имеет место при ведущем сепараторе (водило), неподвижном наружном кольце и внутреннем кольце в качестве выходного звена, тогда с учетом (8) получим
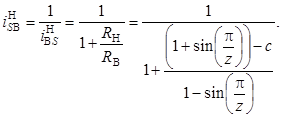(9)
Варьируя числом тел качения в диапазоне (0-100) и значением радиуса дорожки качения внутреннего кольца в интервале (55-100) мм, проведем вычисления по выражениям (7)-(9) для всех видов передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины и зазором 
. Расчет выполняем для начальных условий по системе (2). С целью повышения эффективности процесса реализуемых вычислений авторами разработано программное обеспечение, которое представляет собой программный комплекс «Эксцентрик», зарегистрированный в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности Российской Федерации (РОСПАТЕНТ № 2012614197).
Анализ результатов вычислений показывает, что изменение величины радиуса дорожки качения внутреннего кольца в выбранном интервале не оказывает существенного влияния на диапазоны значений передаточных отношений механизмов рассматриваемого вида. По результатам вычислений выполняем синтез диаграммы передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины и зазором при ведущем внутреннем кольце и вводе поправки по радиусу дорожки качения этого же звена (рис. 2).
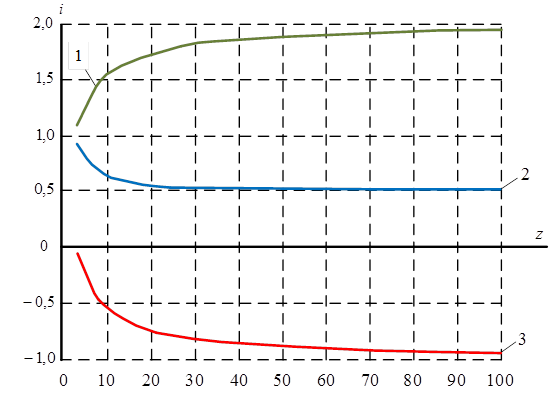
Рис. 2. Диаграмма передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины при ведущем внутреннем кольце и вводе поправки по радиусу дорожки качения этого же звена: 1 – 
; 2 – 
; 3 – 
Анализ диаграммы (рис. 2) показывает, что ввод поправки в расчет по радиусу дорожки качения внутреннего кольца позволяет планетарным механизмам с ЗСТК с диаметрами равной величины обладать передаточными отношениями в диапазонах: прямое 
, обратное 
и внутреннее 
. Это означает, что рассматриваемые механизмы являются редукторами, т.е. силовыми механизмами, так как прямое передаточное отношение 
. Значения обратного передаточного отношения указывают на то, что при ведущем сепараторе (водило), неподвижном наружном кольце и внутреннем кольце в качестве выходного звена планетарные механизмы с ЗСТК при данных условиях находятся в режиме мультипликатора, так как 
, т.е. являются кинематическими механизмами. Ввод поправки по выбранному направлению незначительно расширяет диапазон значений прямого передаточного отношения, т.е. обеспечиваются максимально возможные величины передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины. При этом рост числа тел качения приводит к увеличению только прямого передаточного отношения, так как при данных условиях внутреннее и обратное передаточные отношения уменьшаются.
Разработанный алгоритм определения передаточных отношений механизмов с ЗСТК с диаметрами равной величины применим для любого вида симметричной структурной схемы механизмов рассматриваемого вида при ведущем внутреннем кольце и вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Полученные результаты прошли апробацию на Международной научно-практической конференции (проект Sworld) [1; 7; 8], а также на IV Международной научно-практической дистанционной конференции, посвященной теме «Наука и образование» [10]. Используя результаты исследования, авторами разработано программное обеспечение, которое представляет собой программный комплекс «Эксцентрик», зарегистрированный в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности (РОСПАТЕНТ № 2012614197).
Заключение. В результате проведенных действий выявлены все виды передаточных отношений планетарных механизмов с ЗСТК с диаметрами равной величины при ведущем внутреннем кольце, получены формулы для определения их величин, а также установлены возможные диапазоны их значений и режимы работы формируемых механизмов при вводе поправки в расчет по дорожке качения внутреннего кольца. Это позволяет формировать приводы технологического оборудования на базе планетарных механизмов с ЗСТК, обладающих требуемыми величинами передаточных отношений, а также посредством согласования выходных и входных параметров энергетической и рабочей машин обеспечить работоспособность привода технологического оборудования.
Рецензенты:
Петровский Э.А., д.т.н., профессор, заведующий кафедрой технологических машин и оборудования нефтегазового комплекса, ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.
Желукевич Р.Б., д.т.н., доцент, профессор кафедры авиационных горюче-смазочных материалов, ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.
Мишин В.М., д.т.н., профессор, профессор кафедры «Строительство», Северо-Кавказский федеральный университет, г. Пятигорск.
Библиографическая ссылка
Мерко М.А., Меснянкин М.В., Кайзер Ю.Ф., Колотов А.В., Митяев А.Е., Лысянников А.В., Кузнецов А.В. ПЕРЕДАТОЧНЫЕ ОТНОШЕНИЯ ПЛАНЕТАРНЫХ МЕХАНИЗМОВ С ЗСТК С ДИАМЕТРАМИ РАВНОЙ ВЕЛИЧИНЫ ПРИ ВЕДУЩЕМ ВНУТРЕННЕМ КОЛЬЦЕ И ВВОДЕ ПОПРАВКИ ПО РАДИУСУ ДОРОЖКИ КАЧЕНИЯ ЭТОГО ЖЕ ЗВЕНА // Современные проблемы науки и образования. 2014. № 1. ;URL: https://science-education.ru/ru/article/view?id=12219 (дата обращения: 27.06.2026).