Актуальность исследования. Применение нейронных сетей для решения различных задач стало актуальным в последние несколько лет. Это, в первую очередь, задачи классификации образов, кластеризации/категоризации, аппроксимации функций, предвидения/прогнозирования, формирование памяти с содержательно зависимой адресацией, управления и оптимизации. Так, решая ту или иную задачу нейросети, прежде всего конструируют и в обязательном порядке данную сеть обучают. Обучают приему правильного, точнее адекватного, приема решения. Однако за много лет применения нейронных сетей актуальность их работы заключается в выборе топологии нейросети, алгоритма обучения, активационных функций нейронов и ряда числовых параметров для каждой практической задачи. Обучение сети может осуществляться при помощи различных алгоритмов. Выбор необходимого подхода основывается на критериях скорости и качества обучения.
Генетические алгоритмы обучения являются достаточно мощным средством и могут с успехом применяться для широкого класса прикладных задач, включая те, которые трудно, а иногда и вовсе невозможно решить другими методами. Хотя такие алгоритмы, как и другие методы эволюционных вычислений, не гарантируют выявление глобального решения за определенно короткое время. Генетические алгоритмы не гарантируют и того, что глобальное решение будет найдено, однако они хороши для поиска адекватного решения задачи за довольно короткие сроки. Одним из преимуществ таких алгоритмов является то, что они могут применяться даже на сложных задачах, там, где не существует никаких других, эффективных методов решения. Все же на сегодняшний день вопрос исследования генетических алгоритмов для обучения сетей обратного распространения ошибки остается открытым, что и послужило выбором темы исследования.
Постановка проблемы. Останавливаясь на изучении сетей обратного распространения ошибки, на первый план выходит проблема обучения данных сетей для решения той или иной задачи, поставленной перед пользователем. Научная литература раскрывает массу трудов известных ученых, которые исследуют и применяют различные алгоритмы и методы для обучения нейросетей, говоря о достоинствах и недостатках каждого из них. Однако механизм правильного и точного обучения сетей обратного распространения ошибки не найден. Мало того, большинство предложенных методов мало эффективны и требуют достаточно длительного времени на обучение. Основываясь на этом, возникает вопрос об исследовании генетического алгоритма как основного метода для обучения сетей обратного распространения ошибки.
Анализ исследований и публикаций. В научных трудах по теме исследования освещаются различные аспекты проблематики применения генетического алгоритма для обучения сетей. В то же время заметим, что исследованием проблем обучения нейронных сетей на протяжении многих лет занимались такие отечественные и зарубежные ученые, как Р. Каллан [1], Ф. Уоссермен [2], С. Осовский [3], R. Lopez [4], О.И. Федяев, Ю.И. Соломка [5], С. Короткий [6], И.В. Заенцев [7] и другие. С момента появления известных трудов И.В. Заенцева прошли десятки лет, однако методики составления и обучения нейронных сетей продолжают развиваться достаточно бурно. Хотя на Украине практически отсутствуют исследования, которые могли бы успешно быть реализованы на практике обучения сетей. Требуют дальнейшего усовершенствования и развития методы обучения сетей обратного распространения ошибки.
Отметим, что начало изучению и усовершенствованию нейронных сетей было положено Мак-Каллоком и Питтсом. Они первыми ввели понятие «порогового логического нейрона» и описали логическую модель нейросетей [8]. Вопросом обучения нейронных сетей долгое время занимался российский ученный А.Н. Горбань [9], чему и посвятил свою работу «Обучение нейронных сетей», вышедшую в 1990 году. Этот сборник стал толчком к последующим открытиям.
Цель работы. Обучение сетей обратного распространения ошибки с использованием генетических алгоритмов. Исследование нейронной сети обратного распространения ошибки. Предложение метода применения генетического алгоритма для обучения нейронной сети, составление блок-схемы работы алгоритма, описание процесса обучения, получение положительного результата минимизации ошибки.
Изложение основного материала. Нейронная сеть обратного распространения включает в себя несколько слоев нейронов, при этом каждый нейрон i-го слоя связан с каждым нейроном i+1 слоя.
Рассматривая общий случай обучения нейронных сетей, следует отметить, что этот процесс сводится к нахождению функциональной зависимости у = f(х), где х - входной, а у - выходной векторы. Однако такая задача будет иметь бесконечно огромное множество решений.
Рассмотрим возможность использования генетического алгоритма для обучения сетей обратного распространения ошибки.
Анализируя исследования использования генетических алгоритмов для обучения нейросети, следует отметить, что данные алгоритмы ускоряют работу обучения, однако не являются точными. При потребности более точного решения задачи необходимо разрабатывать комбинированные методы, способные быстро закрыть пробелы сети.
Рассмотрим нейросистему, которая состоит из одного нейрона, заданного функцией активации [10]:
(1)
Структура нейронной сети представлена на рис. 1.
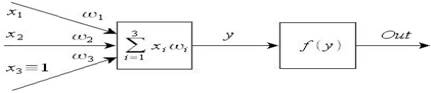
Рис. 1. Структура нейронной сети [10]
При решении задачи необходимо найти такие значения весов ω1, ω2, ω3, для которых при подаче на вход сети сигналов x1 и x2 на ее выходе появлялись бы значение «0» или «1» в соответствии с таблицей истинности для данной логической функции. Исходя из рис. 1 очевидно, что для выбранной функции активации выход нейросети Out приобретает значение «0» или «1» только при 
. Исходя из этого, примем, что обучение проведено успешно, при условии, что выход сети Out больше 0,5 при желаемом выходе T = 1 и меньше 0,5 – при желаемом выходе T = 0 для всех случаев. Функция активации нейросети представлена на рис. 2.
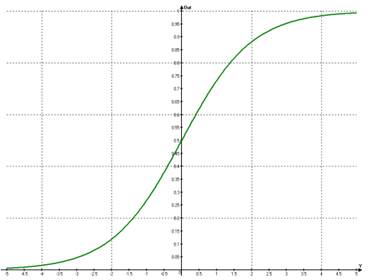
Рис. 2. Функция активации нейросети
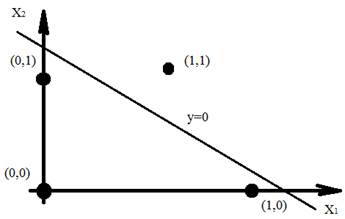
Рис. 3. Разграничение входных векторов обучающих пар на две категории
Точками на рис. 3 показано положение входных векторов обучающих пар. По условию задачи для точки (1,1) значение выхода сети Out должно быть больше 0,5, а для точек (0,0), (0,1) и (1,0) – меньше. При заданной функции активации выход сети Out , равный 0,5, когда
(2)
Таким образом, процесс обучения заключается в таком изменении весов ω1, ω2, ω3, чтобы прямая y=0 разделяла точки на плоскости аналогично, как это показано на рис. 3. Все точки, что выше прямой, будут отвечать желаемому выходу T=1, а все, что ниже – T=0. Тогда значение весов ω1, ω2, ω3 является решением поставленной задачи. Из рисунка видно, что таких прямых можно провести огромное множество. Следовательно, существует множество решений для данной задачи. Однако для того, чтобы определить это множество решений, необходимо воспользоваться следующими утверждениями:
1) для точек, лежащих ниже прямой y = 0, y < 0;
2) для точек, лежащих выше прямой y = 0, y > 0.
Исходя из этого, следует отметить, что если применить описанное утверждение для каждой из четырех точек, показанных на рис. 3, то можно записать следующие неравенства [7]:
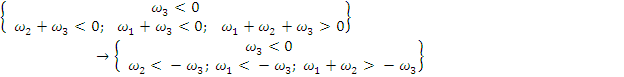
Описанные неравенства приводят область в пространстве весов, внутри которой все точки (ω1, ω2, ω3) являются решениями поставленной задачи.
Поскольку в пространстве труднее графически изобразить точки, чем на плоскости, зафиксируем одну из весов (например, ω3) и перейдем к области решений на плоскости:
На основании этого получим область решений, которая представлена на рис. 4.
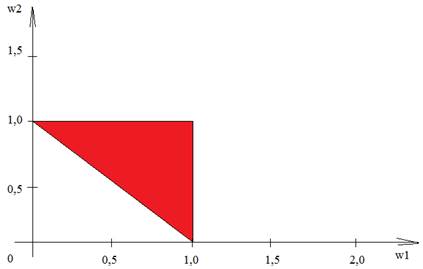
Рис. 4. Область решения задачи 
Таким образом, каждая точка на рис. 4 будет графическим представлением одного из вариантов решения задачи.
Далее применим генетический алгоритм для обучения нейросети. Блок-схема работы алгоритма представлена на рис. 5.
При использовании генетического алгоритма для обучения сетей обратного распространения ошибки каждая особь будет описываться двумя хромосомами: ω1 и ω2.
Теперь для оценки качества полученного решения зададим значение функционала погрешности в виде
(3)
где Out – выход сети, T – желаемое значение выхода. Исходя из условия, следует заметить, что количество обучающих пар равно четырем.
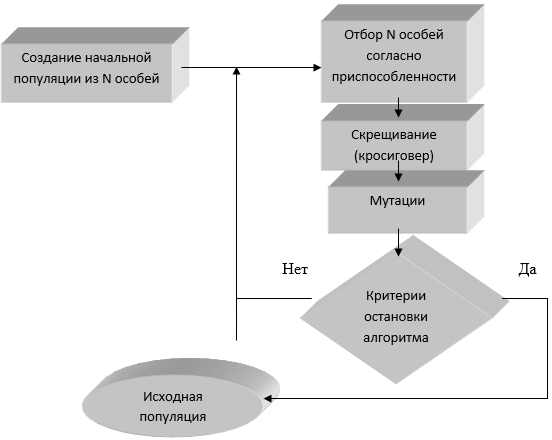
Рис. 5. Блок-схема работы генетического алгоритма
Согласно этому функционал погрешности по всем обучающим парам будет равен [7]
(4)
Основной задачей генетического алгоритма является минимизация погрешности E4.
Основываясь на проведенном исследовании, максимально умным значением функционала погрешности для каждой обучающей пары будет значение Emax=0,125. Тогда E4 max=0,5.
Выводы
Обучение сетей обратного распространения ошибки является достаточно важным этапом в работе с нейросетями для решения задач. Исследовав нейронную сеть обратного распространения ошибки, в работе предложен метод применения генетического алгоритма для обучения нейронной сети, его суть состоит в обучении сети и получении положительного результата минимизации ошибки.
Генетический алгоритм является сочетанием градиентного и стохастического методов оптимизации функций. Регулируя вероятности кроссинговера и мутации можно достичь того, что алгоритм быстро найдет минимум. Однако этот минимум не гарантированно будет глобальным. Или же наоборот: алгоритм будет медленно спускаться к минимуму, но найдет глобальный минимум. Основным преимуществом генетического алгоритма является относительная простота его реализации. Недостатком – большое количество переменных параметров для управления его работой.
Предложенный в работе генетический алгоритм обучения сетей обратного распространения ошибки позволяет быстро произвести обучение системы с максимально умным значением функционала погрешности для каждой обучающей пары Emax=0,125.
Рецензенты:
Иваньков И.Н., д.т.н., доцент, доцент кафедры информатики Днепропетровского национального университета имени Олеся Гончара, г. Днепропетровск.
Ковалев М.А., д.т.н., доцент, доцент кафедры информатики Днепропетровского национального университета имени Олеся Гончара, г. Днепропетровск.
Библиографическая ссылка
Муниб М.Б. ИСПОЛЬЗОВАНИЕ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ ДЛЯ ОБУЧЕНИЯ СЕТЕЙ ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ // Современные проблемы науки и образования. – 2014. – № 1. ;URL: https://science-education.ru/ru/article/view?id=12210 (дата обращения: 21.11.2024).