Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Чернобровкин В.В. 1

---

1 ГБОУ ВПО Сургутский государственный университет

В статье рассматриваются методы повышения скорости вычислительных операций над многоразрядными числами с помощью системы остаточных классов или модулярной системы счисления. Приведено доказательство одного из вариантов китайской теоремы об остатках, лежащей в основе модулярного представления чисел. Образование цифр модулярного представления проводится независимо и каждый разряд несет информацию обо всем числе, что позволяет проводить параллельную обработку в независимых каналах, а также использовать новые методы арифметического контроля. Информация для обработки, представленная в виде вычетов, позволяет использовать исходные данные с большим или сверхбольшим количеством разрядов. Многоразрядные модулярные вычисления, применяемые для задач большой алгоритмической сложности позволяют периодически повышать производительность вычислительной техники.

Статья в формате PDF

273 KB

вычислительные операции.

вычеты

сравнения

Китайская теорема об остатках

Модулярная система счисления

1. Акушский И.Я., Юдицкий Д.М. Машинная арифметика в остаточных классах. – М.: Советское радио, 1968. – 440 с.

2. Бухштаб А.А. Теория чисел. – М: Наука,1977. – 368 с.

3. Виноградов И.М. Основы теории чисел. — М.: Наука, 1981. – 176 с.

4. Инютин С. А. Модулярные вычисления в сверх больших компьютерных диапазонах // Известия высших учебных заведений. – Электроника. – № 6. – 2001. – С. 81–87.

5. Инютин С. А. Вычислительные задачи большой алгоритмической сложности и модулярная арифметика // Вестник Тюменского государственного университета. – 2002. – № 3. – С. 14–23.

6. Коутинхо С. Введение в теорию чисел. Алгоритм RSA. – М.: Постмаркет, 2001. – 45 с.

7. Лобес М.В. Разработка методов и алгоритмов модулярных вычислений для задач большой алгоритмической сложности: дис. … канд. физ.-мат. наук. – Ставрополь, 2009. – 192 с.

8. Модулярные параллельные вычислительные структуры нейропроцессорных систем / Н.И. Червяков. – М.: Физматлит, 2003. – 43с.

9. Ноден П., Ките К. Алгебраическая алгоритмика. – М.: Мир, 1999. – 720 с.

10. Основы теории делимости чисел, решение уравнений в целых числах. Факультативный курс МГИЭТ (ТУ) / В.В. Бардушкин [и др.]. – М., 2003. – 100 с.

Введение

Основной стратегией теоретических и практических исследований, осуществляемых в настоящее время, является применение подходов, базирующихся на интенсивном использовании различных форм параллелизма на алгоритмическом, программном и аппаратном уровнях. В связи с чем исключительно большое значение имеют исследования, ориентированные на применение нетрадиционных способов кодирования числовой информации и соответствующих им параллельных вариантов компьютерной арифметики [6]. Возможность применения модулярной системы счисления [1–3,5–10] в вычислительных алгоритмах обусловливается наличием изоморфизма между математическими операциями над целыми числами и соответствующими операциями над системой целых неотрицательных вычетов по взаимно-простым модулям. Сложение, умножение, возведение в целую положительную степень целых положительных чисел сводятся к соответствующим операциям, выполняемым над множеством вычетов, – представлением этих чисел в модулярной системе счисления.

Целью исследования является исследование вопросов повышения скорости выполнения арифметических операций над многоразрядными числами с применением возможностей модулярной системы счисления, выявление зависимости объема обрабатываемых данных от нетрадиционных способов их представления и времени выполнения вычислительных операций с ними. Это является особенно важным при разработке алгоритмов для решения задач большой вычислительной сложности.

Методы исследования для решения поставленной задачи основываются на системном анализе, теории сравнений, теории чисел и алгоритмов, численных методах.

Фундаментом теоретико-числовой базой модулярной системы является теория сравнений, основы которой были разработаны Эйлером и отечественным математиком П.Л. Чебышевым. Применительно к обработке информации модулярными кодами теория опирается на следующее утверждение. Пусть А и р – два произвольных целых числа, причем р – положительное число, тогда в результате деления числа А на число р получаются частное и остаток [8]. Делимость А на р удовлетворяет равенству

(1)

и неравенству 0 ≤ α < p, (2)

где l – частное, α – остаток.

Согласно (1), величина а называется наименьшим неотрицательным вычетом [1, 3, 4–7, 8] целого числа А по модулю p и обозначается символом .

Для дальнейшего понимания вычислительных операций в модулярной системе проведем доказательство одного из вариантов китайской теоремы об остатках [2–4, 7, 10, которая является фундаментальным положением в основе модулярного представления чисел.

Теорема 1 (Китайская теорема об остатках). Любое целое положительное число A в модулярной системе счисления можно представить в виде набора остатков (вычетов) от деления этого числа на выбранные основания (модули) системы.

Доказательство.

Пусть число А представлено в системе остаточных классов следующим образом:

, (3)

где – наименьшие, неотрицательные вычеты, образованные путем целочисленного деления числа A на выбранные основания

, (4)

где – взаимно простые числа.

Если , , т.е. взаимно простые, то представление числа (3) является единственным, при условии

0 ≤ А≤ p. (5)

Тогда число A может быть представлено следующим образом:

;

; (6)

. . . . . . . . . .

;

Теорема доказана.

Формула (6) определяют сравнения, которые показывают, что каждый вычет ai получается независимо, а значит параллельно от других и содержит информацию обо всём числе. Данное обстоятельство определяет, если для таких вычислений организовать программно-аппаратную вычислительную базу, то вычеты могут образовываться параллельно.

Цифры ai представления (3) по выбранным модулям образуются следующим образом:

, (), (7)

где — целочисленное частное; – взаимно простые числа (основания системы).

Приведем пример, в котором рассмотрим кодирование чисел в модулярной системе счисления на конкретном примере. Пусть даны основания , , , тогда . Отображение всех тридцати чисел в системе оснований приведено в таблице.

Отображение чисел в системе остаточных классов

Как видно из таблицы, все остатки в модулярной системе одноразрядные, что дает преимущества для вычислительных операций перед обычной позиционной системой счисления (ОПСС), особенно если величина разрядов в числах значительно растет.

Над вычетами можно выполнять арифметические операции сложения, вычитания и умножения в кольце вычетов. Все они относятся к модульным операциям, то есть не требуют вычисления позиционных характеристик (ПХ) обрабатываемых чисел и поэтому считаются быстрыми.

Отношение сравнения по модулю натурального числа обладает следующими свойствами:

1) симметричность: ;

2) рефлексивность: ;

3) транзитивность: .

Множество вычетов по модулю натурального числа с двумя операциями обладает кольцевыми свойствами:

1) ассоциативность по сложению: ;

2) существование нулевого элемента: ;

3) существование обратного элемента:;

4) ассоциативность по умножению:;

5) дистрибутивность:.

Рассматривая вычисления в кольце вычетов с помощью модулярной арифметики все операции можно разбить на две группы. Пусть операнды А и В, а также результаты операций и представлены соответственно остатками , , , по основаниям , где (). Причём оба числа и результаты находятся в диапазоне [0, P], то есть

,;

;

(8)

При этом – кольцо целых чисел.

Так как выражение (8) является прямым следствием фактов теории чисел [2, 3, 5], то результаты аддитивной и мультипликативной операций можно переписать в виде

; , при . (9)

Если положить

, ,, (10)

то цифрами результата являются, соответственно,

;

; (11)

.

Выражения (11) могут быть получены на основании выражения (6).

Из вышеизложенного очевидно, что все вычислительные операции в кольце полностью распараллеливаются с помощью модулярной системы.

Перейдем к немодульной операции деления в модулярной системе. Если рассматривать представление (3) с условием , то операцию деления можно проводить в модулярной системе счисления поразрядно. Пусть числа А и В представлены по основаниям Тогда они будут иметь представления:

, , ,

Результат деления , (12)

где определяются как решения сравнения;

. (13)

Очевидно, что деление без остатка двух чисел в модулярной системе осуществляется путем модульного умножения делимого на мультипликативную обратную величину делителя.

Величина является решением сравнения

(14)

и однозначно определена, если и – взаимно простые числа.

Сравнения (13) имеют единственные решения в том случае, когда ; может принимать значение 0, поэтому от ограничения можно отказаться.

Если число А делится нацело на В, то представление (7) дает истинное значение для дроби С = , где С – некоторое целое число; если число А не делится нацело на В, то представление (7) будет формальным представлением дроби ; в этом случае .

Модульные операции и их результаты называются формальными, если при выполнении этих операций пренебрегают возможным выходом за пределы вычислительного диапазона.

Если А делится на В и среди цифр имеются нулевые значения, то из делимости А на В следует, что и . Таким образом, при поразрядном делении в i-м представлении (7) имеет место неопределенность типа, для раскрытия которой необходимо знание о всем числе [1].

Согласно китайской теореме об остатках все операции проходят по n каналам. Для этого построим параллельную вычислительную схему следующего вида (рис. 1):

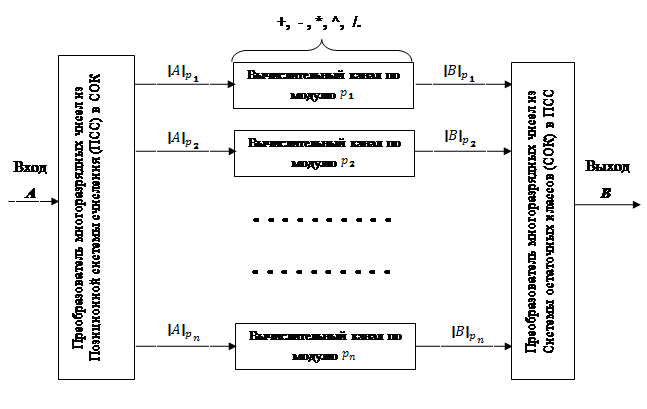
Рис.1. Обобщенная схема обработки многоразрядных чисел в модулярной системе

На схеме показано как А – входные многоразрядные данные – преобразуются на основе системы остаточных классов и подаются в n каналов обработки. Каждый из n каналов вычисляет по выбранному модулю (основанию) входные данные. Затем вычисленные значения поступают в «обратный» преобразователь и выходят в виде результата B.

На сравнительных графиках показана зависимость времени выполнения вычислительных операций от разрядности входных данных (рис. 2). Преимущества по времени и объему обрабатываемых данных при параллельной обработке возникают при следующих условиях:

1) разрядность обрабатываемых данных значительная;

2) количество и разрядность выбранных модулей (оснований) унифицированы под обрабатываемые данные.

Все вычислительные операции проводились на процессорах одного класса Intel Core2 Quad.

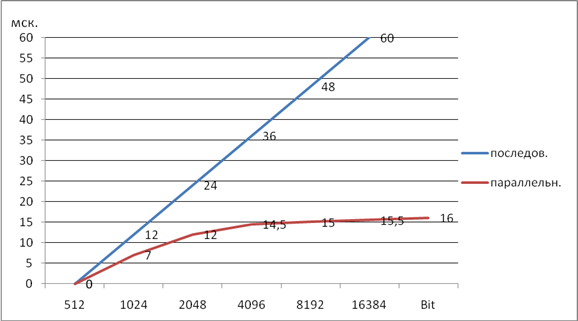
Рис. 2. Сравнительная схема выполнения вычислительных операций

На рис. 2 видно, что график при параллельной обработке данных похож на график функции y = log(x)и лежит ниже линейной зависимость последовательной обработки, что свидетельствует о преимуществах параллельной обработки на основе модулярного представления данных.

Выводы

1. Применение системы остаточных классов для вычислительных операций с многоразрядными данными дает значительное преимущество перед позиционными системами, так как имеет естественную по своей природе параллельность.

2. Вычисление цифр модулярного представления проводится независимо, и каждый вычет несёт информацию обо всём числе, что позволяет проводить параллельную обработку вычетов в независимых каналах и использовать методы арифметического контроля.

3. На основе модулярной системы представления данных возможны разработки параллельных алгоритмов для решения задач большой алгоритмической сложности.

Бахарев М.С., д.т.н., профессор, профессор кафедры «Нефтегазовое дело» Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Сургутский институт нефти и газа, (филиал) Тюменского государственного нефтегазового университета, г. Сургут.

Инютин С.А., д.т.н., профессор, профессор кафедры «Проектирование вычислительных комплексов» ФГБОУ ВПО «МАТИ – Российский государственный технологический университет им. К.Э. Циолковского (МАТИ)» г. Москва.

Библиографическая ссылка