Введение
Электротехнические устройства (ЭУ) (трансформаторы, реле, электромагниты, электродвигатели и т.п.) в своей конструкции содержат ферромагнитные магнитопроводы различной конфигурации и степени подвижности, одну или несколько катушек и другие вспомогательные элементы. Значит, в самом общем виде в качестве нагрузки для источников питания они могут быть представлены в виде катушки индуктивности с нелинейным магнитопроводом. Эксплуатационные характеристики ЭУ в значительной степени определяются магнитными свойствами магнитопровода. Таким образом, важной диагностической характеристикой ЭУ является вебер-амперная характеристика (ВАХ) магнитопровода, вид и параметры которой зависят от магнитных свойств ферромагнитного материала и конфигурации магнитной цепи.
Цель работы: разработка метода измерения ВАХ электротехнических устройств, позволяющая упростить процедуру измерения и обойтись без специальных средств измерений, при сохранении приемлемой точности.
Материал и методы исследований: методы теории планирования эксперимента, теории измерений, математического моделирования с использованием пакетов прикладных программ Microcap 9, Statistica 6.0.
Результаты и обсуждение.
Для получения ВАХ конкретного образца ЭУ необходимо воздействовать на магнитопровод внешним изменяющимся магнитным полем и измерять возникающий в его сечении магнитный поток. В большинстве случаев разборка диагностируемого ЭУ, недопустима, поэтому разработан ряд методов получения ВАХ [2], при которых в качестве источника внешнего магнитного поля используется катушка ЭУ, а информацию о потоке получают косвенным образом из уравнения цепи.
Недостаток этих методов – в том, что в их основе лежит операция интегрирования, кроме того, активное сопротивление катушки изменяется из-за нагрева. Необходимость нивелирования этих факторов инициировало ряд работ, в той или иной степени удачно решающих проблему [3, 4 ,5, 6]. Погрешность получения ВАХ этих методов составляет 5- 6%.
В общем случае ВАХ имеет вид гистерезисной петли, но так как в устройствах, работающих на переменном напряжении, используются магнитные материалы с узкой петлей гистерезиса, в большинстве практических случаев допустимо при расчетах использовать основную кривую намагничивания.
На наш взгляд, для решения задачи получения ВАХ магнитопровода конкретного ЭУ может быть использован метод натурно-модельного эксперимента (НМЭ). Известен положительный пример применения НМЭ в решении задач контроля и прогнозирования магнитных свойств изделий из ферромагнитных материалов [1]. Однако там требуются магнитоизмерительные приборы, что усложняет процедуру получения ВАХ.
В данной работе делается попытка решения задачи получения ВАХ на основе НМЭ и стандартных измерительных приборов (осциллограф, вольтметр переменного напряжения).
На рис.1 представлена функциональная схема такого устройства.
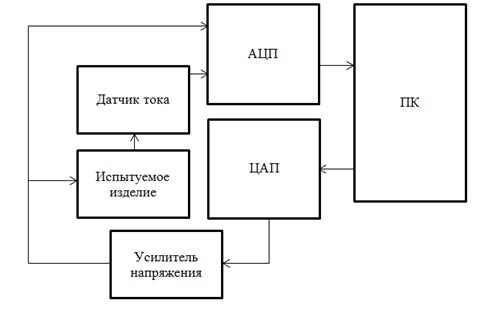
Рис. 1. Функциональная схема устройства для измерения ВАХ ЭУ
Работает оно следующим образом: к катушке ЭУ прикладывается синусоидальное напряжение U=Umsinωt (Um – амплитудное значение напряжения, ω – круговая частота). Это напряжение формирует персональный компьютер (ПК) в виде цифрового кода, который преобразуется при помощи ЦАП в аналоговый сигнал. С выхода ЦАП сигнал подается на усилитель напряжения. Значения тока через катушку ЭУ (с выхода датчика тока) и напряжения на ней подаются на вход АЦП, откуда поступают в ПК, где происходит вычисление, заданной в виде полинома, ВАХ по следующему алгоритму.
1. Измеряются амплитуда сигнала на выходе усилителя напряжения и координаты точек кривой тока через катушку ЭУ.
2. На вход математической модели ЭУ подают начальные значения параметров ВАХ и сравнивают измеренную и вычисленную кривые тока. Математическая модель ЭУ должна позволять по значениям параметров ВАХ и напряжению, подводимому к катушке ЭУ, вычислить координаты точек кривой тока.
3. В результате расчета по оптимизационному алгоритму определяют значения параметров ВАХ, при которых разность ΔS между измеренной и вычисленной кривыми тока минимальная.
Проиллюстрируем работу предложенного метода измерения ВАХ ЭУ, используя в качестве измерительного устройства модель, построенную при помощи пакета MicroCap, и математическую модель исследуемого ЭУ, построенную при помощи метода гармонического баланса, основанного на разложении функции в ряд Фурье. Использование модели измерительного устройства обусловлено возможностью задания в ней ВАХ магнитопровода ЭУ, что позволяет проконтролировать результат работы предложенного алгоритма.
На рис. 2. представлены временные диаграммы кривой тока через катушку и кривой напряжения подаваемого на катушку ЭУ.
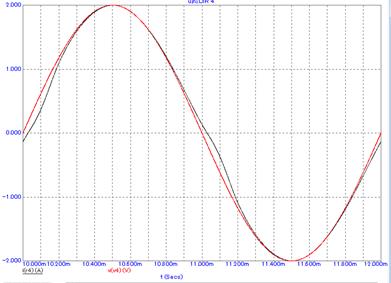
Рис. 2. Скриншот временных диаграмм работы модели
Построение математической модели ЭУ включает следующие этапы:
1. Запись уравнения состояния электрической цепи:
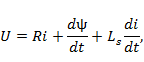
где ![]() – потокосцепление, w – число витков катушки ЭУ, Ф – магнитный поток, Ls – индуктивность рассеяния, R – активное сопротивление катушки.
– потокосцепление, w – число витков катушки ЭУ, Ф – магнитный поток, Ls – индуктивность рассеяния, R – активное сопротивление катушки.
Для реальных катушек индуктивности ЭДС, обусловленную потоками рассеивания, вследствие её малости, часто можно пренебречь, в результате чего выражение приобретает вид:

2. Выбор вида – выражение аппроксимации ВАХ сердечника нелинейной индуктивности.
Для большинства ферромагнитных материалов аппроксимирующее выражение зависимости тока от магнитного потокосцепления может быть задано следующим образом:
![]()
где a, b, c, d – коэффициенты аппроксимации.
3. Запись выражения для зависимости тока от времени с заданным числом гармоник:
![]() .
.
4. Построение математической модели ЭУ:
![]()
![]()
5. Нахождение аналитического решения для амплитуд гармоник тока:
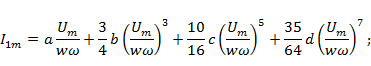
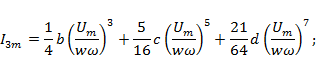
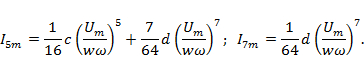
Для нахождения значений коэффициентов a, b, c, d (выбранных в качестве факторов) осуществляем построение при помощи ортогонального центрального композиционного планирования (ОЦКП) уравнение второго порядка поверхности отклика ΔS.
Обработка результатов эксперимента произведена при помощи пакета Statistica 6.0 (рис. 3).
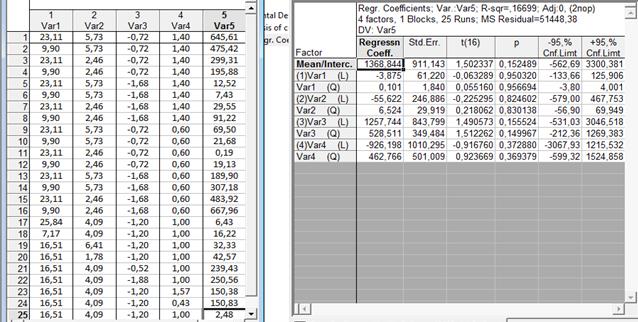
Рис. 3. Результаты расчета ОЦКП при помощи пакета Statistica 6.0
Получено уравнение регрессии второго порядка в физических значениях:
ΔS = 1368,844 - 3,875a + 0,101a2 - 55,622b + 6,524b2 +1257,744c + 528,511c2 –
- 926,198d + 462,766d2
Ниже представлены поверхности отклика при изменении различных сочетаний факторов (рис. 4. a-е).
а)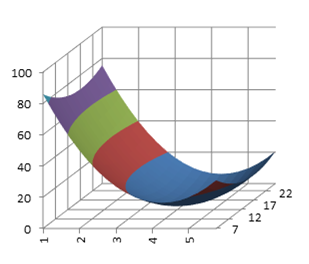 б)
б)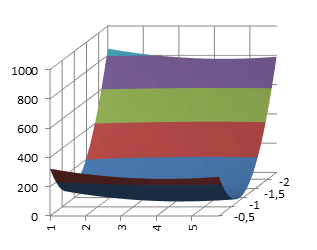
в)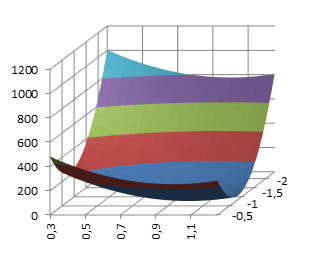 г)
г)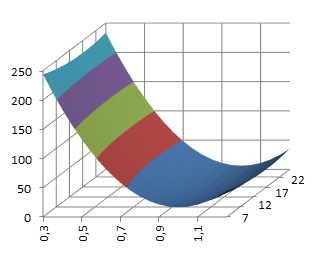
д)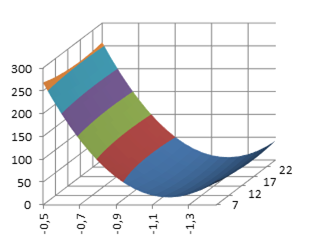 е)
е)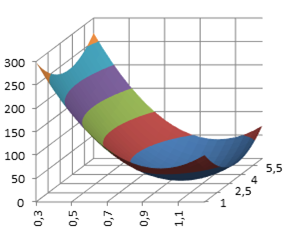
Рис. 4. Поверхность отклика: а – при изменении факторов a и b; б – при изменении факторов c и b; в – при изменении факторов c и d; г – при изменении факторов a и d; д – при изменении факторов a и с; е – при изменении факторов b и d.
Из анализа поверхностей откликов видно, что они имеют не более одного экстремума. Для нахождения коэффициентов аппроксимации может быть использован прямой метод оптимизации.
Сущность этого метода заключается в нахождении частных производных функции отклика по оптимизируемым параметрам, приравнивании их к нулю и решении полученных уравнений:
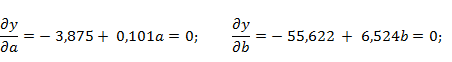
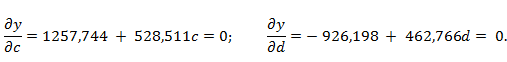
Для полученных значений факторов:
a = 1,918·105; b = 4,263·1016; c = -1,19·1028; d = 1,001·1039,
значение отклика в точке экстремума ΔS = 2,68.
Построим графики ВАХ магнитопровода ЭУ (рис. 5): образцовую из модели измерительного устройства и полученную методом нахождения точки экстремума поверхности отклика ΔS.
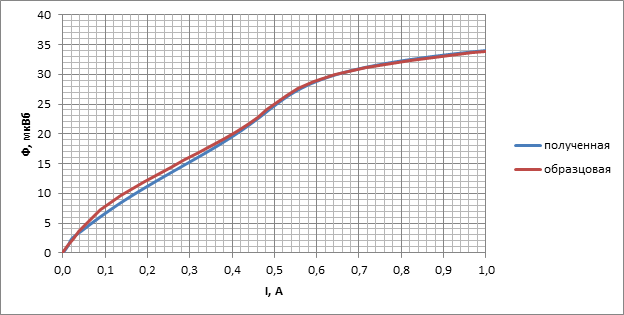
Рис. 5. Графики ВАХ.
Погрешность полученной характеристики найдем как проекции на оси 0I, 0Ф расстояния между образцовой и полученной кривыми:
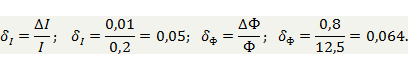
Вывод: Разработан метод измерения ВАХ, базирующийся на НМЭ, позволяющий обойтись без специальных средств измерений с сохранением приемлемой точности, которая составила 5% по току и 6,4% по магнитному потоку.
Рецензенты:
Кириевский Е.В., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова, г. Новочеркасск.
Лачин В.И., д.т.н., профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова, г.Новочеркасск.
Библиографическая ссылка
Ланкин А.М., Ланкин М.В. МЕТОД ИЗМЕРЕНИЯ ВЕБЕР-АМПЕРНОЙ ХАРАКТЕРИСТИКИ ЭЛЕКТРОТЕХНИЧЕСКИХ УСТРОЙСТВ // Современные проблемы науки и образования. 2014. № 1. ;URL: https://science-education.ru/ru/article/view?id=12186 (дата обращения: 26.02.2026).
DOI: https://doi.org/10.17513/spno.115-12186



