Введение
В работе моделируется преобразование акустического сигнала в электромагнитные сигналы (ЭМС) в слоистой диэлектрической среде. Акустические импульсы при своем распространении взаимодействуют с имеющимися и вновь возникшими дефектами [4]. В результате такого воздействия заряды или двойные электрические слои на границах раздела сред, включений или блоков, на бортах трещин или на других дефектах структуры диэлектрических материалов излучают электромагнитные сигналы [3]. Интенсивность излучения определяется вектором Умова – Пойнтинга [5]. Регистрация ЭМС в реальных условиях эксперимента осуществлялась с помощью емкостного датчика, который устанавливался около одной из граней образца [1, 2].
Методика
Методика расчетов такова, что в качестве исследуемой модели использовалась модель образца со слоистой диэлектрической структурой, который разделен на четыре равные части. Две крайние части имели плотность ρ=103 кг/м3, а средние части имели плотность 2·103 кг/м3 и 3·103 кг/м3 соответственно.
В данной работе производится расчет возникающих электромагнитных полей при произвольном расположении двух протяженных дефектов с двойными электрическими слоями, но с разным направлением распространения детерминированного акустического импульса. На рис. 1 показаны изолинии возникающего электромагнитного поля при взаимно перпендикулярном воздействии акустическим импульсом. Стрелками указаны направления возмущения акустическим импульсом эффективного поля.
а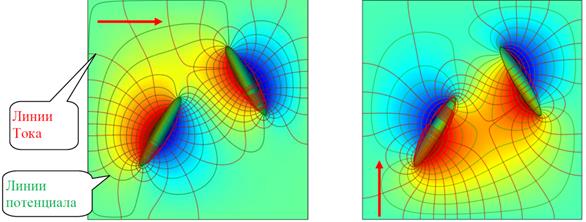 
б
Рис. 1. Распределение возникающего электромагнитного поля при взаимно перпендикулярном воздействии на образец с дефектами детерминированным акустическим импульсом: а) с частичным перекрытием дефектов; б) без перекрытия
В первом случае возбуждения образца дефекты частично перекрывают друг друга (рис. 1, а), а во втором случае (рис. 1, б) такого перекрытия дефектов относительно распространяющегося акустического воздействия нет. На рис. 1 представлены поля распределения потенциалов и токов. Наибольшей напряженности электромагнитного поля и величине токов смещения соответствуют области сгущения соответствующих им линий с большим градиентом. Видно, что при введении возбуждающего акустического импульса вдоль направления перекрытия дефектов (рис. 1, а) изолинии электромагнитного поля замыкаются в зоне перекрытия этих заряженных дефектов, а линии токов смещения разнесены. В этом случае амплитуда регистрируемого электромагнитного сигнала будет минимальной. При возбуждении акустическим импульсом в направлении без перекрытия дефектов (рис. 1, б) градиент токов смещения максимален. Здесь амплитуда электромагнитного сигнала за счет больших значений токов смещений будет возрастать при равных возбуждающих акустических воздействиях на образец с перекрывающимися дефектами.
Для выяснения влияния изменений зарядового состояния дефекта при возбуждении одинаковым акустическим импульсом, а также для определения влияния изменений амплитуды возбуждающего акустического импульса при постоянном зарядовом состоянии модельного дефекта проводились нижеследующие оценки. В качестве модели используется упрощенное представление заряженного дефекта. В образце имеется воздушная полость (трещина), с емкостью, определяемой соотношением:
, (1)
где: 
– ширина щели при отсутствии возмущения, 
Ф/м, 
м2, где 
-диэлектрическая проницаемость полости, 
– смещение сторон полости при внешнем возмущении. Наличие заряда 
на обкладках конденсатора означает наличие разности потенциалов 
. Пусть первоначальное значение напряжения равно 
, тогда уравнения для напряжения можно записать в виде:
, (2)
где 
– сопротивления образца.
Учитывая, что величина емкости конденсатора изменяется со временем из-за смещения пластины, обусловленного возмущением среды, используя (1) и (2), получим:
. (3)
Разрешая уравнение (3) относительно производной напряжения, получили:
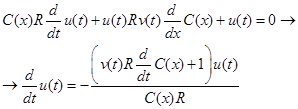. (4)
При известной величине напряжения 
можно определить заряд 
и ток смещения 
.
Используя соотношения:
. (5)
Будем считать, что деформация, вызванная акустическим возмущением, изменяется по колебательному закону. Тогда деформация запишется как 
, где 
– доля смещения относительно 
, а 
– скорость изменения деформации. В результате, используя (5), получим:
.
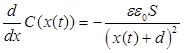Для решения дифференциального уравнения (4) использовался численный метод Рунге – Кутта [6] и выбирались следующие параметры среды: 
кОм – сопротивление среды, диэлектрическая проницаемость полости среды 
, а площадь поперечного сечения конденсатора равнялась м2. При этом значение емкости конденсатора 
Ф, определялось соотношением (1) при отсутствии возмущения.
Экспериментальная часть
Приведем решение двух задач:
Задача 1. В начальный момент времени задавали заряд на обкладках конденсатора 
и определяли изменение напряжения 
, заряда 
и тока смещения при внешних воздействиях, вызывающих смещение стенок полости, амплитуда которого составляет 
от ширины полости 
мм. Очевидно, что величина смещения пропорциональна величине внешнего возмущения, т.е. чем больше возмущение, тем больше отклонение от положения равновесия. Ниже на рис. 2 приведены графики смещения обкладок конденсатора 
и изменения емкости 
во времени, обусловленные внешним возмущением.
а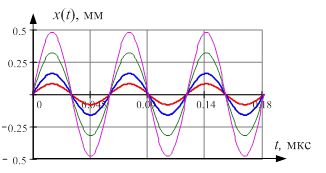
б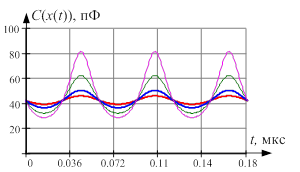 
Рис. 2. Расчетные значения изменений во времени при различном внешнем возмущении: а) смещения обкладок конденсатора ; б) емкости обкладок конденсатора 
Далее решали уравнение (1), используя метод Рунге – Кутта. Решения при начальном напряжении 
В приведены ниже, начальный заряд при этом равен 
(рис. 3, б).
а
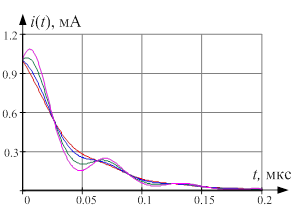б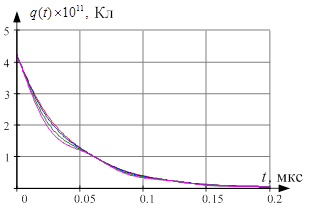 
Рис. 3. Расчетные значения изменений во времени при заданной величине заряда на обкладках конденсатора: а) тока смещения ; б) заряда
Расчет показал, что величины внешнего возмущения 
пропорциональны амплитуде отклика тока смещения в фиксированный момент времени.
Задача 2. В начальный момент времени задавались разные величины зарядов. При этом определялись изменения напряжения , заряда и тока смещения при одной и той же величине внешнего воздействия, вызывающего смещение стенок полости. Амплитуда смещение составляет 
от ширины полости d=1 мм.
а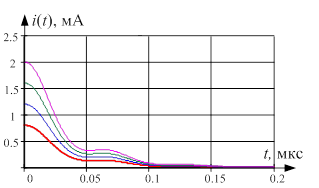
б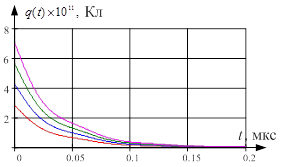 
Рис. 4. Расчетные значения изменений во времени при постоянном внешнем воздействии: а) тока смещения ; б) заряда
На рис. 4 приведены графики решения при начальных зарядах на обкладках конденсатора: 
, 
, 
, 
.
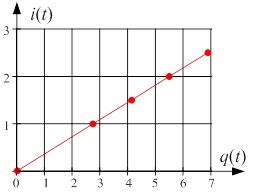
Рис. 5. Зависимость тока смещения от заряда в фиксированный момент времени в относительных единицах
Результаты расчета зависимости отклика системы, а именно – тока смещения от заряда в фиксированный момент времени в относительных единицах, приведены на графике выше (рис. 5). Во всех приведенных случаях внешнее воздействие одинаково и пропорционально смещению обкладок конденсатора.
Таким образом, произведено математическое моделирование следующих процессов:
- возбуждения электромагнитных сигналов импульсным акустическим воздействием;
- изменения параметров ЭМС при различном зарядовом состоянии диэлектрических дефектных структур;
- изменение параметров ЭМС при разных амплитудах акустического воздействия на дефектную структуру с постоянным зарядом.
Результаты
Расчеты по приведенным моделям показали, что в результате акустоэлектрических преобразований происходит переизлучение на двойных электрических слоях энергии воздействующих акустических импульсов в энергию электромагнитных откликов. Показано, что амплитуда ЭМС максимальна для не перекрывающихся дефектов относительно возбуждающего акустического импульса, а при пространственном перекрытии дефектов структуры относительно направления распространения акустического импульса амплитуда ЭМС уменьшается до минимума. Установлено, что изменение амплитуды ЭМС линейно зависит от величины заряда на обкладках дефекта, так же как и от величины возбуждающего акустического импульса при постоянном зарядовом состоянии дефекта.
Рецензенты:
Канев Ф.Ю., д.ф.-м.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Васильева О.В., Исаев Ю.Н. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ АНАЛИЗА ПЕРЕИЗЛУЧЕНИЯ АКУСТИЧЕСКИХ ИМПУЛЬСОВ В ЭНЕРГИЮ ЭЛЕКТРОМАГНИТНЫХ ОТКЛИКОВ ДЕФЕКТНЫХ СТРУКТУР // Современные проблемы науки и образования. – 2014. – № 1. ;URL: https://science-education.ru/ru/article/view?id=12181 (дата обращения: 23.04.2024).