Введение
Создание материалов для экстремальных условий эксплуатации требует не только разработку новых составов повышенной эффективности, но и прогнозирования поведения таких материалов в различных условиях эксплуатации. Важным вопросом является также определение оптимального соотношения компонентов и оптимальных физико-химических параметров самих материалов [3, 5]. Решение этой задачи возможно при имитационном математическом моделировании поведения материалов с учетом множества воздействующих параметров и физико-химических характеристик материалов в достаточно широком диапазоне. Применение новых компонентов делает имитационное моделирование особенно необходимым. Существенный вклад в формирование свойств многокомпонентных материалов вносят наполнители. Функцией наполнителей обычно является улучшение механических свойств (прочности, твердости и др.). В экстремальных условиях эксплуатации – при температурах вблизи и выше температуры работоспособности материала некоторые наполнители могут играть стабилизирующую роль при температурном разрушении материала. Как показали наши исследования, к таким наполнителям относятся функционально-активные наполнители, в частности перлит и карбид кремния [2, 6-8]. Так, карбид кремния диссоциирует при весьма высокой температуре (более 2500 оС) с поглощением большого количества тепла. Это делает его перспективным функционально-активным наполнителем – своего рода эндотермической добавкой в слоях полимерного материала, подвергающихся действию пламени.
Однако поведение таких материалов при высокотемпературных воздействиях было исследовано недостаточно. Так как исследуемые полимерные эластомерные являются многокомпонентными и их характеристики могут быть варьированы в широком диапазоне, то целесообразным является применение многофакторного моделирования.
Эффективность огнетеплозащитных материалов (ОТЗМ) на основе каучуков определяется комплексом эндотермических физико-химических превращений: плавлением, кипением и сублимацией компонентов и их термодеструкцией, пиролизом, нагревом газов пиролиза и их вдувом в коксовый слой и поверхностную зону, а также процессами изменения химической структуры материала – вспучиванием, порообразованием, коксованием. Совокупность физико-химических и структурных превращений в материале, а также низкая тепло- и температуропроводность ОТЗМ на основе многокомпонентных резин, обеспечивает эффективное выполнение функции теплозащиты. Большая доза тепла расходуется на распад химических связей с выделением низкомолекулярных продуктов и нагрев этих продуктов до высокой температуры. Доля энергии, приходящаяся на собственно пиролиз, составляет до 28–35 %, т.е. в среднем около одной трети в общей энтальпии нагрева с 293 до 1273 К.
Математическому описанию процессов нестационарного прогрева различных ТЗМ, в том числе в условиях термического и эрозионного разрушения материала, посвящен ряд работ [4, 9, 10]. Значительно меньше работ посвящено эластомерным ТЗМ, в которых наряду с нестационарным прогревом, термическим и эрозионным разрушением материала большое значение приобретают процессы резкого изменения физической и химической структуры и деформационные процессы, в частности процесс вспучивания. Существенно осложняет математическое описание образования пенококса на поверхности ТЗМ.
Анализ различных расчетных формул и математических моделей показал, что в условиях высокотемпературного нагрева и вспучивания материала наиболее полно поведение ОТЗМ описывается моделями, предложенными в работах [4, 9]. Целесообразность математического моделирования обуславливается также необходимостью сокращения дорогостоящих экспериментов, также повышением надежности прогнозирования работы и выбором минимально необходимой толщины ТЗМ.
Целью исследования было проведение многофакторного имитационного математического моделирования поведения огнестойких эластомерных материалов с микродисперсным карбидом кремния при воздействии высокотемпературных тепловых потоков.
Материалы и методы исследования
Объектом исследования являются вулканизаты на основе бутадиенстирольного каучука СКМС-30АРКМ15 и этиленпропилендиенового каучука с серной вулканизующей группой (стандартные резиновые смеси) [1]. Смеси готовились на лабораторных вальцах 160х320мм. Вулканизация образцов проводилась при температуре 145 оС.
Для исследования использовался микродисперсный карбид кремния SiC с размерами частиц 10-50 мкм. Молекулярная масса (ва. е.м.): 40,1. Температура плавления (в °C): 2830 Температура разложения (в °C): 2830. Плотность: 3,22 (20°C, г/см3). Энтальпия образования ΔH: -1648,3 кДж/кг, стандартная мольная теплоемкость Cp (298 К, Дж/моль·K): 26,86 (т); теплопроводность – 490(Вт/(см·К).
Кроме того, в составы вводился наполнитель БС-120 – аморфный диоксид кремния SiO2 с удельной поверхностью 120м2/г и средним размером частиц 20 нм. Плотность SiO2 равняется 2,648 г/см³. Вещество плавится в пределах температур от 1600 до 1725 °С, кипит при температуре 2230 °С.
Высокотемпературное воздействие на материал осуществлялось с использованием открытого пламени горелки плазмотрона (температура воздействия до 3273К).
Результаты исследования
Основной целью излагаемых ниже расчетов является выявление на тематических моделях пределов изменения теплофизических характеристик при варьировании физико-химических параметров материала достигаемых за счет изменения состава и структуры. Это позволяет оценить целесообразность поисков в данном классе материалов и выявить наиболее значимые факторы при различных режимах нагрева. Кроме того, автором проведено уточнение некоторых расчетных формул с учетом реально протекающих процессов. Выявление важной роли предпиролизного слоя потребовало введения новых моделей, более точно описывающих процесс прогрева. Исходным соотношением для математической модели является баланс энергии на фронте коксования
 (1)
(1)
где λК и λ0 – теплопроводность кокса и ТЗМ, ρ0 – исходная плотность, ξ – координата, связанная с текущим положением рабочей поверхности, ς – координата, связанная с фронтом коксования, δК – толщина коксового слоя, К – коксовое число, QΣ – тепловой эффект пиролиза, ε – относительное изменение объема при вспучивании, υy – скорость движения рабочей поверхности.
Математическая модель строится на основании физической модели вспучивающегося ТЗМ. ОТЗМ в этой модели из вспучивающегося кокса и деструктурирующегося эластичного материала. В результате вспучивания рабочая поверхность двигается в сторону источника тепла, а граница пиролиза (коксования) двигается вглубь материала. Таким образом, распределение температур определяется двумя взаимозависимыми переменными, изменяющейся толщиной и временем, т.е. реализуется автомодельный режим прогрева.
Общая толщина ОТЗМ будет определяется формулой:
δ = δд+ δпр, (2)
где δпр и δд – глубина прогретого и продеструктируемого слоя.
Для имитационного моделирования использовался специальный программный комплекс «Тепло» [4]. Программа «Тепло» позволяет определить зависимость величины прогрева (коэффициентов деструкции, толщин деструкции, прогрева и необходимой толщины ОТЗМ) от 15 параметров. Программа позволяет найти экстремум функции δ (общей толщины ОТЗМ) и функциональные зависимости δ,δд,δд от деформации вспучивания, теплопроводности кокса, теплового эффекта пиролиза.
Все это позволяет провести достаточно полное имитационное моделирование процесса прогрева (вычислительный эксперимент).
Рассмотрим зависимость выходных характеристик ОТЗМ от отдельных параметров при температуре воздействующего потока 1273К. Воздействующие факторы будем изменять в широких пределах, захватывая возможные интервалы их варьирования от минимально возможного до максимально возможного в реальных материалах.
Имитационное моделирование показывает, что повышение температуры пиролиза полимерной матрицы ОТЗМ Тк, приводит к тому, что увеличивается относительная толщина недеструктируемого материала (рисунок 1). Однако из-за того, что прогрев в отсутствии деструкции идет быстрее, то увеличивается δпр.
С другой стороны, увеличение Tк уменьшает глубину деструкции δд, что может привести к увеличению параметра эффективности, определяемого методом удаления коксового слоя. При этом общая толщина ТЗМ одинаково возрастает.
Таким образом, одним из важных и необходимых следствий является необходимость организации процесса коксования при более низких температурах. Это увеличит роль эндотермических физико-химических превращений в ТЗМ. Этот вывод применим к ТЗМ, у которых невелика толщина вспучивающегося предпиролизного слоя резины, снижающего скорость прогрева подкоксового слоя.
Наилучшим вариантом с точки зрения минимальной толщины ТЗМ будет вариант с минимальным значением Tк и максимальным значением εв. Для минимизации толщины материала необходимо увеличивать Тк при одновременном увеличении εв. Таким образом, в отношении влияния величины Тк выявлено техническое противоречие. Как видно из рисунка 1, компромиссное решение по оптимизации обоих параметров находится в области 673 К. Полученные при вычислительном эксперименте выводы позволяют более обоснованно выбирать каучуковую основу ТЗМ в зависимости от параметра оптимизации.
Компоненты, на основе которых можно создавать ТЗМ, имеют достаточно широкий диапазон теплофизических и физико-химических характеристик. Так, температура пиролиза каучуков находится в интервале 553–723К, теплота пиролиза 0,5–1,5 МДж/кг, температура порообразования зависит от введенных пластификаторов и других органических компонентов, температура кипения или разложения которых колеблется в интервале 423–723 К и выше. Теплоты кипения большинства пластфикаторов лежат в интервале 900–270кДж/кг. Как показано ниже, теплота испарения и разложения некоторых добавок может превосходить теплоту пиролиза каучука.
На рисунке 2 приведены зависимости выходных параметров от теплоты пиролиза. Как видно, наиболее чувствительна к изменению теплоты пиролиза δд. Величина δ наиболее сильно изменяется в интервале 0–2 кДж/кг. Дальнейшее увеличение практически не приводит к изменению δ. Следует отметить, что указанный интервал относится к практически регулируемым рецептурными факторами величинам теплоты пиролиза. Так, введение наполнителей, разлагающихся с высокой теплотой разложения или кипения в высокотемпературной области, позволяет повысить общую теплоту пиролиза материала с 1200 кДж/кг до 1540кДж/кг, то есть почти на 30 %. Это позволит уменьшить необходимую толщину материала на 12–15 %.
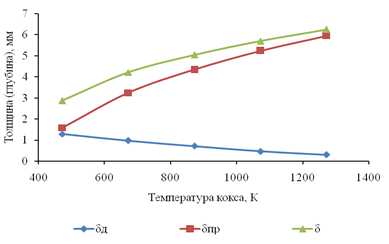
Рисунок 1. Зависимость толщины ТЗМ (δ), глубины прогрева (δпр) и деструкции (δд) от температуры кокса (Тпов = 1273 К, деформация вспучивания εВ= 0,6)
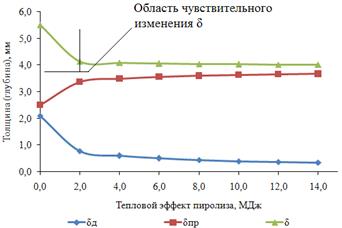
Рисунок 2. Зависимость толщины ТЗМ (δ), глубины прогрева (δпр) и деструкции (δд) от теплового эффекта пиролиза (QΣ)
В целом следует отметить, что изменение величины теплового эффекта за счет рецептурных факторов может привести к весьма существенному изменению δд, особенно при невысоких значениях коксового числа.
В этой связи роль образования коксового слоя выглядит не однозначно. При высоких температурах и низком эрозионном уносе материала, более выгодно, чтобы весь материал термически деструктурировался с большим поглощением тепла. Высокая теплопроводность кокса и его высокая температура приводят к тому, что такой кокс слабо защищает недеструктируемый слой, т.к. граница пиролиза быстро продвигается внутрь материала.
С другой стороны, вспучивание кокса оказывает существенное влияние на теплозащитную способность, и оба эти фактора (QΣ и εв) нужно рассматривать как синергические. Действительно, одно увеличение QΣ с 0,3 до 3∙106кДж/кг позволяет уменьшить δд в 1,84 раза, увеличение εв с 0,2 до 0,6 в 1,27, а одновременное увеличение обоих этих факторов увеличивает δд в 2,15 раза.
Выводы
Таким образом, анализ математической модели показывает возможность существенного улучшения теплозащитных характеристик материала за счет одновременного увеличения теплового эффекта пиролиза и вспучивания кокса.
Рецензенты:
Шиповский И.Я., д.т.н., профессор, Волжский политехнический институт (филиал) ФГБОУ ВПО «Волгоградский государственный технический университет» (ВПИ (филиал) ВолгГТУ), г. Волжский.
Носенко В.А., д.т.н., профессор, заведующий кафедрой «Технология и оборудование машиностроительных производств», заместитель директора по учебной работе, Волжский политехнический институт (филиал) ФГБОУ ВПО «Волгоградский государственный технический университет» (ВПИ (филиал) ВолгГТУ), г. Волжский.
Библиографическая ссылка
Лифанов В.С., КАБЛОВ В.Ф., НОВОПОЛЬЦЕВА О.М., Кочетков В.Г. МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ ОГНЕСТОЙКИХ ЭЛАСТОМЕРНЫХ МАТЕРИАЛОВ С МИКРОДИСПЕРСНЫМ КАРБИДОМ КРЕМНИЯ ПРИ ВОЗДЕЙСТВИИ ВЫСОКОТЕМПЕРАТУРНЫХ ТЕПЛОВЫХ ПОТОКОВ // Современные проблемы науки и образования. 2014. № 1. ;URL: https://science-education.ru/ru/article/view?id=12177 (дата обращения: 08.02.2026).



