Введение
В работе [2] автором были описаны некоторые методы, позволяющие применить математический аппарат аппроксимации поверхностей сплайнами (см. [1]) особой конструкции, что, в свою очередь, позволяет довести такие методы до практического применения в области механической обработки материалов. Учитывая, что в последние десятилетия компьютерные и информационные технологии в аппаратной части способствовали созданию таких новых инструментов как 3D-печатающие устройства (или 3D-принтеры), потребность в развитии математических основ аппроксимации поверхностей и применения разработанных ранее методик обрела вполне осязаемый смысл. В данной статье опишем также основные классы пригодных для 3D-печати методов сплайнирования (т.е. приближения соответствующими сплайнами), являющиеся вполне применимыми в условиях существующих аппаратно-программных комплексов и технологий.
Сплайны функций одной переменной
Напомним, что (плоским) сплайном некоторой функции одного вещественного переменного ![]() обычно называют составную функцию
обычно называют составную функцию ![]() , являющуюся набором элементов или компонент, являющихся в свою очередь функциями определенного класса или порядка (например, отрезки прямых, параболы 2-го или 3-го порядка и т.д.), которыми аппроксимируется исходная функция
, являющуюся набором элементов или компонент, являющихся в свою очередь функциями определенного класса или порядка (например, отрезки прямых, параболы 2-го или 3-го порядка и т.д.), которыми аппроксимируется исходная функция ![]() Подробно сама теория сплайнов и ее применения разобраны в книге [1].
Подробно сама теория сплайнов и ее применения разобраны в книге [1].
Обычно порядок компонентов определяет и порядок всего сплайна (второй при аппроксимации квадратными параболами, третий – при кубических параболах и т.д.). При этом отрезок ![]() , на котором задана аппроксимируемая функция, разбивается на ряд подсегментов, например,
, на котором задана аппроксимируемая функция, разбивается на ряд подсегментов, например, ![]() , а сами компоненты сплайна задаются определенным способом над этими участками и итоговый сплайн представляет собой составную функцию:
, а сами компоненты сплайна задаются определенным способом над этими участками и итоговый сплайн представляет собой составную функцию:
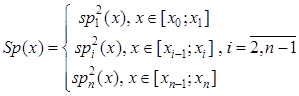 ,
,
где верхний индекс указывает на порядок аппроксимирующей функции-компоненты. Недостатком такого способа создания сплайнов является наличие потери гладкости в узловых точках. Существуют определенные способы наложения дополнительных условия для исправления такого недостатка (привязка по производным в узловых точках), но следует отметить, что все это значительно "утяжеляет" всю конструкцию и счет.
Определенным расширением возможностей построения сплайнов является иной метод составления аппроксимирующих функций. Рассмотрим аппроксимацию обычными кривыми второго порядка (квадратными параболами), при которой, например, параболы «проводятся» по тройкам точек (для кубических аппроксимаций используются четверки точек и т.д.). В этом случае над каждым из подсегментов (кроме крайних) получается в результате по паре аппроксимирующих парабол (для кубического случая по тройке кубических парабол за исключением пар крайних точек). В качестве итоговой сплайн-функции можно взять: a) средние арифметические парабол, b) среднее геометрическое пар парабол, c) средневзвешенное (например, среднеквадратическое значение определенного вида или же итоговое значение на участке с определенными весами) и т.д. Такие сплайны будем называть усредненными, указывая при этом дополнительно их тип (например, усреднено-арифметическими, усреднено-геометрическими, усреднено-квадратичными, усреднено-взвешенными и т.д.). В сравнении с предыдущим способом построения, усредненные сплайны имеют лучшую аппроксимацию а как нетрудно доказать, определенным образом (хотя и ступенчато) сглаживают некоторые точки исходной аппроксимируемой функции (например, точки ее перегиба).
Рассмотрим пример усредненного (метод усреднения опущен) гиперболического сплайна (см. ниже):
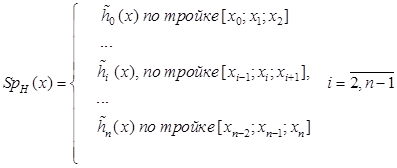 . (1)
. (1)
Далее, в качестве компонентов сплайн-функций можно взять отрезки эллипсов:
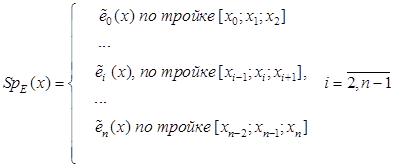 . (2)
. (2)
Здесь волна над компонентами сплайнов (1) и (2) означает некоторый способ усреднения (см. выше), не указанный явно.
Подводя промежуточный итог, отметим, что идея сплайн-аппроксимации нужного результата сама по себе издревле применялась человеком при обработке: сюда можно отнести копирование изображений «по клеточкам», обработку древесины и резьбу по ней, гончарные ремесла, механическую шлифовку лопаток турбин и т.д. Но задача, которая интересует нас в большей степени, это возможности переносов сплайн-методов на пространственные случаи, а также те классы аппроксимирующих функций, которыми люди располагают при использовании разнообразных режущих инструментов, приспособлений и различных технологий резки, включая лазерную технику.
Классы HYP и ELL
В связи с последним, нам представляется вполне логически оправданным рассмотреть один из нескольких классов «удобных» 3D-поверхностей, в частности это те, которые могут быть образованы перемещением прямых или отрезков прямых в трехмерном пространстве, которые в наиболее простом случае считают линейчатыми. Примерами таких поверхностей являются различные конусы (круговые, эллиптические и иные), а также гиперболические поверхности, например однополосной гиперболоид или гиперболическое седло, хотя более сложные случаи не ограничиваются только такими поверхностями. Учитывая важную роль в этом классе гиперболических поверхностей, будем далее называть его ![]() , подразумевая, что дополнительные индексы используются для ограничения класса до нужных параметров.
, подразумевая, что дополнительные индексы используются для ограничения класса до нужных параметров.
Второй класс интересующих нас поверхностей был нами назван ![]() по сокращению формирующего такие поверхности класса эллиптических кривых. Представители этого класса могут быть получены за счет, например, линейчатого движения прямой или отрезка по эллиптической (в частности, круговой) направляющей.
по сокращению формирующего такие поверхности класса эллиптических кривых. Представители этого класса могут быть получены за счет, например, линейчатого движения прямой или отрезка по эллиптической (в частности, круговой) направляющей.
Возвращаясь к методам обработки материалов, приведем не претендующее на полноту описание типичного инструментария для обработки материалов (и, в частности, создания форм): токарные, фрезерные, гидроструйные, лазерные установки, электро- и газоплазменные установки, комплексные установки, 3D-принтеры. Технологии обработки в этом случае прямо указываются в определении. Следует сразу отметить здесь же, что мы считаем необходимым дополнить этот ряд такими устройствами, опубликованное описание которых нам неизвестно, но смысл их технологическое действия может быть достаточно детально объяснен, как 3D-плоттеры (как наращивающие некоторую печатаемую модель, так и режущие или формирующие результат из материала). Во многих из перечисляемых устройств инструментальная часть является либо вращающейся, либо имеет перемещение по прямой или иной направляющей. В случае, например, гидроструйных устройств результат может быть получен при помощи управления инструментом, производимым компьютерным устройством напрямую из программного обеспечения класса AutoCAD (источником модели детали может быть обычный dwg-файл).
В силу специфики предлагаемых автором методов математического описания инструментов (и потому технологий), можно разделить их на гиперболические и эллиптические.
Гиперболические инструменты
Примером гиперболического инструмента может являться гипотетическая лазерная установка резания, имеющая управление перемещения луча по направляющей прямой и создающая в результате эффект гиперболического седла. Другой пример: обрабатываемая модель имеет поступательное (и даже круговое) движение, а режущий луч перемещается вдоль материала с возможностью поворота после каждого прохода на определенный угол. Ясно, что эти элементарные примеры не описывают все возможности гиперболических инструментов, например даже один из простейших таких инструментов – гиперболическая фреза – может быть легко создан особым способом заточки обычных фрез так, чтобы их прямая режущая кромка находилась под определенным углом к оси вращения самой фрезы. Таким образом, получается вполне понятный набор механических средств и инструментов для получения поверхностей достаточно сложной формы. Отметим здесь же, что главным условием для возможности применения гиперболического инструмента является выпуклость требуемой поверхности, но, в то же время, получение гиперболического седла представляет собой возможности достижения аппроксимации и выпукло-вогнутых участков поверхностей.
Эллиптические инструменты
Эти инструментальные возможности также могут быть довольно элементарно проиллюстрированы с использованием фрезы: если вращающаяся торцевая фреза вырабатывает материал, перемещаясь по нему не под прямым углом, то получающийся в результате след выборки будет иметь в поперечнике эллиптическое сечение. Еще одним технологическим способом получения эллиптической линейчатой поверхности является применение эллиптического циркуля (или эллипсографа), у которого вместо рисующей точки установлен лучевой режущий инструмент. Общим моментом применимости различных эллиптических инструментов является задача обработки вогнутой поверхности.
Вернемся к вопросам сплайнирования для аппроксимации некоторой 3D- поверхности. Будем считать, что она задана условием:
![]() .
.
Тогда аппроксимирующая функция (точнее будет называть ее инструментом) определяется способом выработки (или формирования) материала. Если выработка представляет собой линейчатую поверхность класса ![]() , то, исходя их двух составных направляющих:
, то, исходя их двух составных направляющих:
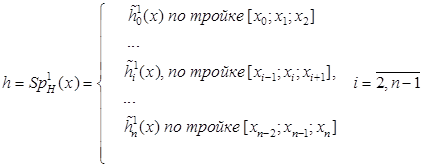
и
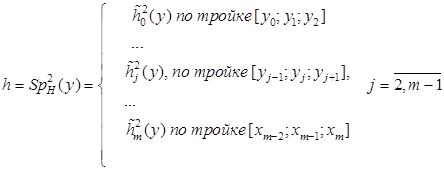 ,
,
и учитывая характер конкретной поверхности, может быть создан алгоритм обработки, проводимой под компьютерным управлением из файла данных через активаторно-контроллерный интерфейс ПК и установки.
3D-плоттинг
Вернемся теперь к уже упомянутым выше принципам возможного 3D-плоттинга, но рассмотрим вначале двумерный аналог такого плоттирования. Наиболее простой и распространенный набор примеров действия обычных плоттеров – создание контурных карт и чертежей. Само устройство (плоттер) состоит из координатных двигателей и приводящего механизма чертящего блока (или пера в одноцветном случае) для вычерчивания тех или иных кривых. Наш смысл развития идеи плоттинга на случай 3D состоит из двух обобщений: первый метод (и самый простой) состоит в том, что прямоугольная рамка устройства координатного смещения плоттера, перемещающего перо, получает 4 разных уровня фиксированного подъема каждого угла над моделируемой поверхностью, а само перо работает как экструдер на выпуск того или иного пластического (и застывающего под действием света, температуры, ультрафиолетового излучения или влажности) «строительного» материала. В результате получается некий «седловой» (гиперболический) плоттер, который может наносить послойно формирующий материал на некую подложку. Отметим сразу, что вместо пера или экстрагирующего устройства на головке такого 3D-плоттера может быть установлен режущий, плавящий, или удаляющий материал иным способом инструмент (вплоть до отдельного бора или фрезы; тогда можно рассмотреть вариант создания моделей удалением материала, что обратно наращиванию).
Второй метод 3D-плоттинга состоит в том, что вся рамка с таким пером получает зависимый (от плоских горизонтальных координат) способ передвижения по третьей координате – высоте, но, в отличие от 3D-принтера, объемная печать идет не точечным способом, но по прямым, кривым, отрезкам, ломаным и т.п. Отличие такого способа 3D-конструирования заключается в разнице, которую имеет, скажем, векторная компьютерная графика в сравнении с обычной растровой.
Рецензенты:
Авхадиев Ф.Г., д.ф.-м.н., профессор, зав. кафедрой, теории функций и приближений, КФУ, г.Казань.
Гурьянов Н.Г., д.ф.-м.н., профессор, кафедра общей математики, КФУ, г.Казань.
Библиографическая ссылка
Тагиров Т.С. О КЛАССАХ HYP И ELL И СПЕЦИАЛЬНЫХ СПЛАЙН-ФУНКЦИЯХ ДЛЯ 3D-МОДЕЛИРОВАНИЯ ПОВЕРХНОСТЕЙ // Современные проблемы науки и образования. 2014. № 1. ;URL: https://science-education.ru/ru/article/view?id=12164 (дата обращения: 08.02.2026).



