Проблемы решения задач в широком смысле этого слова являются предметом исследования многих наук: философии, психологии, педагогики, логики и частных методик. Как сделать обучение максимально развивающим мышление, все познавательные способности учащихся, как научить их мыслить – вот те вопросы, которые стоят в центре большинства дидактических исследований. В качестве основных параметров, оказывающих развивающую функцию в обучении, мы рассмотрели логическую правильность постановки задачи и степень ее определяемости.
Типология таких задач включает в себя задачи с избыточным, с неполным и противоречивым условием.
1. Задачи с избыточным условием – задачи, в которых имеются лишние данные, не нужные для решения, а лишь маскирующие необходимые для решения задачи данные.
2. Задачи с неполным составом условия – задачи, в которых отсутствуют некоторые данные, необходимые для решения задачи, вследствие чего дать конкретный ответ на вопрос задачи не всегда представляется возможным.
3. Задачи с противоречивым условием – задачи, содержащие в условии противоречие между данными. Примеры таких типов задач:
1. Задача с избыточным условием: Точки А,В,С лежат на окружности с центром в т. О, ∠ АВС = 50°, ∪ АВ: ∪ СВ = 5:8. Найти ∠ АОС.
2. Задача с неполным условием: На протяжении 155 м уложены трубы (25 штук) длиной по 5 м и 8 м. Сколько уложено тех и других труб?
3. Задача с противоречивым условием: В двух сараях сложено сено, причем в первом сарае сена было в 3 раза больше, чем во втором. После того как в первый сарай привезли 20 т, а из второго взяли 10 т, в обоих сараях сена осталось поровну. Сколько всего сена было в двух сараях первоначально? (Из меньшего взяли, а в большее добавили, и стало одинаково, такого быть не может, ответ противоречит здравому смыслу.)
Анализируя школьные учебники, мы убедились, что практически ни один из них не содержит задач такого типа. Проводя эксперименты с учащимися, было видно, что, столкнувшись с такой задачей, ученик затрудняется ее решить. Все это потому, что решению задач уделяется большее внимание, чем анализу самих решаемых задач. Одной из главных причин тех методических затруднений, которые испытывает учитель при обучении решению задач, является отсутствие анализа задачи с точки зрения их определяемости и в связи с этим – неумение видеть внутреннюю структуру задачи, неумение видеть процесс образования задачи.
В частности выясняется, что аномальные задачи следует предлагать в следующей последовательности: начинать следует с введения задач переопределённых, предупреждая на первых порах учащихся о наличии избыточных данных и предлагая им найти такие данные, постепенно переходя от задач простых к таким задачам, в которых избыточные данные не сразу бросаются в глаза.
Когда учащиеся приобретут некоторые навыки решения таких задач, можно перейти к введению таких задач уже без предупреждения о наличии избыточных данных, чередуя эти задачи с традиционными определёнными задачами. Таким образом, не зная, имеется ли в условии задачи лишнее данное или нет, но подозревая, что оно может быть, учащиеся к каждой задаче будут подходить критически, что вызовет большую, чем в традиционных условиях, необходимость внимательного анализа условия задачи и различных подходов к её решению.
На некотором этапе переопределённые задачи, предлагаемые учащимся, могут стать противоречивыми. Использование таких задач постепенно приучит их к тому, что обнаруженное в условии лишнее данное не следует игнорировать, но следует проверять его на противоречивость.
Рассмотрим методику работы с моделью задач с неполным, с избыточным и противоречивым условием, и составим план их решения.
Займемся сначала задачей с неполным условием: В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 6 см дальше, чем от большей стороны. Найти длину сторон. (Необходимо знать еще одну величину, например, периметр прямоугольника.) І. Осмысление условия
В: О какой фигуре идет речь в задаче?
О: О прямоугольнике.
В: Что должно быть построено в прямоугольнике?
О: Диагонали.
В: Что нам известно о точке пересечения диагоналей?
О: Она отстоит от меньшей стороны на 6 см дальше, чем от большей стороны.
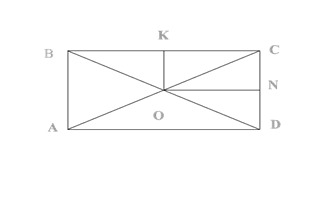
Запишем условие:
Дано: ABCD прямоуг.
OK< ON на 6 см
Найти: стороны
прямоугольника
II. Поиск пути решения
В: Что нужно найти?
О: Стороны прямоугольника.
В: Что следует из того, что OK< ON на 6 см?
О: ON – OK = 6
В: Давайте ОК обозначим за х. Чему тогда равно ON?
О: х + 6
В: Можем ли мы, используя наши обозначения, выразить
сторону АВ?
О: Да, т.к. ОК это половина АВ, то АВ = 2х.
В: А чему будет равна сторона ВС?
О: ON половина ВС , значит ВС = 2(х + 6).
В: Все ли данные задачи мы использовали?
О: Да.
В: Достаточно ли нам их, чтобы составить уравнение?
О: Нет.
В: Какое данное можно добавить в условие задачи, чтобы она
имела решение?
Один из вариантов, который может быть предложен учащимися.
О: Пусть будет известен периметр. Р = 44 см.
В: Тогда какое уравнение мы получим?
О: 4х + 4( х + 6) = 44
ІІІ. Реализация плана решения
Решаем задачу с помощью добавленного данного.
Методика работы с задачей с избыточным условием будет следующей. Рассмотрим задачу: Точки А, В, С лежат на окружности с центром в точке О, ∠ АВС = 50°, ∪ АВ:∪ СВ = 5:8. Найти ∠ АОС.
I. Осмысление условия
В: Какая геометрическая фигура нам дана?
О: Окружность.
В: Что сказано о точках А, В, С?
О: Они принадлежат окружности.
В: Какие величины нам известны в задаче?
О: ∠ АВС=50°, ∪ АВ:∪ СВ = 5:8.
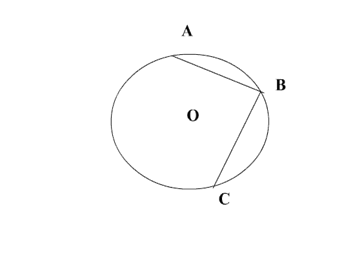
Запишем условие задачи:
Дано: (О, г) А,В,С Є (О, г)
∠ АВС= 50°,∪ АВ:∪ СВ=5:8
Найти: ∠ АОС
II. Поиск пути решения
В: Что нужно найти?
О: ∠ АОС
В: Каким углом является ∠ АВС?
О: Вписанным углом.
В: Каким углом является ∠ АОС?
О: Центральным углом.
В: Что общего у этих углов?
О: Они опираются на одну дугу.
В: Что можно сказать о ∪ АС если ∠ АВС=50°?
О: ∪ АС будет в два раза больше чем ∠ АВС.
В: Сможем ли мы найти ∠ АОС зная длину дуги на которую он опирается?
О: Да, он равен длине этой дуги.
В: Все ли данные задачи мы использовали?
О: Нет, еще есть отношение ∪ АВ:∪ СВ = 5:8.
В: Получим ли мы ответ, не используя это отношение?
О: Да.
В: Каким данным является ∪ АВ:∪ СВ = 5:8?
О: Лишним, в решении задачи мы его не используем.
Убедимся в этом, реализуя наш план решения.
III. Реализация плана решения
∠ АВС – вписанный, опирается на ∪ АС. Значит ∠ АВС=½ ∪ АС ⇒ ∪ АС= 2∠ АВС. ∪ АС = 100°.
∠ АОС – центральный, опирается на ∪ АС. Значит ∠ АОС= ∪ АС ⇒ ∠ АОС = 100°.
Убедились, что отношение ∪ АВ:∪ СВ = 5:8 являлось избыточным данным в задаче.
Возьмем задачу с противоречивым условием. Покажем методику поиска пути ее решения.
Вписать в окружность трапецию, углы которой находятся в следующем отношении 3:2:4:3.
I. Осмысление условия
В: Что нам дано?
О: Окружность и какая-то трапеция.
В: Что нам известно о этой трапеции?
О: Ее углы находятся в соотношении 3:2:4:3.
В: Можем ли мы сделать какие-нибудь выводы из соотношения углов трапеции?
О: Да.
В: Что можно сказать о трапеции?
О: Она равнобедренная.
В: Что является решением задачи?
О: Вписанная в окружность трапеция.
Запишем условие:
Дано: (О,r), ABCD – трапеция,
3:2:4:3 – отношение углов трапеции.
Вписать трапецию в окружность.
II. Поиск пути решения.
В: Что можем найти?
О: Углы трапеции.
В: Откуда мы их найдем?
О: Из соотношения 3:2:4:3.
В: Что удобнее обозначить за х?
О: Один из углов, т.к. она равнобедренная, то лучше два равных угла обозначить за х?
В: Чему равны другие углы?
О: х, 2/3х, 4/3х, х.
В: Какое уравнение можно составить?
О: Зная сумму углов четырехугольника, будет:
х + 2/3х + 4/3х + х = 360º
I. Реализация плана решения
Составим уравнение: х + 2/3х + 4/3х + х = 360º
Находим х= 90º, ∠ 1=∠ 4=90º
∠ 2= 60º, ∠ 3= 120º
Построим эту трапецию.
В: Попробуйте вписать ее в окружность?
О: Не получается.
В: Любую ли трапецию можно вписать в окружность?
О: Нет.
В: Какому условию должна удовлетворять трапеция, чтобы ее можно было вписать в окружность?
О: Сумма пар противоположных углов равна 180º.
В: Выполняется ли это условие в нашей задаче?
О: Нет, 90º + 120º ¹ 180° и 60°+ 90°¹180°.
В: Можем ли мы решить эту задачу?
О: Нет.
В: В чем заключается противоречие условия?
О: Отношение углов не соответствует требованию задачи.
При решении задач переопределённых, но имеющих в условии противоречие, ученики после небольшой тренировки находят очевидные или слабо скрытые противоречия, но, если противоречие хоть сколько-нибудь завуалировано, не замечают его и просто игнорируют, вместо того чтобы вернуться к условию задачи и проверить решение. Использование задач с противоречивыми данными позволит учащимся заметить (не без помощи учителя) полезность вдумчивого анализа условия, в результате которого можно выявить противоречивость и тем самым не искать решения, т. е. облегчить себе работу. А поскольку никогда не ясно, есть ли противоречие в условии задачи или нет, то вдумчивому анализу будут подвергаться условия всех задач, что следует считать чрезвычайно полезным качеством решателя задач.
На практике получается, что чаще всего процесс решения задач на уроке обладает некоторой рутинностью и оставляет ученику мало возможностей для творчества. Со временем такая специфика задач вырабатывает у ученика некоторый неправильный стереотип мышления, относящийся к решению задач. Ученик просто ищет стандартную ситуацию, к которой можно было бы применить известные формулы и теоремы, и теряется, когда предложенная задача требует даже несложного нестандартного подхода. Поэтому применение на уроках математики задач с аномальным условием заставляет учащихся включать все мыслительные и творческие способности, совершенствуя тем самым их знания и умения, и в результате – отлично усвоенный материал и развитые способности.
Рецензенты:
Усманов В.В., д.п.н., профессор, первый проректор, проректор по научной работе, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Данилов А. М., д.т.н., профессор, заведующий кафедрой «Математики и математического моделирования», ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Библиографическая ссылка
Акимова И.В., Буркина В.А., Титова Е.И. МОДЕЛИРОВАНИЕ ЗАДАЧ С АНОМАЛЬНЫМ УСЛОВИЕМ И МЕТОДИКА ПУТИ ПОИСКА ИХ РЕШЕНИЯ // Современные проблемы науки и образования. 2014. № 1. ;URL: https://science-education.ru/ru/article/view?id=12117 (дата обращения: 11.02.2026).



