Введение
Отечественные предприятия авиационного двигателестроения выпускают газотурбинные установки (ГТУ) для электроэнергетики. При этом примерно 70...75 % основных узлов и деталей базового авиационного двигателя удается сохранить. Газотурбинные электростанции (ГТЭС) на базе таких конвертированных авиационных ГТУ обладают целой совокупностью достоинств.
В то же время по-прежнему актуальны вопросы повышения качества вырабатываемой электроэнергии. Определенные проблемы во многом обусловлены физическими принципами работы двухвальных энергетических ГТУ. Отсутствие жесткой механической связи между валами компрессора и свободной турбины делает ГТУ сильно инерционным и затрудняет управление им. Это особенно сильно сказывается при резких изменениях режима. Например, отдельные заказчики отмечают, что мини-электростанция устойчиво выдерживает электрическую нагрузку, но весьма тяжело реагирует на значительные изменения нагрузки и переход от параллельной работы с сетью на изолированный режим работы. При этом имеют место частые аварийные остановки агрегатов, сопровождающиеся потерей питания собственных нужд. Это, как правило, влечет за собой повреждения наиболее нагруженных узлов (подшипников турбонагнетателей, клапанов и т.д.).
Таким образом, один из главных резервов совершенствования характеристик наземных газотурбинных установок (ГТУ) заключается в более полном использовании возможностей систем автоматического управления (САУ) [3].
Известно, что наиболее конструктивный путь решения задачи синтеза регуляторов – это использование методов нелинейного программирования [5], которые целесообразно использовать и при настройке регуляторов САУ. При этом показатели качества на каждом шаге направленного поиска могут определяться по результатам численного интегрирования дифференциальных уравнений, описывающих динамику системы [5].
Эти уравнения, как правило, представляют собой совместную модель ГТУ и нагрузки. Такая модель может быть получена двумя основными способами: или на основе описания физики процессов, или по результатам идентификации. В связи с использованием поисковых алгоритмов настройки существенно возрастают требования к быстродействию математической модели «ГТУ – нагрузка». Поэтому предпочтительной является упрощенная быстрорешаемая модель, получаемая с помощью идентификации по экспериментальным данным. В свою очередь модель на основе физики процессов может быть использована как поверочная при однократном воспроизведении переходного процесса.
Быстрорешаемые модели авиационных ГТУ широко используются при исследовании САУ ГТУ [2]. При рассмотрении ГТУ газотурбинных электростанций (ГТЭС) могут в дополнение к ним использоваться быстрорешаемые модели для всей электроэнергетической системы в целом [4].
Рассмотрим реализацию автоматической настройки САУ ГТУ при использовании быстрорешаемых моделей, полученных по экспериментальным данным. Алгоритм настройки реализован в составе программного комплекса (ПК) «ЭлектроДин» [7].
При этом решались следующие задачи: выбор критерия оптимизации; выбор методов оптимизации; программная реализация на языке Java в составе модуля автоматической настройки САУ ГТУ ПК «ЭлектроДин».
Критерий автоматической настройки системы управления
Как правило, принято считать идеальным переходным процессом или ступенчатый (скачкообразный) переходной процесс, протекающий мгновенно и без перерегулирования, или процесс, представляемый экспонентной с заданными параметрами. В практике проектирования систем управления наибольшее применение находят линейные и квадратичные интегральные критерии качества [1].
Рассмотрим в качестве критерия оптимизации интегральный критерий вида:
![]() ,
,
где e – отклонение регулируемого параметра от заданного значения, τ – постоянная, имеющая размерность времени [1].
Данный критерий минимизирует как отклонение регулируемого параметра, так и скорость изменения данного параметра, уменьшая колебательность. Таким образом, идеализированным переходным процессом в этом случае считается экспонента, к которой и должен стремиться реальный переходный процесс.
В простейшем случае оптимизация выполняется по выходной координате – частоте вращения свободной турбины. Хотя такая стратегия не всегда дает положительных результатов, поэтому, по крайней мере, необходимо брать еще входную координату – угол дозатора топлива. В противном случае входная переменная, а вместе с ней расход топлива и частота вращения турбокомпрессора могут иметь колебательный характер, несмотря на плавное изменение частоты вращения свободной турбины.
Учет нескольких переменных в общем критерии автоматической настройки САУ ГТУ может осуществляться посредством сложения критериев для каждой переменной в отдельности с весовыми коэффициентами.
Методы оптимизации
Поскольку ПК «ЭлектроДин» написан на языке программирования Java, наиболее просто использовать готовые библиотеки алгоритмов оптимизации, например, библиотеку ApacheCommonsMath [6], распространяемую бесплатно по лицензии Apache. Библиотека ApacheCommonsMath – легковесная библиотека из математических и статистических компонентов. Она имеет в своем составе методы оптимизации: Гаусса – Ньютона; Левенберга – Марквардта; сопряженных градиентов; Брента. А также пакет алгоритмов оптимизации, которые не требуют расчета производных:
- метод Нелдера – Мида;
- метод Пауэлла;
- метод BOBYQA;
- метод CMA-ES.
Указанные методы представляют интерес для решаемой задачи.
Метод Нелдера – Мида, также известный как метод деформируемого многогранника и симплекс-метод, – метод безусловной оптимизации функции от нескольких переменных, не использующий производной (точнее – градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям. Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.
Метод Пауэлла основан на последовательном применении процедуры оценивания с использованием квадратичной аппроксимации.
BOBYQA (BoundOptimizationByQuadraticApproximation) – это итеративный алгоритм Пауэлла нахождения минимума функции с учетом нижней и верхней границпеременных.
Метод CMA-ES (CovarianceMatrixAdaptationEvolutionStrategy) – метод эволюционной стратегии с адаптацией матрицы ковариаций. Алгоритм для сложных нелинейных невыпуклых задач оптимизации в непрерывной области.
Первые три алгоритма находят локальный минимум и могут остановиться в нем, а метод CMA-ES является методом поиска глобального минимума.
Причем рекомендуется совместное поочередное использование нескольких алгоритмов оптимизации, что повышает эффективность и качество настройки САУ. Структурная схема рекомендуемого алгоритма настройки САУ с использованием указанных методов представлена на рисунке 1.
Метод Нелдера – Мида дает наихудшие результаты в сравнении с остальными, иногда равняясь на методы BOBYQA и Powell, поэтому его использование неэффективно.
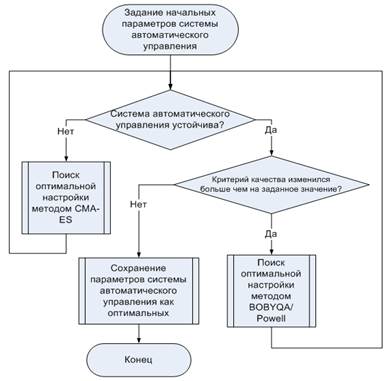
Рисунок 1. Структурная схема алгоритма поиска оптимальной настройки САУ
Программная реализация
Методы оптимизации, не требующие расчета производной в ApacheCommonsMath, реализованы в пакете org.apache.commons.math3.optimization.direct. И имеют соответствующее название классов: PowellOptimizer; BOBYQAOptimizer; CMAESOptimizer. Метод Нелдера – Мида реализуется посредством экземпляра класса SimplexOptimizer и установкой в его метод setSimplex объекта класса NelderMeadSimplex. Запуск оптимизации осуществляется вызовом метода optimize. Ниже представлен программный код запуска метода оптимизации Нелдера – Мида.
CMAESOptimizer optimizer = new CMAESOptimizer();
PointValuePairresultValues = optimizer.optimize(maxEvaluations, functionCalculator, GoalType.MINIMIZE, initialValues);
Где initialValues – начальные значения параметров САУГТУ (для нашей задачи); result Values – оптимальные значения параметров САУ; maxEvaluations –максимальное количество расчетов функции; functionCalculator – объект, реализующий интерфейс MultivariateFunctionс методом value для расчета значения функции. В данном методе реализуется моделирование ГТУ совместно с САУ и моделью нагрузки, а затем по полученным графикам угла дозатора топлива и частоты вращения свободной турбины расчет интегрального критерия, представленного выше. Структурная схема расчета функции представлена на рисунке 2.
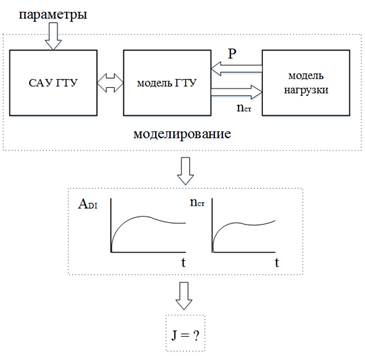
Рисунок 2. Структурная схема содержимого расчета функции
На рисунке 2 буквой P обозначена активная мощность нагрузки, nСТ – частота вращения свободной турбины, ADI – угол дозатора топлива.
Для создания универсального модуля автоматической настройки САУ ГТУ, работающего для различных моделей ГТУ, САУ ГТУ и нагрузки, необходимо воспользоваться полиморфизмом. Для этого на целевом языке Java необходимо объявление интерфейсов ISauGtu, IGtu, IGtuLoad соответственно. Помимо этого интерфейсы необходимы как минимум еще для следующих компонентов: IOptimizer – для метода оптимизации; IFunctionCalculator – для калькулятора функции (для интеграции различных библиотек оптимизации); IOptimizeCriterion – для критерия оптимизации. Как известно, интерфейс необходим, чтобы иметь различную их реализацию. Поэтому отдельные модули программы должны взаимодействовать друг с другом через интерфейсы.
Поскольку не все из методов оптимизации учитывают ограничения параметров, то их учет можно перенести в калькулятор функции. При выходе параметра за заданные границы, необходимо возвращать значение функции равным бесконечности. Если смоделированный переходный процесс получился неустойчивым, также следует возвращать значение функции равным бесконечности.
Методы оптимизации библиотеки ApacheCommonsMath были интегрированы в состав ранее разработанного модуля автоматической настройки САУ ГТУ ПК «ЭлектроДин» (рисунок 3).
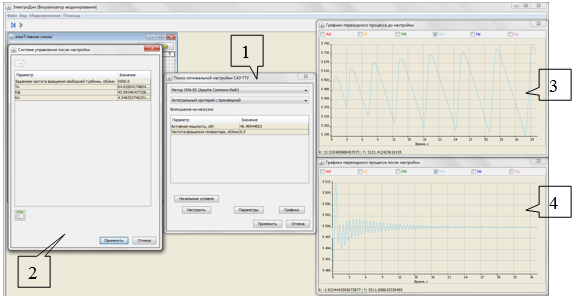
Рисунок 3. Модуль настройки САУ ГТУ программного комплекса «ЭлектроДин»: 1 – главное окно модуля настройки САУ ГТУ, 2 – окно отображения настроенных параметров САУ, 3 – окно отображения результатов моделирования до настройки, 4 – окно отображения результатов моделирования после настройки
Результаты
На рисунке 4 представлен результат настройки модели САУ ГТУ описанными выше методами. В качестве модели ГТУ используется быстрорешаемая модель газотурбинного двигателя Д30. Используемая модель САУ ГТУ представлена в [8]. Для имитации наброса нагрузки применяется быстрорешаемая модель электроэнергетической системы (синхронный генератор и активно-индуктивная нагрузка), реализованная в пространстве состояний.
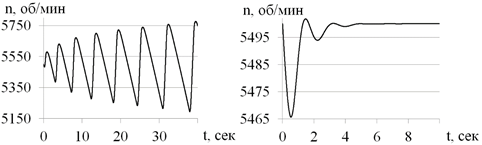
Рисунок 4. Графики частоты вращения свободной турбины (n) до (слева) и после (справа) настройки
На рисунке 4 слева изображен график частоты вращения свободной турбины до настройки, а справа график данного параметра после настройки методами CMA-ES и Powell поочередно.
Заключение
Использование методов библиотеки ApacheCommonsMath для предварительной автоматической настройки САУ на компьютерной быстрорешаемой модели ГТУ способно существенно расширить функциональность модуля настройки ПК «ЭлектроДин» и, как следствие, сократить время испытаний, а также повысить качество настройки за счет проведения многократных компьютерных экспериментов для открытого множества характерных режимов.
Рецензенты:
Бочкарёв С.В., д.т.н., доцент кафедры МСА, ПНИПУ, г. Пермь.
Цаплин А.И., д.т.н., зав. кафедрой общей физики, ПНИПУ, г. Пермь.
Библиографическая ссылка
Кавалеров Б.В., Один К.А., Даденков Д.А. АВТОМАТИЧЕСКАЯ НАСТРОЙКА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ГАЗОТУРБИННЫМИ УСТАНОВКАМИ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМОВ БИБЛИОТЕКИ APACHE COMMONS MATH // Современные проблемы науки и образования. 2014. № 1. ;URL: https://science-education.ru/ru/article/view?id=12039 (дата обращения: 08.02.2026).



