Наглядное моделирование в процессе обучения математике студентов технического профиля при формировании исследовательской деятельности выступает методологической основой содержания математического знания.
Наглядность первоначально в дидактике рассматривалась как принцип обучения, согласно которому обучение строится на конкретных образах, непосредственно воспроизводимых обучающимися. В связи с созданием теории обучения разрабатывались средства наглядности (объект или явление, образ, модель, схема). В результате систематизации методов обучения в дидактике сформировался объяснительно-иллюстративный метод обучения, где наглядные и словесные приёмы обучения применялись одновременно. С развитием дидактики и её связей с возрастной и педагогической психологией обучение от ассоциативных теорий осознанного запоминания перешло к развивающим теориям обучения, основанным на деятельностном подходе. В связи с этим необходимо переосмысление и обновление методической системы обучения математике и её компонентов: целей, содержания, способов, форм и средств интеграции, а также формирование опыта личности студента в математическом исследовании. Для глубокого и осознанного усвоения математических знаний метод наглядного моделирования в обучении выступает связующим звеном в ряду других методов обучения: проблемным, проектным, исследовательским, абстрактно-дедуктивным и индуктивным методами познания. В обучении математике наглядное моделирование занимает особое место. Многие математические теории обладают высокой степенью абстракции, что обуславливает представление информации в знаково-символьной форме. Наглядное моделирование как приём обучения присутствует во всех методах объяснения, как компонент понимания и образного представления математических знаний. Это и объясняет его выбор интегрирующим фактором в обучении математике, направленного на формирование и развитие исследовательской деятельности студентов технических вузов в процессе обучения математике. Подтверждением актуальности и целесообразности применения метода наглядного моделирования является создание математиками XVII–XVIII веков e-d языка для обоснования предельных процессов. «Такое наглядное моделирование создавало возможность, в том числе, встать на новый, социально-значимый уровень понимания и объяснения сущности основ дифференциального и интегрального исчисления» [5].
В исследованиях Н.Г. Салминой выделены виды наглядного моделирования, на основе способа ведущей деятельности: моделирование, кодирование, схематизация, замещение [4].
Построение процесса обучения будущих инженеров, направленного на формирование исследовательской деятельности студентов, осуществлялось нами на основе разработанной Е.И. Смирновым и его учениками концепции наглядно-модельного обучения. Предпочтение отдается «наглядной» модели как опоре на устойчивые ассоциации, простые геометрические формы, психологические законы восприятия и нейрофизиологические механизмы памяти.
Модель должна отражать суть понятия, формы и методы исследования. Наглядно-модельное обучение включает следующие компоненты:
- выделение базовых учебных элементов (понятия, теоремы, задачи);
- создание модели идеального объекта (схемы, графики, образец решения задачи);
- взаимный переход знаковых систем к знаково-символическим подсистемам;
- вербальный переход от конкретно-деятельностных аспектов к обобщенным знаковым формам.
Содержательной основой интеграции фундаментальных и прикладных математических знаний студентов технического профиля является знаково-символьная наглядность. Видом знакового моделирования выделено математическое моделирование, при котором исследование объекта осуществляется посредством модели, сформулированной на языке математики и с использованием тех или иных математических методов. Очевидно, что для будущих инженеров особый интерес представляют примеры технических математических моделей. Покажем реализацию механизмов наглядного моделирования в процессе обучения математике на примере преподавания курса: «Математическое моделирование и обыкновенные дифференциальные уравнения». Данный курс направлен на формирование у бакалавров и магистров общих представлений о теоретико-методологических основах научно-исследовательской деятельности, формирование методологической и научной культуры.
Цель курса:
- сформировать у студентов целостное представление о роли математических методов и математических моделей в профессиональной деятельности студентов инженерных факультетов;
- раскрыть основные понятия и методы математического моделирования инженерных процессов;
- развить у студентов навыки применения методологии и методов математического моделирования с использованием математического аппарата, а также вычислительной техники к прикладным инженерным задачам;
- научить студентов самостоятельной работе с учебной и научной литературой;
- развивать и совершенствовать логическое и аналитическое мышление для умения анализировать, сравнивать, оценивать, выбирать, интерпретировать и т.д.
Следует также отметить возрастающую роль различных математических методов (появление которых связано не только с внедрением компьютерной техники) в преподавании почти всех гуманитарных, медицинских, философских и ряда с других дисциплин, а также с философским осмыслением роли и необходимости математических методов в различных сферах человеческой деятельности. В работе показана применимость и эффективность метода аналогии, как методологического и математического метода изложения и изучения некоторых классов нелинейных конкретных физических и биологических модельных задач при соответствующем обосновании. Этот достаточно конструктивный и эффективной метод, удобный для его изложения и усвоения слушателями от бакалавра, магистра и до аспиранта, пока мало используется преподавателями математики в высшей школе. Его совместное применение в сочетании с некоторыми математическими методами, в частности, с достаточно новым математическим методом, методом унитарных преобразований (не требующих громоздких преобразований и вычислений), позволяет исследовать вопросы устойчивости большого класса модельных нелинейных систем ОДУ (не претендуя на универсальность), описывающих некоторые физические, биологические процессы, при их квазилинейной матричной записи. Метод аналогии в данном случае предполагает:
Сведение исследуемых нелинейных модельных уравнений, описывающих различные физические, социальные, биологические и некоторые другие исследуемые процессы к матричной форме записи.
Анализ полученных (в некотором смысле аналогичных) нелинейных систем ОДУ и изучение характера существующих изолированных точек покоя. Выявление внутреннего (математически обоснованного) сходства различных нелинейных систем ОДУ, возникающих при описании различных изучаемых процессов, что позволит применить метод внутренний аналогии.
Для простейших моделей в некритических случаях для анализа найденных точек покоя можно применить теорему Ляпунова об асимптотический устойчивости по первому приближению (то есть, здесь применим метод «прямой аналогии»).
В критических случаях (когда спектр матрицы изучаемой линеаризованной системы в данной точке покоя является чисто мнимым) может быть использован более сложный классический метод функций Ляпунова, для построения которых в общем случае пока нет достаточно конструктивного алгоритма.
Наличие аналогии при изучении полученных нелинейных модельных систем позволяет в некоторых случаях (особенно при анализе критических точек покоя) применить достаточно новый (но весьма эффективный) метод унитарных преобразований.
Наличие внутренней аналогии (внутреннего обоснованного сходства) для сравнительного анализа при исследовании квазилинейной систем вида:
ż =A(z)z (1)
с нелинейной нормальной матрицей A(z) позволило применить метод аналогий и спектральный вариант метода унитарных преобразований в данной работе в следующих случаях:
а) в тех случаях, когда нелинейная матрица A(z) исходной системы ОДУ является нормальной (т.е. имеет место, тождественное равенство:
A(z)A·(z) ≡ A·(z)A(z) в некоторой области ),
;
б) либо, в случае, когда в областиWсуществует специальная диагональная матрица Q(z) такая, что матрицаB(z)=Q(z)A(z) является нормальной;
в) либо, в другой ситуации, когда матрица A(z) исходной системы является области W суммой нормальных матриц, то есть в случае, когда для системы 
=A(z)z матрица A(z) представима виде A(z) суммы нормальных матриц B(z) и T(z).
Эффективность и конструктивность разработанного подхода продемонстрируем при исследовании конкретных линейных и нелинейных нетривиальных примеров.
При изложении различных разделов теории дифференциальных уравнений (особенно на инженерных факультетах) всегда возникает проблема выбора наиболее оптимальной и эффективной методики изложения данного материала. За последние 100 лет (а может и более) не было предложено ни одного достаточно конструктивного аналитического метода исследования и метода изложения данного материала. Все большее внимание уделяется различным численным алгоритмам исследования указанных задач. Лишь через 50 лет после реального введения в научную практику векторно-матричного способа записи системы дифференциальных уравнений в 90-е годы 20-го века в работах Коняева Ю.А. был разработан (не претендуя на универсальность) ряд новых конструктивных аналитических методов исследования в качественной теории дифференциальных уравнений, включая вопросы устойчивости, а также в теории регулярных возмущений [1].
При изложении курса были исследованы и реализованы в качестве методов анализа и преподавания (совместно с методом обоснованной аналогии) два новых алгоритма (метод унитарных преобразований и метод расщепления) [2]. Это позволило на их базе создать новые эффективные методики изложения соответствующих разделов математики, что нашло подтверждение при их преподавании на инженерном факультете.
Сущность метода унитарных преобразований при анализе квазилинейных систем вида 
с нормальной матрицей
состоит в исследовании устойчивости их решения с учётом структуры её спектра и свойств нормальных матриц (приводимости нормальных матриц к диагональному виду с помощью унитарных преобразований), что для произвольных систем в общем случае не имеет места.
Это позволило доказать ряд нетривиальных теорем (и изучить соответствующие примеры), что можно считать обобщением классической теоремы Ляпунова об асимптотической устойчивости по первому приближению на указанный класс задач [3].
Сущность метода расщепления состоит в новом эффективном алгоритме нахождения спектра
и собственных векторов 
возмущенной матрицы 
т.е. решения спектральной задачи:
после её записи в матричной форме
, где (при наличии простого спектра)
} и 
(при дальнейшем использовании аппарата метода расщепления [69]), что выгодно отличается от классических методов [64].
Покажем полезность данных методов при исследовании реальной инженерно- физической задачи в теории гироскопов, а именно – при анализе модельной системы уравнений, описывающей процесс колебания тонкого кольцевого резонатора волнового твердотельного гироскопа (ВТГ) с системой поддерживающих торсионов, который без учёта демпфирования сводится к исследованию системы ОДУ четвертого порядка вида:
(2)
где компоненты вектора 
медленно изменяющиеся переменные, связанные с формой колебаний, матрицаB(z),
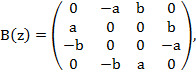
где её компоненты a и b равны соответственно:
x – параметр, характеризующий нелинейную упругость материала резонатора;
безразмерная угловая скорость основания гироскопа;
и
– функции, представляющие собой первые интегралы исходной системы.
Так как матрица B(z) является нормальной и кососимметрической, и с учётом силу этого имеет чисто мнимый спектр, то процесс колебаний, определяемой системой (2), всегда будет устойчивым в силу ранее доказанных теорем.
Для определения более детальной структуры колебаний, определяемой модельной системой (2), следует найти её спектр, что в данном случае является нетривиальной задачей.
Для упрощения дальнейшего анализа представим матрицу B(z) в виде суммы двух нормальных и кососимметрических матриц
B(z)=F(z) + G(z)
где матрицы, равные:
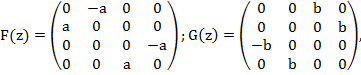
также имеют чисто мнимый спектр
,
что позволяет сделать вывод о том, что структура решения системы (2) будет иметь колебательный характер вида:
,
где значения постоянных векторов 
будут определяться начальными условиями.
Метод аналогии в сочетании с новым вариантом метода расщепления позволил также изучить целый класс спектральных статических и динамических задач, связанных, в частности, с исследованием модельного уравнения колебаний волнового твердотельного гироскопа (ВТГ).
Только тогда, когда усвоенная информация и приобретенные способы деятельности становятся не только предметом познания, но и инструментом для самостоятельного приобретения нового знания, можно говорить о развивающем характере познавательной деятельности.
Рецензенты:
Санина Е.И., д.п.н., профессор кафедры психологии и педагогики Российского университета дружбы народов, г. Москва.
Коняев Ю.А., д.ф.-м.н., профессор кафедры высшей математики Российского университета дружбы народов, г. Москва.
Библиографическая ссылка
Вакджира М.Б. НАГЛЯДНОЕ МОДЕЛИРОВАНИЕ КАК ОСНОВА ФОРМИРОВАНИЯ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ СТУДЕНТОВ ТЕХНИЧЕСКИХ ВУЗОВ В ПРОЦЕССЕ ОБУЧЕНИЯ МАТЕМАТИКЕ // Современные проблемы науки и образования. – 2014. – № 1. ;URL: https://science-education.ru/ru/article/view?id=11954 (дата обращения: 21.11.2024).