Деятельность современного экономиста любой области требует умения анализировать имеющую информацию и моделировать описываемое экономическое явление или процесс [5], решать типовые математические задачи, используемые при принятии управленческих решений с применением информационных технологий. Успешное решение поставленных задач невозможно как без навыков применения современного математического инструментария, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений и процессов, так и без владения программным обеспечением для работы с деловой информацией. В исследованиях современной экономики применяются различные оптимизационные методы, опирающиеся на математическое программирование, сетевое планирование, теорию массового обслуживания и т.д., а также на теорию игр.
Теория игр – математическая схема анализа стратегического взаимодействия конкурирующих сторон. Она позволяет объяснить логику рационального поведения в условиях конфликта интересов. Появление теории игр принято связывать с публикацией в 1944 г. монографии Джона фон Неймана и Оскара Моргенштерна «Теория игр и экономическое поведение».
Поскольку игры берут свое начало в конфликте интересов, оптимальным решением игры является одна или несколько стратегий каждого из игроков, при этом любое отклонение от данных стратегий не улучшает плату тому или другому игроку. Эти решения могут быть в виде единственной чистой стратегии или нескольких стратегий, которые являются смешанными в соответствии с заданными вероятностями.
В статье приводится решение типичного примера, относящегося к рекламированию конкурирующих товаров, с применением табличного процессора Microsoft Excel.
Две компании продают два вида лекарств против гриппа. Компания А рекламирует продукцию на радио (А1), телевидении (А2) и в газетах (А3). Компания В, в дополнение к использованию радио (В1), телевидения (В2) и газет (В3), рассылает также по почте брошюры (В4). В зависимости от умения и интенсивности проведения рекламной кампании каждая из компаний может привлечь на свою сторону часть клиентов конкурирующей компании. Приведенная ниже матрица (табл. 1) характеризует процент клиентов, привлеченных или потерянных компанией А.
Таблица 1. Матрица процентов клиентов, привлеченных или потерянных компанией А
|
|
В1 |
В2 |
В3 |
В4 |
|
А1 |
8 |
-2 |
9 |
-3 |
|
А2 |
6 |
4 |
6 |
8 |
|
А3 |
-2 |
10 |
-9 |
6 |
Нахождение смешанных стратегий двух компаний может быть сведено к решению пары двойственных задач линейного программирования, для составления которых исходная матрица должна быть скорректирована (табл. 2) с целью присутствия в ней только положительных элементов.
Таблица 2. Скорректированная матрица процентов клиентов, привлеченных или потерянных компанией А
|
|
В1 |
В2 |
В3 |
В4 |
|
А1 |
18 |
8 |
19 |
7 |
|
А2 |
16 |
14 |
16 |
18 |
|
А3 |
8 |
20 |
1 |
16 |
В соответствии с данными скорректированной матрицы процентов клиентов, привлеченных или потерянных компанией А, задача линейного программирования для определения смешанной стратегии компании А будет иметь вид
.
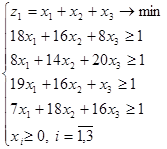Цена игры с позиции компании А будет определяться как 
, а скорректированная цена - 
.
- смешанная стратегия компании А.
Задача линейного программирования для определения смешанной стратегии компании В будет иметь вид
.
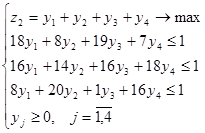Цена игры с позиции компании В будет определяться как 
, а скорректированная цена - 
.
- смешанная стратегия компании В.
Исходные данные и связи между ними в виде формул для нахождения оптимальной стратегии компании В представлены на рис. 1. Диалоговое окно Поиск решения с указанием целевой функции, изменяемых ячеек и ограничений соответствует рис. 2. Результаты работы надстройки Microsoft Excel, а также цена игры с позиции компании В, скорректированная цена игры, а также смешанная стратегия данной компании указаны на рис. 3.
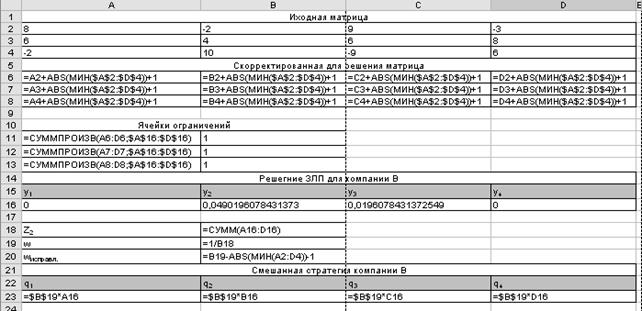
Рис. 1. Исходные данные и связи между ними в виде формул для компании В
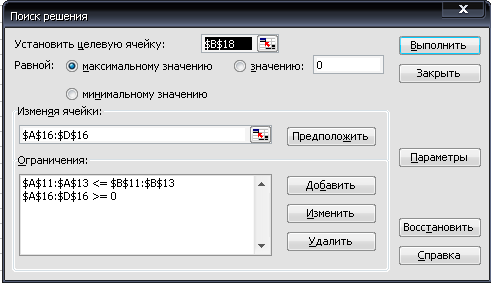
Рис. 2. Диалоговое окно Поиск решения для компании В
Исходные данные и связи между ними в виде формул для нахождения оптимальной стратегии компании А представлены на рис. 4. Результаты работы надстройки Microsoft Excel, а также цена игры с позиции компании А, скорректированная цена игры, а также смешанная стратегия данной компании указаны на рис. 5.
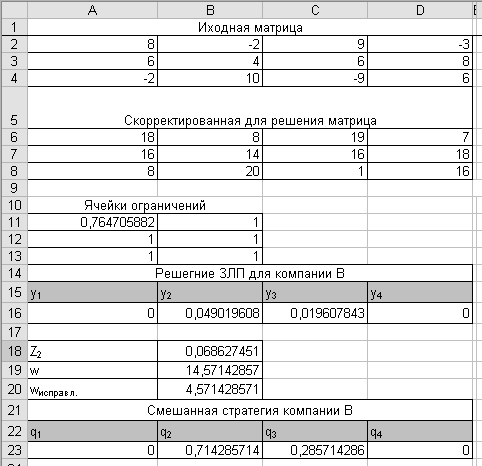
Рис. 3. Результаты решения для компании В
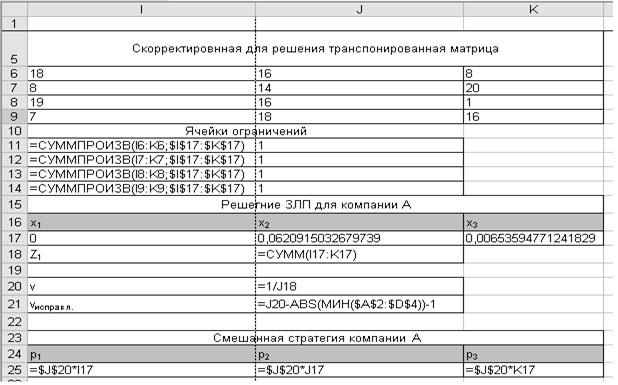
Рис. 4. Исходные данные и связи между ними в виде формул для компании А
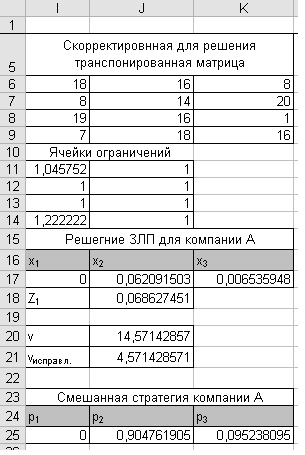
Рис. 5. Результаты решения для компании А
Анализ полученных результатов позволяет сделать вывод том, что решение в виде чистой стратегии неприемлемо. Обеим компаниям следует проводить рекламную кампанию на телевидении и в газетах. При этом выигрыш будет в пользу компании А, так как ее рынок увеличится на 4,57%. Любое отклонение от стратегии, полученной для компании В, не приведет при этом к улучшению ситуации, так как рекламная кампания на телевидении и в газетах с вероятностями р2.=0,905 и р3=0,095 для компании А и q2.=0,714 и q3=0,286 для компании В соответствует седловой точке.
Рецензенты:
Ахполова В.Б., д.э.н, доцент, доцент кафедры менеджмента ГБОУ ВПО «Северо-Осетинский государственный педагогический институт», г. Владикавказ.
Дзагоева М.Р., д.э.н, профессор кафедры «Налоги и налогообложение» Северо-Осетинского государственного университета им. К.Л. Хетагурова, г. Владикавказ.
Макринова Е.И., д.э.н., профессор, заведующая кафедрой сервиса и туризма Белгородского университета кооперации экономики и права, г. Белгород.
Библиографическая ссылка
Цахоева А.Ф. РЕШЕНИЕ ЗАДАЧИ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ КОНФЛИКТНОЙ СИТУАЦИИ С ПРИМЕНЕНИЕМ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ // Современные проблемы науки и образования. – 2014. – № 1. ;URL: https://science-education.ru/ru/article/view?id=11926 (дата обращения: 21.11.2024).