Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бабенко В.Н. 1

---

1 ФГБОУ ВПО "Кубанский государственный университет"

В работе [3] был изложен алгоритм Качмажа для решения систем линейных алгебраических уравнений большой размерности, соответственно, в [2] для него проведено исследование скорости сходимости. Однако вопросы технологии вычислений, которые в современных условиях выходят на первый план, остались не раскрытыми. Данная статья призвана устранить образовавшийся пробел. В формуле для вычисления последовательности приближений, сходящейся к точному решению, используется псевдоинверсия матриц. Процедура ее вычисления ведет к неоправданно большим расходам машинных ресурсов. В представленной работе изложены теоретические обоснования, позволяющие избежать указанной процедуры. Затем подробно излагается технология вычислений последовательности приближений к точному решению. Аналогичные действия проведены в отношении алгоритма вычисления наклонов линейных многообразий. В статье указаны способ размещения векторов отражений и возможности эффективного обмена данными между оперативной и внешней памятью.

Статья в формате PDF

128 KB

преобразования отражения.

обмен данными между оперативной и внешней памятью

технология вычислений

система линейных уравнений большой размерности

псевдообращение матрицы

алгоритм

1. Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание. – М.: Мир, 1977. – 234 с.

2. Бабенко В.Н. Сходимость проекционного алгоритма Качмажа // Вычисл. матем. и матем. физики. – 1984. - №10. – C. 1571-1573.

3. Васильченко Г.П., Светлаков А.А. Проекционный алгоритм решения систем линейных алгебраических уравнений большой размерности // Вычисл. матем. и матем. физики. – 1980. - №1. – С. 3-10.

4. Годунов С.К. Решение систем линейных уравнений. – Новосибирск: Наука, 1980. – 177 с.

5. Годунов С.К., Антонов А.Г., Кирилюк О.П., Костин В.И. Гарантированная точность решения систем линейных уравнений в евклидовых пространствах. – Новосибирск: Наука, 1988. – 449 с.

6. Стренг Г. Линейная алгебра и ее применение. – М.: Мир, 1980. – 454 с.

Введение

Для решения систем линейных алгебраических уравнений большой размерности в [3] был предложен алгоритм (в дальнейшем мы будем называть его алгоритмом Качмажа, так как он является обобщением алгоритма указанного автора). Суть предложенного алгоритма заключается в следующем.

Пусть задана система линейных алгебраических уравнений

(1) ,

где х, у – суть N-мерные векторы, А – невырожденная матрица. Последовательность приближений , вычисляемых по формуле

(2),

, , сходится по евклидовой норме к – точному решению системы (1) [3]. Здесь матрица А и вектор у представляются следующим образом:

.

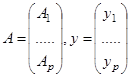В [2] был исследован характер сходимости вычислительного процесса (1). В частности, показано, что скорость сходимости метода Качмажа существенно зависит от наклонов между линейными многообразиями, определяемыми строками матриц .

Введем обозначения . Далее вычитая из обеих частей (2) вектор , получим

.

Норма разности двух смежных приближений , отнесенная к норме погрешности i-го приближения , тем больше, чем больше – наклон между линейными многообразиями , то есть справедливо неравенство

.

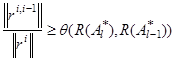Здесь – образы линейных операторов соответственно.

Тем самым показано, что повышение скорости сходимости метода Качмажа может быть достигнуто путем группирования подсистем линейных алгебраических уравнений.

Также были решены задачи выбора значения параметра останова вычислительного процесса и установления связанной с ним оценкой точности полученного приближенного решения. Процесс вычислений по формуле (2) следует продолжать до тех пор, пока приближенное решение не будет удовлетворять условию

(3) .

Но точное решение неизвестно, поэтому обычно используется другой критерий останова вычислений – выполнение неравенства

.

Пусть k и таковы, что

, тогда если для некоторого i выполняется неравенство

,

то процесс вычислений следует прекратить и в качестве принять . При этом будет обеспечено выполнение неравенства (3).

Поскольку скорость сходимости метода Качмажа существенно зависит от наклонов между линейными многообразиями, в [2] предложен алгоритм их вычисления:

1) k=1, взять произвольный вектор такой, что;

2) ;

3) ;

4) если , то перейти на 5), иначе k=k+1, и идти на 2);

5) ;

6) ;

7) конец.

Здесь через и обозначены ортопроекторы на соответственно. Как известно, [1, 6].

Достоинством алгоритма является его универсальность: метод Качмажа не опирается ни на какие частные свойства матрицы системы (1), за исключением требования невырожденности ее матрицы. Однако алгоритм не приобрел популярности, видимо, по той причине, что в формулах присутствует псевдообратная матрица , вычисление которой весьма накладно. В этой статье мы преследуем цель – предложить технологию вычислений в методе Качмажа, такую, что для ее реализации достаточно воспользоваться стандартными подпрограммами, имеющимися в большинстве пакетов программ вычислительной линейной алгебры, при этом вычисление псевдообратных матриц не требуется.

1. Технологические аспекты вычислений в методе Качмажа

В настоящее время вопросы разработки технологий вычислений в связи с их актуальностью вышли на первый план. Обратимся и мы к вопросу технологии вычислений метода Качмажа. Очевидно, непосредственное вычислений последовательности приближенных решений по формуле (2) неприемлемо, так как в ее состав входит псевдообратная матрица , вычисление которой является трудоемкой вычислительной задачей. Нетрудно показать, что можно избежать процедуры вычисления . Пусть матрица состоит из n строк и пусть и – произведения отражений, приводящие матрицу к двухдиагональному виду с нижней побочной диагональю. Другими словами,

,

где .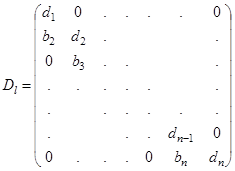

Легко обнаружить, что псевдорешение системы уравнений , задаваемое соотношением , где 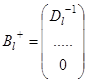, может быть определено по формулам:

(12);

. С учетом последних соотношений обратимся к формуле (2)

.

Введем обозначения: , , . С учетом этих обозначений мы можем записать

(13).

Определим структуру матрицы . Очевидно, и, следовательно, . Учитывая последние соотношения, (13) перепишем в виде

, где , а компоненты вектора определяются по формулам (12). Учитывая структуру векторов и , окончательно запишем

, где .

Подводя итоги нашим усилиям, изложим метод Качмажа в новом виде:

1) i=1, – произвольный вектор;

2) по матрице построить отражения и , приводящие матрицу к двухдиагональному виду и вычислить элементы матрицы ;

3) вычислить , , , где и ;

4) вычислить , где ;

5) если , то i=i+1 и идти на 2);

6) конец.

Аналогичные действия проведем в отношении алгоритма вычисления наклонов линейных многообразий. Введем обозначения: , – количество строк у матриц , соответственно. Пусть . Обращаясь к п. 2) алгоритма вычисления наклонов линейных многообразий, мы можем записать цепочку равенств

.

Структура матрицы нам известна, поэтому, введя обозначение , мы можем записать

, где .

Аналогично, обращаясь к пункту 3) алгоритма, запишем

.

Введя обозначение , мы получим формулу

, где .

В соответствии с изложенным выше, мы изменим алгоритм вычисления наклонов линейных многообразий.

1) k=1, взять произвольный вектор такой, что ;

2) , ,

где ;

3) , ,

где ;

4) если , то перейти на 5), иначе k=k+1, и идти на 2);

5) ;

6) ;

7) конец.

2. Обсуждение результатов

Анализируя изложенные алгоритмы, мы видим, что для их реализации достаточно воспользоваться стандартными вычислительными процедурами: приведения матрицы к двухдиагональному виду вычисления отраженного вектора, сложения векторов, вычисления скалярного произведения векторов и нормы вектора, имеющимися в большинстве пакетов программ по вычислительной линейной алгебре [4, 5]. Разрабатывать новые программы не нужно.

К достоинствам алгоритма Качмажа мы должны отнести простоту организации обмена данными между оперативной и внешней памятью (построчный обмен), кроме этого указанный обмен можно (должно) производить параллельно.

При выполнении i-той итерации векторы отражений и (), определяющие преобразованияотражения и , которые приводят матрицу к двухдиагональному виду , следует располагать в оперативной памяти (ОП) на месте, занимаемом исходной матрицей , а после итерации завершения данные, содержащие информацию о векторах отражения, — перенести во внешнюю память (ВП). Вычисленные элементы двух диагоналей матрицы ввиду незначительности занимаемого ими объема следует хранить в ОП. Когда , информацию о векторах отражения и можно получить построчным чтением массива ВП, ранее содержащим элементы матрицы .

Замечание 1. Обратимся к геометрической интерпретации метода Качмажа. С последовательностью приближений , где , свяжем последовательность точек . Нетрудно обнаружить, что для любого i точка является проекцией точки на гиперплоскость , поэтому метод Качмажа еще называют проекционным [3].

Рецензенты:

Лебедев К.А., д.ф.-м.н., профессор кафедры вычислительной математики и информатики ФГБОУ ВПО Кубанского государственного университета, г. Краснодар.

Усатиков С.В., д.ф.-м.н., профессор кафедры общей математики ФГБОУ ВПО Кубанского государственного технологического университета, г. Краснодар.

Библиографическая ссылка