Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Горшков Ю.Е. 1

---

1 ФГБОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова»

Проведен анализ методов условной минимизации и методов прямого поиска, применительно к решению задачи оптимизации параметров дугогасительной камеры. Для методов условной минимизации выявлено, что возможно применение методов штрафных и барьерных функций совместно с методами наискорейшего спуска или методом сопряженных направлений. Для методов прямого поиска выявлено, что в задаче минимизации энерговыделения в дугогасительной камере применение сеточного метода и его модификаций может оказаться эффективным при увеличении пробных шагов по параметрам оптимизации. Также при рассмотрении комплексного метода было отмечено, что его использование может существенно уменьшить время достижения минимума энерговыделения в камере. При практической реализации на ЭВМ рассматриваемых методов оптимизации были выявлены их недостатки. Наиболее подходящими для решения указанной выше задачи являются методы штрафной и барьерной функций, комплексный метод Бокса, метод скользящего допуска и случайный поиск с самообучением. При проведении ряда вычислительных экспериментов на ЭВМ было обнаружено, что комплексный метод Бокса показал наиболее быструю сходимость к решению задачи оптимизации параметров дугогасительной камеры автоматических выключателей.

Статья в формате PDF

143 KB

метод оптимизации

автоматический выключатель

дугогасительная камера

1. Антонов А.И. Переходный процесс в двумерной экстремальной системе при наличии запрещенных областей и случайном методе поиска // Задачи статистической оптимизации. Рига: Зинтане, 1971. С. 69-81.

2. Медведев Г.А., Рыжаков А.П. О применении алгоритмов случайного поиска в системах автоматической оптимизации // Задачи статистической оптимизации. Рига: Зинтане, 1971. С. 81-92.

3. Растригин Л.А., Рипа К.К. Автоматная теория случайного поиска. Рига: 3интане, 1973. 342 с.

4. Таев И.С., Егоров Е.Г., Горшков Ю.Е., Попова Е.П. Оптимизация параметров дугогасительной камеры электрического аппарата. М.: Эл. техн. пром., сер. «Аппараты низкого напряжения», 1981. 1(92).

5. Численные методы условной оптимизации / Под ред. А.А. Петрова. М.: Мир, 1977. 290 с.

6. Box M.J. A new method of constrained optimization and а compare sоn with other methods. Computer, 1965, №8, рp. 42-52.

7. Burkhard G. Uber das Lichtbogenverha1ten in Loschkammern und derem Bemessung. E1ektrie, E05, 1964, ss. 96-105.

8. Hооkе R., Jeeves Т.А. Direct seach solution оf numerical and ststist1cal problems. JACM, 1961, Е № 8, рp. 212-229.

9. Klingmаn W.R., Himmelblau D.M. Nonlinear programming with the aid of а multiple gradient summation technique. JACM, 1964, E № 11, pр.400-415.

10. Luws R., Jaakola Т.Н. Optimization bу direct search and systematic reduction оf the size оfseach region. А.1. Ch.E. Journal ,1973, E № 19, pp.760-766.

11. Rosenbrock Н.Н. Аn automatic method for finding the greatest or least value оf а funсtiоn. Соmрutеr, 1960, J.З, pp.175-184.

Введение

Задача оптимизации параметров дугогасительной камеры решается методами условной оптимизации, включающими в себя методы и процедуры безусловной или условной минимизации целевой функции по управляемым параметрам [4].

Задача нелинейного программирования, на целевую функцию которой наложены ограничения, относится к типу задач условной минимизации. Поиск точки оптимума , минимизирующей целевую функцию, производится в допустимой области S, которую образуют все , удовлетворяющие системе ограничений целевой функции.

Методы минимизации функции при нелинейных ограничениях можно разбить на два класса. К первому классу относятся те из них, в которых поиск условного минимума сводится к безусловной минимиза­ции функции, получающейся добавлением штрафа за невязки ограничений к целевой функции. В методах второго класса ограничения учитыва­ются непосредственно, и поиск идет по допустимым точкам с монотон­но убывающими значениями целевой функции. К первому классу относятся методы барьерных и штрафных функций [5]. Ко второму клас­су относятся методы прямого и случайного поиска для решения задач с ограничениями [1, 2, 3, 6, 7, 8, 9, 10, 11].

Анализ методов условной минимизации

Методы барьерных функций характерны тем, что ведут поиск решения, не выходя за пределы допустимой области. В методе барьерных функ­ций функцию штрафа подбирают так, чтобы на границе допустимого множества построить "барьер", препятствующий наруше­нию ограничений в процессе безусловной минимизации вспомогатель­ной функции по , и чтобы точки с изменением вектора управляющих параметров по некоторому правилу приближались к оптимальному значению изнутри допустимой области (множество S0 должно быть непустым).

(1)

Вспомогательная функция имеет вид:

(2)

где – вектор управляющих параметров, – вещественная функция.

Метод штрафных функций использует недопустимые точки, которые лежат вне области . Штрафная функция выбирается так, чтобы в допустимой области её вторые слагаемые принимали ненулевые зна­чения, а вне её были положительны и возрастали с увеличением невязок ограничений. Форма штрафной функции может иметь вид [5]:

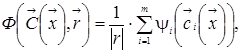(3)

где |r| – положительное число; функции определены при любом при при для ограничений типа неравенств ; при – для ограничений типа равенств.

Тогда штрафная функция имеет вид:

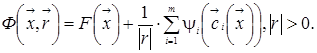(4)

Основной алгоритм со штрафными функциями формулируется так же, как алгоритм с барьерными функциями. Однако метод барьерных функций не может быть применен для решения задач с ограничениями типа равенств. Методы барьерных и штрафных функций используют процедуры безусловной минимизации, которые используют частные производ­ные целевой функции и штрафа.

Для поставленной выше задачи оптимизации параметров дугогасительной камеры, исходя из анализа и указанных ранее недостат­ков методов безусловной минимизации и ограничений применения част­ных производных второго порядка, возможно применение методов штрафных и барьерных функций совместно с методами наискорейшего спуска или методом сопряженных направлений.

Анализ методов прямого поиска

Методы прямого поиска для решения задач с ограничениями имеют те же достоинства, что и методы прямого поиска решения задач без ограничений.

Наиболее простые процедуры прямого поиска основаны на подходе Монте-Карло. Типичным примером такого подхода служит алгоритм Лууса и Якола [10]. Пусть на R-й итерации известны текущие приближения точки минимума и вектор , i-й эле­мент которого определяет область изменения соответствующей коор­динаты вектора . Генерируются j последовательных чисел , равномерно распределенных на интервале (-0,5 + 0,5), и среди точек вида:

(5)

выбирается допустимая точка , в которой целевая функция принимает наименьшее значение. Она будет новым приближением точ­ки оптимума, т.е. и новый вектор вычисляется так:

. (6)

Затем находится новый набор случайных чисел и т.д.

Применение этого простого алгоритма прямого поиска для задачи оптимизации параметров дугогасительной камеры с решеткой может оказаться неэффективным из-за широкого диапазона управляемых па­paмeтров – объема камеры и размеров решетки, т.к. это потребует многократного обращения к процедуре вычисления энергии дуги отключения при случайно заданных параметрах оптимизации. Кроме того, затруднительно определить необходимое количество набора случайных чисел, обеспечивающих достижение минимума энерговыделения в камере.

Для решения задачи оптимизации можно использовать поисковые процедуры безусловной минимизации, например, методы сеточного поиска Хука и Дживса [7] .

В тех случаях, когда ограничения задачи имеют вид:

(7)

простая отбраковка недопустимых точек может оказаться весьма эффективной, если сочетать ее с поисковой процедурой, основанной на пробных шагах вдоль координатных направлений. При сеточном поиске в процессе счета любое активное ограничение может снова стать неактивным. Задачи такого типа можно решать и методами, в которых пространство исследуется поочередным поиском минимума вдоль каждого из n взаимно ортогональных направлений [5].

Модификация сеточного поиска, позволяющая решать задачи с ограничениями, предложена Клингманом и Химмельблау [9]. Использованный ими сеточный поиск отличается от оригинального варианта тем, что выбранное сеточное направление не меняется, пока вдоль него можно уменьшать значение целевой функции. В точ­ке остановки делаются пробные шаги для определения нового направ­ления движения и т.д. В рассматриваемом алгоритме запрещены лю­бые перемещения, нарушающие ограничения задачи.

Применение сеточного метода и его модификаций в задаче минимизации энерговыделения в камере может оказаться эффективным при увеличении пробных шагов по параметрам оптимизации, особенно по объему камеры и числе пластин решетки. Это относится к начально­му периоду оптимизации, когда допустимо увеличивать длину пробных шагов и тем самым сокращать время достижения минимума энерго­выделения.

Эффективными могут оказаться прямые методы, основанные на применении барьерных функций. В методах такого типа целевая функция модифицируется внутри допустимой области, а все недопустимые точки отбрасываются. Одной из наиболее подходящих для метода прямого поиска оказалась функция Розенброка [11]. Наилучшие ре­зультаты были получены, когда барьерная функция Розенброка применялась с процедурой безусловной минимизации, предложенной им же.

Для решения задач с ограничениями существует модификация симплексного метода, в которой используются фигуры, состоящие из вершин – комплексов [6]. В ней в качестве первой вершины начального комплекса выбирается точка , лежащая внутри допустимой области. Если наряду с ограничениями общего вида известен диапазон изменения для каждого параметра вектора , то остальные вершины комплекса определяются по правилу:

(8)

где ri – псевдослучайные числа, равномерно распределенные в ин­тервале (0:1), ui, li- верхние и нижние пределы ограничений.

Полученные таким образом точки удовлетворяют ограничениям . Однако остальные ограничения задачи могут оказаться нарушенными. В этом случае недопустимая точка заменяется новой, лежащей в середине отрезка, соединяющую исходную точку и центр тяжести уже выбранных до­пустимых вершин, среди которых находится . Эта операция повто­ряется до тех пор, пока не выполняется хотя бы одно из ограниче­ний задачи. На каждой итерации заменяется самая плохая вершина комплекса, при этом она отражается относительно центра тяжести его остальных вершин. Для последовательности вершин имеем:

(9)

где α – положительный коэффициент отражения; – центр тяжести.

Если , то новая вершина оказывается по-прежнему худ­шей вершиной комплекса. В этом случае коэффициент α делится пополам. Если в результате отражения нарушается какое-то из первых 2n ограничений, то соответствующая переменная просто возвращается внутрь нарушенного ограничения. Если при отражении нарушаются другие ограничения, то коэффициент α каждый раз делится пополам до тех пор, пока точка не станет допустимой. Счет оканчи­вается, если значения целевой функции мало меняются в течение пяти последних итераций, и центр тяжести многогранника считается решением задачи.

Комплексный метод – это простой, удобный алгоритм, с успехом применяемый для решения различных задач оптимизации. Этот метод может быть успешно применен и в задаче оптимизации параметров дугогасительной камеры из-за небольшого количества параметров оптимизации и ограничений, наложенных на область допустимых зна­чений целевой функции – энергии дуги отключения. Кроме того, каж­дая итерация требует только однократного обращения к целевой функции, что может существенно уменьшить время достижения мини­мума энерговыделения в камере.

При практической реализации на ЭВМ вышеуказанных методов ус­ловной оптимизации значительная часть машинного времени тратится на строгое выполнение наложенных на целевую функцию ограничений.

Отметим основные недостатки рассмотренных методов случайного поиска (таблица 1).

Таблица 1. Количественная оценка методов минимизации

1. Для алгоритмов случайного поиска без самообучения требуется большое количество шагов поиска, т.к. предыстория процесса в этих алгоритмах не учитывается. Это приводит к существенному увеличению времени решения задачи оптимизации из-за многократного обращения к целевой функции – энергии дуги отключения и необходимости соблюдения всех ограничений, наложенных на целевую функцию.
2. Сложность определения выхода из процедур случайного поиска для всех без исключения вышеприведенных методов.
3. Существенно увеличивается машинное время при увеличении параметров оптимизации и ограничений на целевую функцию.

Выводы

Таким образом, проведенный анализ методов оптимизации применительно к условиям поставленной задачи минимизации энергии дуги при отключении тока к.з., когда минимум целевой функции определяется в широком диапазоне трех оптимизируемых параметров и ограничения по давлению в камере, показал, что наиболее подходящими для данной задачи являются те из них, которые обеспечивают достижение точки оптимального решения при меньшем числе обращений к целевой функции. На наш взгляд, наиболее подходящими для решения указанной выше задачи являются методы штрафной и барьерной функций, комплексный метод Бокса, метод скользящего допуска и случайный поиск с самообучением.

После проведения ряда вычислительных экспериментов на ЭВМ автором был принят за основу комплексный метод Бокса, который показал наиболее быструю сходимость к решению задачи оптимизации параметров ДК автоматических выключателей.

Рецензенты:

Артемьев И.Т., д.ф.-м.н., профессор, заведующий кафедрой математического и аппаратного обеспечения информационных систем ФГБОУ ВПО Чувашский государственный университет имени И.Н. Ульянова, г. Чебо­ксары.

Охоткин Г.П., д.т.н., профессор, декан факультета радиоэлектроники и автоматики ФГБОУ ВПО Чувашский государственный университет имени И.Н. Ульянова, г. Чебо­ксары.

Библиографическая ссылка