Железобетонные сжатые элементы широко распространены в практике строительства промышленных и гражданских зданий. К ним относятся несущие колонны одноэтажных и многоэтажных зданий различного назначения, опоры-стойки секционных мостов, сжатые элементы ферм (верхние пояса, стойки, некоторые раскосы) и другие элементы конструкций. Форма их поперечного сечения с точки зрения целесообразности и экономичности чаще применяется квадратной или прямоугольной, развитой в плоскости действия момента. При значительных по величине изгибающих моментах, действующих в одном направлении, поперечное сечение принимается тавровым или двутавровым. В данной научной работе рассматриваются железобетонные элементы, с прямоугольным поперечным сечением.
Сжатые железобетонные элементы рассчитываются по прочности поперечного сечения и устойчивости всего элемента как в плоскости действия момента, так и в другой плоскости, перпендикулярной к ней.
В нелинейной деформационной модели в соответствии с разделом 8 СП 63.13330.2012 используются следующиепредпосылки:
- сопротивление бетона растяжению принимают, равным нулю;
- сопротивление бетона сжатию представляется напряжениями, равными призменной прочности Rb и равномерно распределенными по сжатой зоне бетона;
- деформации (напряжения) в арматуре определяют в зависимости от высоты сжатой зоны бетона;
- растягивающие напряжения в арматуре принимают не более расчетного сопротивления растяжению Rs;
- сжимающие напряжения в арматуре принимают не более расчетного сопротивления сжатию Rsс.
Прочность прямоугольных сечений внецентренно сжатых элементов с арматурой, расположенной у противоположных в плоскости изгиба сторон сечения, при эксцентриситете продольной силы ![]() и гибкости
и гибкости ![]() определяется из условия:
определяется из условия:
![]() (1)
(1)
где Nult – предельное значение продольной силы, которую может воспринять элемент;
Asc,tot – площадь всей продольной арматуры;
φ – коэффициент, принимаемый при длительном действии нагрузки в зависимости от гибкости элемента.
Расчет на устойчивость железобетонных элементов связан с определением критической силы, при которой элемент теряет устойчивость:
![]() (2)
(2)
где l0 – расчетная длина элемента;
D – жесткость железобетонного элемента, равная:
D = kbEbI + ksEsIs, (3)
где Ebи Es – модули упругости бетона и арматуры;
I и Is – моменты инерции площадей сечения бетона и всей продольной арматуры относительно оси центра тяжести поперечного сечения элемента;
kb и ks – коэффициенты, равные:
![]() ks = 0,7; (4)
ks = 0,7; (4)
φl – коэффициент, учитывающий влияние длительности действия нагрузки:
![]() (5)
(5)
Ml1 и M1 – моменты относительно центра наиболее растянутого и наименее сжатого (при целиком сжатом сечении) стержня арматуры соответственно от действия полной нагрузки и от действия постоянных и длительных нагрузок.
δe – относительное значение эксцентриситета продольной силы:
![]() (6)
(6)
где e0– эксцентриситет приложения продольной силы;
h – высота поперечного сечения.
Для прямоугольного сечения при расположении арматуры симметрично относительно оси, проходящей через центр тяжести перпендикулярно сечению, момент инерции
- бетонного сечения
![]() (7)
(7)
- продольной арматуры
![]() (8)
(8)
Коэффициент армирования определяется выражением:
![]() (9)
(9)
откуда
![]() (10)
(10)
Подставляя выражения (4), (7) и (8) в уравнение (3) получаем выражение для жесткости железобетонного элемента прямоугольного поперечного сечения:
![]() (11)
(11)
Коэффициент α, показывающий отношение модуля упругости арматуры к модулю упругости бетона, равен:
![]() (12)
(12)
Принимая во внимание соотношения (9), (11) и (12) формула для определения критической силы (2) примет вид:
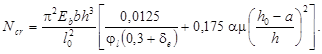 (13)
(13)
Особый интерес в уравнении (13) вызывает коэффициент φl, стоящий в знаменателе. Чтобы наглядно показать проблему, существующую в действующих нормах, вынесем коэффициент φl за скобки и подставим в него выражение (5):
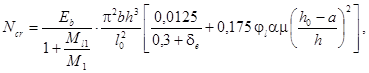 (14)
(14)
где полученное соотношение 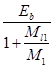 идентично выражению по снижению модуля упругости, которое тоже нормируется при учете продолжительного действия нагрузки:
идентично выражению по снижению модуля упругости, которое тоже нормируется при учете продолжительного действия нагрузки:
![]() (15)
(15)
где φb,cr – коэффициент ползучести (характеристика ползучести), принимаемый в зависимости от класса бетона по прочности и относительной влажности воздуха окружающей среды.
В теории ползучести бетона характеристика ползучести φ(t,τ) показывает отношение деформации ползучести εп(t,τ) в наблюдаемый момент времени t (t> τ) к начальным упругим деформациям бетона εу(τ), возникшим от нагрузки, приложенной в момент времени τ:
![]() (16)
(16)
В российских и европейских нормах проектирования содержится предельная величина характеристики ползучести φ∞ = φb,cr, которая отражает время t = ∞, когда деформации ползучести уже не проявляются. Следует заметить, что в СП коэффициент ползучести бетона был получен для условий, когда мгновенные деформации εм удовлетворялись закону Гука и принимались упругими (εм = εу), а коэффициент ползучести φt по диаграмме Еврокода 2 получен при напряжениях, не превышающих 45 % от прочности бетонного цилиндра в возрасте 28 сут.
Многочисленные экспериментальные исследования второй половины XX века, проведенные как в СССР, так и за рубежом, показали, что зависимость между напряжением бетона и относительной мгновенной деформацией для случая кратковременного сжатия является криволинейной с ниспадающим участком (рис. 1). К числу исследований, направленных на экспериментальное получение диаграммы мгновенного деформирования бетона, и подбор функций, описывающих данную кривую, относятся работы П.А. Лукаша, В.В. Соколовского, А. А. Прокоповича, Л. И. Онищика, А. А. Дыховичного, С.А. Тазехулахова, Г. А. Гениева, С. П. Шаха и Дж. Винтера (Surendra P. Shah, GeorgeWinter), Г. М. Штурмана (GeraldM. Sturman), А. Кабайла (A. Kabaila), Л. П. Саенза (LuisP. Saenz), Л. Г. Тулина и К. Герстла (LeonardG. Tulin,KurtH. Gerstle), М. Саржина (MuharremSargin), П. Десая и С. Кришнана (PrakashDesayi,S. Krishnan), Ж.М. Смита и Л.Е. Янга (G. M. Smith, L. E.Young) и других авторов.
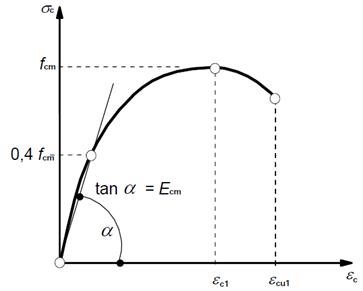
Рис. 1. Диаграмма мгновенного деформирования бетона,
нормируемая Еврокодом 2, частью 1-1
Аналитическая зависимость, аппроксимирующая данную кривую, описывается формулой Саржина, нормируемой в части 1-1 Еврокода 2[7]:
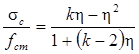 (17)
(17)
где k и η – коэффициенты, равные:
![]()
![]()
σс – напряжение бетона в момент наблюдения; εс – относительная деформация бетона;
εс1 – деформация бетона, соответствующая максимальному напряжению fсm;
εсu1 – предельная деформация бетона, соответствующая разрушению образца;
fcm – максимальное напряжение в бетоне (среднее значение прочности бетонного цилиндра при сжатии в возрасте 28 суток);
Ecm – касательный модуль упругости бетона, определенный в возрасте 28 суток.
Уравнение (17) можно записать в буквенных обозначениях, принятых в Российских нормах СП:
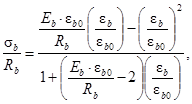 (18)
(18)
где εb0 – предельная относительная деформация бетона при равномерном осевом сжатии, равная 0,002.
Заметим, что выражение (18) никак не учитывается при определении значения Ncr по формуле (14). Неучет мгновенной нелинейности приводит к искажению конечных результатов в практических расчетах.
Опытным путем установлено, что линейная зависимость от напряжений для мгновенных деформаций и деформаций ползучести характеризует работу бетона при очень малых уровнях загружения – не более 20 % от призменной прочности бетона. При высоких уровнях загружения бетона, приближающихся к 80…90 % от предела прочности, существующие уравнения ползучести показывают существенное различие теории и эксперимента. Этот факт свидетельствует о том, что необходимо проведение дальнейших экспериментальных и теоретических исследований в теории железобетона, а именно, выведение уточненных уравнений нелинейных теорий ползучести бетона, получение предельной характеристики ползучести при совместном учете мгновенной нелинейности и нелинейной ползучести бетона, исследование напряженно-деформированного состояния сжатых элементов и совершенствование расчетов по первой и второй группах предельных состояний с учетом мгновенных нелинейных деформаций.
В работах [1, 2, 3] показан способ учета зависимости (17) в уравнениях ползучести нелинейной теории старения бетона. В частности, при описании диаграммы (см. рис. 1) полиномом пятой степени, который предложил известный специалист в теории железобетона – Байков В. Н., получено уточненное уравнение ползучести вида:
![]() (19)
(19)
где E0 – начальный модуль упругости бетона;
Ψ – новый параметр нелинейной ползучести, равный:
![]() (20)
(20)
β – коэффициент нелинейной ползучести, принимаемый по таблице Улицкого И.И.;
a, b,c,d и e – опытные коэффициенты, равные:
![]() (21)
(21)
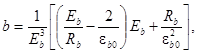 (22)
(22)
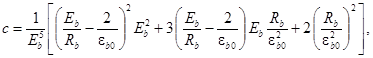 (23)
(23)
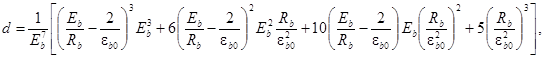 (24)
(24)

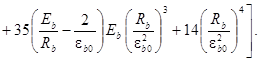 (25)
(25)
Неоспоримым достоинством теории старения по сравнению с другими теориями ползучести является то, что при ее использовании появляется возможность получить аналитическое выражение для характеристики ползучести бетона с учетом формулы Еврокода 2 (17) и нелинейной ползучести.
Решая совместно уравнение (19) и уравнение равновесия
N = Ab·σb + As·Es·ε, (26)
можно прийти к следующим разрешающим уравнениям:
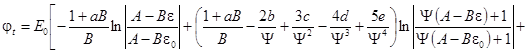
![]()
![]() (27)
(27)
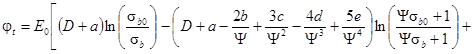
![]() (28)
(28)
где ε – продольные деформации центрально-сжатого железобетонного элемента;
σb0 – начальное напряжение в бетоне в момент времени t = 0;
σb – напряжение в бетоне в момент наблюдения;
A,B и D – постоянные коэффициенты, равные ![]()
![]() и
и ![]()
Уравнения (27) и (28) позволяют не только изучать процесс изменения характеристики ползучести бетона φt во времени с учетом мгновенной нелинейности и нелинейной ползучести бетона (при σb≥ 0,45R), но и одновременно исследовать процессы изменения напряжений в бетоне σbи арматуре σsс течением времени и устанавливать особенности перераспределения этих напряжений с учетом мгновенной нелинейности бетона.
Чтобы проанализировать влияние ползучести и мгновенной нелинейности бетонана величину критической силы, при которой сжатый железобетонный элемент теряет устойчивость, рассмотрим следующую задачу.
Условие. Железобетонная колонна длиной 10,0 м прямоугольного профиля и сплошного сечения высотой h = 50 см и шириной b = 40 см имеет шарнирное опирание на двух концах и загружена продольной постоянной силой N, приложенной со случайным эксцентриситетом равным нулю. В этом случае коэффициент δe = 0.
Найти прочность сечения Nult и величину критической силы Ncr по действующим российским нормам СП и по методике, предложенной автором, и сравнить полученные результаты.
Исходные материалы:
• бетон тяжелый класса по прочности на сжатие В15:
- призменная прочность Rb = 85 кгс/см2,
- модуль упругости Eb = 240000 кгс/см2,
• арматура класса А400:
- расчетное сопротивление сжатию Rsс = 3550 кгс/см2,
- модуль упругости Es = 2·106 кгс/см2,
- защитный слой бетона а = а’ = 4 см.
Решение
Определим расчетную длину колонны l0 и ее гибкость λ:
l0 = 1,0H = 10,0 м, ![]()
В первом приближении принимаем арматуру 2×2Ø16А400 с площадью сечения стержня 2,011 см2 и общей площадью Asc,tot = 8,04 см2.
Определяем коэффициент армирования μ по выражению (9):
![]()
Прочность сечения по формуле (1) при гибкости колонны λ = 20:
Nult = 0,7 · (85 · 2000 + 3550 · 8,04) = 0,7 · (170000 + 28542) = 138979 кгс
1. Вначале произведем расчет согласно требованиям СП [6].
Принимаем отношение ![]() тогда коэффициент φl, учитывающий влияние длительности действия нагрузки:
тогда коэффициент φl, учитывающий влияние длительности действия нагрузки:
![]()
и выражение для критической силы (14) примет вид:
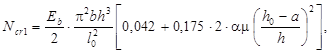
где коэффициент α определяется отношением (12):
![]()
Вычисляем величину критической силы:
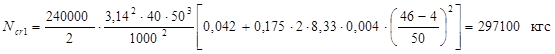
2. По предложению Байкова В. Н. и рекомендациям Еврокода 2 учтем в расчете касательный модуль полных деформаций (включая ползучесть).
Касательный модуль полных деформаций Eкас является величиной переменной и зависит от уровня загружения бетона. Для определения касательного модуля нужно знать деформации в железобетонной колонне при заданном уровне загружения:
![]()
Рассмотрим случай, когда на колонну действует нагрузка N, составляющая 80 % от предела прочности сечения, характеризующая высокий уровень загружения и область нелинейной ползучести:
N = 0,8 · 138979 = 111183 кгс.
Преобразуем уравнение (26), учитывая равенство напряжений в арматуре:
N = Ab·Eb·ε + As·Es·ε,
откуда получаем
![]()
Определим продольные деформации от действия силы N
![]()
Дифференцируя выражение (18) по переменной ε и подставляя в полученное выражение величину деформаций ε и исходные данные, получим значение касательного модуля полных деформаций Eкас = 116500 кгс/см2.
Тогда коэффициент α2 по формуле (12):
![]()
Преобразуем выражение для критической силы с учетом полученных значений:
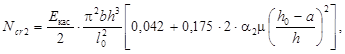
Вычисляем величину критической силы:
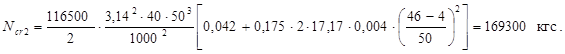
3. Расчет с учетом коэффициента ползучести φb,crв соответствии с формулой (15).
В работах [2, 3] приведены результаты кратковременных и длительных экспериментальных исследований, проведенных автором, и показан способ экспериментального получения предельной величины характеристики ползучести для бетона класса В15 с помощью уравнения (27). В соответствии с рекомендациями Еврокода 2 принимаем коэффициент φb,cr при влажности от 40 до 75 % равным 3,4.
В этом случае коэффициент φl:
φl = 1 + φb,cr, (29)
или
φl = 1 + 3,4 = 4,4.
Для наглядности сравнения учитывать касательный модуль полных деформаций не будем. Выражение для критической силы записывается следующим образом:
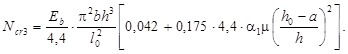
Подставляя исходные данные, определяем:
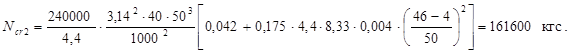
4. Расчет с учетом коэффициента ползучести φb,cr и касательного модуля Eкас.
Таким образом, имеем выражение для критической силы:
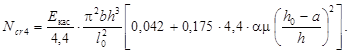
Подставляя в формулу для критической силы исходные данные и величины φb,cr и Eкас, получаем:
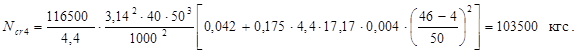
5. Уточним Ncr с учетом параметра нелинейной ползучести Ψ, полученного автором в теоретических разработках.
Коэффициент φl, учитывающий влияние длительности действия нагрузки:
φl = 1 + Ψφb,cr, (30)
где Ψ – параметр нелинейной ползучести, определяемый выражением (20).
Тогда
![]() (31)
(31)
Рассмотрим высокий уровень загружения (0,8Nult), создаваемый силой N = 111183 кгс. Параметр нелинейной ползучести β устанавливаем согласно исследованиям Улицкого И. И. – известного специалиста в области теории старения бетона:
β = 0,005.
Определим коэффициенты b и a для бетона по выражениям (21) и (22)
![]()
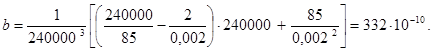
Тогда коэффициент:
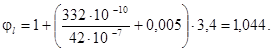
По предложению Байкова В. Н. при применении нелинейной зависимости между мгновенными деформациями и напряжениями необходимо использовать величину Eкас. Преобразуем выражение для критической силы с учетом касательного модуля полных деформаций и полученного значения коэффициента φl = 1,044:
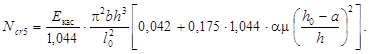
Подставляя исходные данные, определяем:
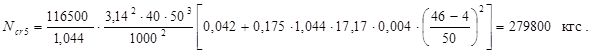
Таким образом, если взять за основу (100 %) значение критической силы, полученной в варианте № 1 (297100 кгс), то различия в результатах расчета последующих вариантов составят:
- вариант № 2 (169300 кгс) – 43 %;
- вариант № 3 (161600 кгс) – 46 %;
- вариант № 4 (103500 кгс) – 65 %;
- вариант № 5 (279800 кгс) – 6 %.
Полученные результаты указывают на необходимость учета касательного модуля полных деформаций и уточненного значения коэффициента ползучести, полученного с применением формулы (17) в расчетах железобетонных конструкций.
Рецензенты:
Веселов А.А., д.т.н., профессор кафедры железобетонных и каменных конструкций ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург.
Серов Е.Н., д.т.н., профессор кафедры конструкций из дерева и пластмасс ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург.
Библиографическая ссылка
Елистратов В.Н. К ВОПРОСУ РАСЧЕТА СЖАТЫХ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ С УЧЕТОМ МГНОВЕННОЙ НЕЛИНЕЙНОСТИ И НЕЛИНЕЙНОЙ ПОЛЗУЧЕСТИ БЕТОНА // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11801 (дата обращения: 03.03.2026).



