Уравнения динамики линейной вязко-упругой системы, у которой зависимости между деформациями и напряжениями задаются линейными соотношениями, в операторной форме можно записать следующим образом [2]:
;
. (1)
Здесь 
– вектор обобщенных сил или тензор напряжений;
u – вектор обобщенных смещений;
R – матрица или тензор инерционных характеристик;
T – матрица или тензор внешнего рассеяния энергии;
f – вектор-функция внешних нагрузок;
C – матрица или тензор упругих постоянных;
C1 – матрица или тензор коэффициентов внутреннего трения.
Граничные условия: 
на S1; 
на S2 , (2)
где 
– оператор статической совместности на поверхности тела;
– оператор геометрической совместности на поверхности тела;
– нагрузка на участке поверхности S1;
– граничное перемещение на S2.
Условие совместности по напряжениям и перемещениям на границах конечных элементов
на S1/ ;
на S2/ . (3)
Знаки «+» и «-» соответствуют различным сторонам границы сопряжения элементов S/=S1/ 
S2/.
Начальные условия
.
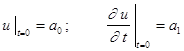Операторы D и D* сопряженные в смысле Лагранжа:
, (4)
где 
, V – объем конечного элемента.
В общем случае граница элемента S=S1S2S1/S2/.
Уравнения (1), граничные условия (2), условия совместности (3) эквивалентны условию стационарности следующего функционала [2]:
(5)
где С
=С+ р×С1, V – объем элементов, на которые разбито тело (знак суммирования в (5) по элементам, на которые разбито тело, опущен).
Вариация функционала (5) имеет вид [2]:
(6)
В случае одного независимого поля перемещений по виду вариации функционала (6) заключаем, что нагрузочные члены n и us строятся согласно выражению:
f+pRa0+Ra1+Ta0+DC1Da0,
где Rа1 – поле начальных скоростей;
PRа0 – поле начальных сосредоточенных перемещений;
f – распределенная нагрузка.
Дальнейший ход решения заключается в следующем. Поскольку все особые точки величин, преобразованных по Лапласу, находятся в левой полуплоскости, то обратное преобразование можно осуществить численным образом, положив 
. При строим амплитудо-фазо-частотные характеристики и по ним осуществляем обратное преобразование. В случае стержневой системы уравнения (1) выполняются точно, причем возможно решение задачи Коши в предположении, что известен вектор начальных перемещений u0 и вектор начальных сил σ0. Это легко сделать, т.к. рассматриваются гармонические колебания; модель одномерна, и поэтому исходные уравнения (1) являются обыкновенными дифференциальными уравнениями. В общем случае это решение можно записать в виде [2]:
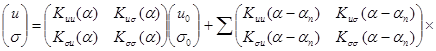(7)
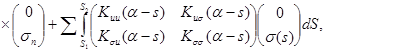
где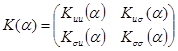 
– матрица переноса начальных параметров, элементы которой в общем случае сами являются матрицами;
К(
) – функции влияния;
– вектор нагружения в i – ом сечении стержня;
– вектор распределенных нагрузок на участке S1S2.
Рассмотрим верхнюю строку матричного соотношения (55) для начала и конца стержня. Обозначим их индексами n и k соответственно.
;
,
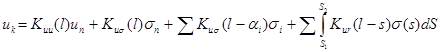где
.
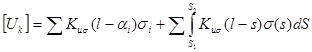Обозначив
; 
.
Для краевых усилий получим формулу [2]:
,
где А0, В0 – матрицы динамических жесткостей стержня;
[Uk] – вектор перемещений от местных нагрузок.
Рассмотрим случай соударения стержневой системы с жестким препятствием. Тогда имеем следующие граничные
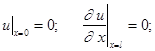
(8)
и начальные условия
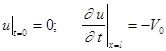. (9)
Преобразуем уравнения (1) и граничные условия (8) по Лапласу при заданных начальных условиях (9). Тогда уравнение (1) и граничные условия (8) для случая продольных колебаний запишутся следующим образом:
; (10)
,
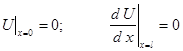где U = U(p) – преобразованные по Лапласу перемещения точек стержня; р – параметр преобразования Лапласа.
Для полученного неоднородного дифференциального уравнения решается краевая задача, заключающаяся в нахождении преобразованных по Лапласу краевых продольных сил как функций краевых перемещений.
Для этого рассмотрим однородное уравнение продольных колебаний стержня с учетом рассеяния энергии.
(11)
Обозначая
и переходя к новой переменной 
, получим вместо (11)
(12)
Если p = i
, где – частотный параметр, то
.
Решение однородного уравнения (69) имеет вид:
,
где 
.
Постоянные интегрирования с1 и с2 находим из начальных условий:
u = u0 ; N = N0,
где 
;
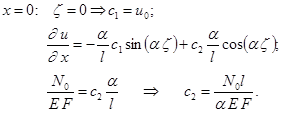
Т.е. 
;
.
Данному решению соответствует следующая матрица переноса:
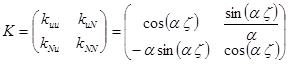. (13)
Подставив в формулы метода перемещений [1] полученные выражения для элементов матрицы переноса, получим:
; (14)
;
;
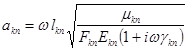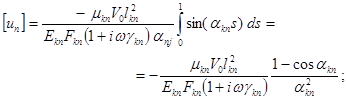
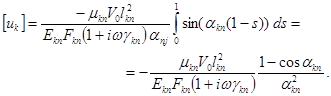
Индексы n и k указывают, соответственно, начало и конец участка стержня. А геометрические и физические константы с индексами nk и kn относятся к конкретному участку стержня.
Разбивая стержень на элементы, пользуясь формулами (14) составляются уравнения динамического равновесия узлов. Эти уравнения представляют собой систему уравнений для неизвестных узловых перемещений. Поскольку соответствующие коэффициенты получаются точным интегрированием, длина участков стержня не ограничена.
Решая полученную систему уравнений при p = i, строятся амплитудо-фазо-частотные характеристики для интересующих нас сечений стержня. Эти АФЧХ можно рассматривать как графический образ одностороннего преобразования Фурье, который совпадает с преобразованием Лапласа при импульсных воздействиях. Поскольку все особые точки соответствующих выражений лежат левее мнимой оси, обратное преобразование можно осуществлять, полагая p = i, т.е. используя построенные АФЧХ. Задача по построению АФЧХ, где в качестве силового воздействия фигурирует поле начальных скоростей, умноженное на плотность стержня, является вспомогательной. Обычно АФЧХ строятся от воздействия возмущающих сил, затем численным интегрированием или каким-либо иным способом осуществляется обратное преобразование Лапласа.
Применяя аналогичные рассуждения для дифференциального уравнения поперечных колебаний стержня на упругом основании с учетом деформаций сдвига, инерции вращения сечений и продольной силы, которое имеет вид [2]:
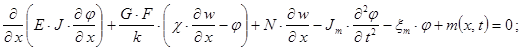
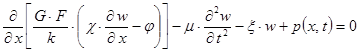, (15)
где 
и 
– коэффициенты сопротивления упругого основания линейному перемещению w и повороту сечения 
;
– момент инерции поворота поперечного сечения, м4;
– жесткость при изгибе;
– жесткость при сдвиге;
k – коэффициент, зависящий от формы поперечного сечения и характеризующий распределение касательных напряжений при сдвиге;
;
N – продольная сила, Н;
m(x, t) – распределенный изгибающий момент;
p(x, t) – распределенная поперечная нагрузка, Н.
Получим формулы для тонкого стержня:
;
;
;
; (16)
;
;
где 
; 
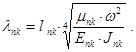
Найдем величины, зависящие от нагрузки по длине стержня и определяющие правые части разрешающих уравнений:
;
;
;
.
Данный подход был реализован, аналитически и экспериментально проверен при решении различных задач поперечных и продольных колебаний стержней и стержневых систем, а также при решении задачи динамики ковочного молота как сложной стержневой системы, испытывающей ударные нагрузки в работах [3, 4, 5].
Рецензенты:
Лебедев А.М., д.т.н., доцент, профессор Ульяновского высшего авиационного училища (института), г. Ульяновск.
Антонец И.В., д.т.н., профессор Ульяновского государственного технического университета, г. Ульяновск.
Библиографическая ссылка
Санкин Ю.Н., Юганова Н.А. НЕСТАЦИОНАРНЫЕ КОЛЕБАНИЯ СТЕРЖНЕВЫХ СИСТЕМ // Современные проблемы науки и образования. – 2013. – № 6. ;URL: https://science-education.ru/ru/article/view?id=11783 (дата обращения: 19.04.2024).