Введение
Под сетевыми системами в рамках данной статьи будем понимать совокупность распределенных программно-управляемых систем обменивающихся информационным трафиком посредством стека IP-протокола. Такие сетевые системы предоставляют основной спектр нынешних Интернет-услуг и предъявляют различные требования к их качеству, которое принято называть QoS (Quality of Service, качество обслуживания). Современные механизмы QoS опираются на принципы либо интегрированной архитектуры обслуживания (Integrated Services, IntServ), которая описана в руководстве IETF RFC1633, либо на принципы архитектуры дифференцированного предоставления обслуживания (Differentiated Services, DiffServ), которая описана в руководстве IETF RFC2474. Архитектура IntServ обеспечивает сетевое обслуживание в двух режимах: 1) контролируемой загрузки (Controlled Load, CL) для обеспечения гарантированного трафика к сетевым адаптивным приложениям «мягкого» реального времени; 2) гарантированного обслуживания (Guaranteed Service, GS) с обеспечением заранее заданной полосы пропускания к сетевым неадаптивным приложениям «жесткого» реального времени.
В случае CL для настройки услуг не используются управляющие параметры QoS, такие как уровень потерь пакетов и время задержки поступления данных. Доставка трафика сетевому приложению зависит лишь от времени задержки ретрансляции данных сетевым оборудованием, а также от всплескового характера самого трафика. Время минимальной задержки в режиме CL, будет стремиться к максимальной величине всплескового (в количественном отношении) объема трафика. В случае обеспечения уровня услуг GS сетевому приложению выделяется гарантированная полоса пропускания трафика и регулируется граничное значение времени задержки обслуживания. Величина максимального времени задержки зависит от параметров канала передачи данных, от дисциплины, интенсивности обслуживания и определена в руководстве IETF RFC2212 и алгоритмом маркерной корзины (Token Bucket):
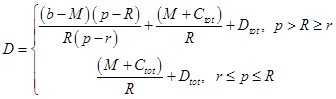 (1)
(1)
где r – интенсивность поступления маркеров в корзину, байтов/c;
p – максимальная интенсивность поступления данных, байтов/с;
R – интенсивность обслуживания, байтов/с;
b – размер маркерной корзины, байтов;
М – максимальный размер поступающего блока данных (IP-дейтаграммы), байтов;
С – максимальная девиация размера поступающего блока данных, байтов;
D –максимальная девиация времени при обработке данных устройствами обслуживания, с.
В дополнение к рассмотренной, архитектура DiffServ осуществляет разделение трафика на классы и приоритеты. В целом, при управлении качеством обслуживания в IP-сетях основное внимание уделяется обеспечению минимальных (или максимальных) гарантированных значений параметров управления трафиком: полосой пропускания, временной задержкой, девиацией временной задержки и уровнем потерь блоков данных. Поэтому одними из современных адекватных математических моделей сетевых систем с гарантированным обслуживанием являются модели, построенные на (min,+) или (max,+) алгебраических структурах, а развитие такого подхода для оценки производительности сетевых систем, называется «network calculus» [9]. Данное направление базируется на подходах теории алгебраических структур – полуколец с каноническим упорядочиванием (идемпотентных полуколец, диоидов) [8] идемпотентного анализа [3], моделирования дискретных динамических систем [6]. Моделированию и оценке гарантированной производительности и надежности сетевых систем посвящены работы c участием автора [1,2,4,5].
Элементы теории: (min,+) алгебра и network calculus
Основной алгебраической структурой в рассматриваемом подходе является структура, называемая «диоид» [8]. Диоид ![]() определяется, как числовое множество
определяется, как числовое множество ![]() , снабженное двумя замкнутыми операциями: «сложение,
, снабженное двумя замкнутыми операциями: «сложение, ![]() » и «умножение,
» и «умножение, ![]() »,
», ![]() . Операции в диоиде должны подчиняться следующим правилам: 1) ассоциативность по сложению и умножению; 2) коммутативность по сложению; 3) дистрибутивность по умножению, относительно сложения; 4) существование нейтральных элементов для обеих операций: нулевого (по сложению и поглощающего по умножению) и единичного; 5) идемпотентность сложения; 6) отсутствие обратных элементов.
. Операции в диоиде должны подчиняться следующим правилам: 1) ассоциативность по сложению и умножению; 2) коммутативность по сложению; 3) дистрибутивность по умножению, относительно сложения; 4) существование нейтральных элементов для обеих операций: нулевого (по сложению и поглощающего по умножению) и единичного; 5) идемпотентность сложения; 6) отсутствие обратных элементов.
В рамках статьи будем рассматривать операции диоида![]() ,
, ![]() следующим образом. Для функций
следующим образом. Для функций ![]() ,
, 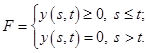 , а для
, а для ![]() ,
, ![]() ,
, 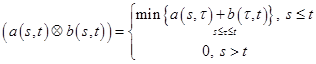 . Рассмотренная алгебраическая структура, диоид позволяет предложить достаточно эффективный подход к аналитическому и имитационному моделированию сетевых систем, наряду с теорией массового обслуживания (ТМО). Существенные отличия подходов, в целом, состоят в том, что в ТМО для расчета числовых характеристик необходимо построить аналитические или адекватные им приближенные модели входных потоков и элементов обслуживания, а в алгебраическом подходе «network calculus» исследуются граничные условия для кумулятивных функций, описывающих как входной поток, так и поток обслуживания. Таким образом, в последнем подходе, элемент обслуживания служит фильтром входного потока, придавая выходному потоку ту, или иную заданную форму. Отметим, что функции, описывающие граничные условия могут быть как детерминированными, так и случайными [9].
. Рассмотренная алгебраическая структура, диоид позволяет предложить достаточно эффективный подход к аналитическому и имитационному моделированию сетевых систем, наряду с теорией массового обслуживания (ТМО). Существенные отличия подходов, в целом, состоят в том, что в ТМО для расчета числовых характеристик необходимо построить аналитические или адекватные им приближенные модели входных потоков и элементов обслуживания, а в алгебраическом подходе «network calculus» исследуются граничные условия для кумулятивных функций, описывающих как входной поток, так и поток обслуживания. Таким образом, в последнем подходе, элемент обслуживания служит фильтром входного потока, придавая выходному потоку ту, или иную заданную форму. Отметим, что функции, описывающие граничные условия могут быть как детерминированными, так и случайными [9].
Далее рассматриваем детерминированные функции фильтрации входного трафика. На рис. 1 показана иллюстрация к такому подходу, где ![]() – входной фильтрованный поток (входная кумулятивная функция),
– входной фильтрованный поток (входная кумулятивная функция), ![]() – поток обслуживания (выходная кумулятивная функция), а часть обозначений соответствует формуле (1). Буфер сетевых данных принимает входной поток
– поток обслуживания (выходная кумулятивная функция), а часть обозначений соответствует формуле (1). Буфер сетевых данных принимает входной поток ![]() , который на физическом уровне IP-сети является последовательным байтовым потоком, составляющим накапливаемый (следовательно, кумулятивный) объем данных, и, в целом – входной трафик. Далее поток подвергается
, который на физическом уровне IP-сети является последовательным байтовым потоком, составляющим накапливаемый (следовательно, кумулятивный) объем данных, и, в целом – входной трафик. Далее поток подвергается ![]() - фильтрации, то есть в техническом отношении при информационной перегрузке, переполнении входных буферов, различных неисправностях программно-аппаратного обеспечения, при выполнении функций QoS, разделении и трафика на классы и приоритеты происходит отсекание части трафика, подобно прохождению сигналов через фильтры. Так формируется входной фильтрованный поток
- фильтрации, то есть в техническом отношении при информационной перегрузке, переполнении входных буферов, различных неисправностях программно-аппаратного обеспечения, при выполнении функций QoS, разделении и трафика на классы и приоритеты происходит отсекание части трафика, подобно прохождению сигналов через фильтры. Так формируется входной фильтрованный поток ![]() , поступающий на устройство обслуживания, которое в свою очередь также имеет
, поступающий на устройство обслуживания, которое в свою очередь также имеет ![]() - фильтр с характеристиками, зависящими от применяемого в сетевом устройстве алгоритма маркерной корзины (Token Bucket). В итоге формируется выходной поток
- фильтр с характеристиками, зависящими от применяемого в сетевом устройстве алгоритма маркерной корзины (Token Bucket). В итоге формируется выходной поток ![]() .
.
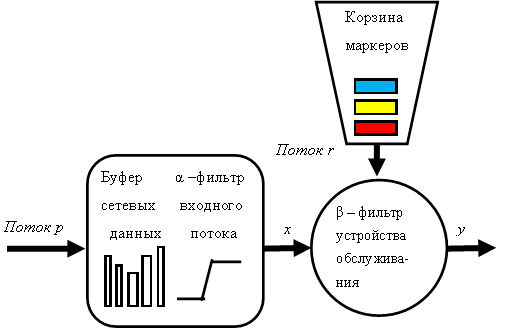
Рис. 1. Имитационная модель сетевой системы с (min,+) фильтрацией
Математической моделью рассматриваемого (min,+) подхода являются уравнения:
для ![]()
![]() ; (2)
; (2)
для ![]()
![]() . (3)
. (3)
Поиск решения уравнений (2) и (3) приводит к известной из теории цифровой обработки информации задаче о вычислении интеграла свертки:
![]() , (4)
, (4)
а в терминах рассматриваемого подхода
![]() . (5)
. (5)
Метод расчета![]() (min,+) интегральной свертки
(min,+) интегральной свертки
В работе автора [5] предложен подход к реализации алгоритмов network calculus на функциональном языке программирования J и были даны необходимы описания входных кумулятивных функций. Рассмотрим дальнейшее описание имитационных алгоритмов расчета![]() (min,+) интегральной свертки на функциональном языке программирования J.
(min,+) интегральной свертки на функциональном языке программирования J.
В вышеуказанном языке программирования есть оператор min, обладающая всеми необходимыми для названных ранее операций «сложение, ![]() » и «умножение,
» и «умножение, ![]() » свойствами. Оператор min может быть применим, как к скалярным, так и к матричным величинам. Для скалярных величин можно в среде программирования J ввести с клавиатуры, например: 4 min 5, ((35 min 24) min 4). Можно проверить свойство дистрибутивности операции: ((3 min 2) + 4) = (3 + 4) min (2 + 4), результатом будет вывод на экран числа 1, что означает истинность выражения (если результат равен 0, то выражение не является истинным). Матричные операции в (min,+) алгебре
» свойствами. Оператор min может быть применим, как к скалярным, так и к матричным величинам. Для скалярных величин можно в среде программирования J ввести с клавиатуры, например: 4 min 5, ((35 min 24) min 4). Можно проверить свойство дистрибутивности операции: ((3 min 2) + 4) = (3 + 4) min (2 + 4), результатом будет вывод на экран числа 1, что означает истинность выражения (если результат равен 0, то выражение не является истинным). Матричные операции в (min,+) алгебре
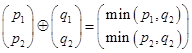 и
и 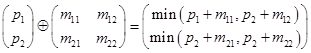
в языке программируются соответственно: P min”0 Q и P (min”1 .+) M.
Для расчетов (поточечного) минимума двух функций ![]() и их свертки
и их свертки ![]() в языке J нужно запрограммировать соответственно: min@(f@t, g@t) и min@(f@s, g@(t-s)).
в языке J нужно запрограммировать соответственно: min@(f@t, g@t) и min@(f@s, g@(t-s)).
Теперь опишем главный результат статьи – программную реализацию основного уравнения баланса сетевой модели. Уравнение Линдли [7] (аналогично ТМО):
![]()
На функциональном языке J реализовано следующей программой:
cocurrent < ’LINDLEY’
ylist =: rhs0
c =: >@lhs1
xlist =: >@lhs2
ind =: <:@#@ylist
xnext =: ind { xlist
yprev =: {:@ylist
ynext =: max0 @ xnext + yprev + c
cocurrent <’base’
lindley_z_ =: ylist_LINLEY_,ynext_LINDLEY_
Заключение
Анализ в области имитационного моделирования сетевых систем показал, что методы, построенные на основе алгебраического подхода с использованием кумулятивных функций входных и выходных потоков, представляются очень перспективными и вполне соответствуют технологическим особенностям оборудования, применяемого в современных IP-сетях. Выбор в качестве программной реализации весьма нераспространенного функционального языка программирования J и реализованные на нем алгоритмы имитационного моделирования также показали эффективность исполнения алгоритмов за счет внутренней рекурсивной организации самого языка программирования. В связи с этим, можно сделать вывод об адекватности применения математического и программного инструментария для имитационного моделирования сетевых систем для оценки их производительности.
Рецензенты:
Павлов И.В., д.ф.-м.н., профессор, заведующий кафедрой высшей математики Ростовского государственного строительного университета, г. Ростов-на-Дону.
Чернов А.В., д.т.н., профессор, заведующий кафедрой прикладной математики и вычислительной техники Ростовского государственного строительного университета, г. Ростов-на-Дону.
Библиографическая ссылка
Чубейко С.В. АЛГОРИТМЫ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ДЛЯ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ СЕТЕВЫХ СИСТЕМ НА ОСНОВЕ (MIN,+) ФИЛЬТРАЦИЙ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11545 (дата обращения: 03.03.2026).



