Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Чернов А.В. 1 Сергеева Е.А. 2

---

1 ФГБОУ ВПО «Ростовский государственный строительный университет»

2 ФГБОУ ВПО «Ростовский государственный университет путей сообщения»

В статье предложен метод определения неисправностей типа «постоянный 0» и «постоянная 1» в цифровых комбинационных схемах. Подробно рассмотрен подход к тестированию цифровых комбинационных схем, основанный на вычислении тестового «синдрома» для логических функций. Обозначены преимущества и недостатки подхода, связанного с синдромным тестированием. Приведены необходимые математические выражения тестового синдрома, а также рекурсивная процедура его вычисления. Рассмотрено преобразование Уолша с матрицей Адамара для спектрального представления булевых функций. Показан пример расчета преобразования Уолша с матрицей Адамара для конкретной булевой функции. Указана связь между рассматриваемым спектральным преобразованием и тестовым синдромом. Приведено выражение расчета тестового синдрома по спектральному коэффициенту. Показан пример, позволяющий выявить недостатки тестового синдрома. Разработан метод составления тестовых векторов, использующий свойства автокорреляционной функции булевой функции. В автокорреляционном тестировании доказано утверждение, применимое для тестирования рассматриваемого класса неисправностей в цифровых комбинационных схемах.

Статья в формате PDF

152 KB

автокорреляционное тестирование

автокорреляционная функция булевой функции

тестовый синдром

комбинационная схема

булева функция

1. Ахмед Н. Ортогональные преобразования при обработке цифровых сигналов / Ахмед Н., Рао К.Р.: Пер. с англ. –М.: Связь. – 1980. – 248с.

2. Гуда А.Н. Алгоритмы спектральных и символьных преобразований булевых функций для решения задач анализа и проектирования технологически безопасных информационных систем // Гуда А.Н., Чернов А.В. // Вестник Ростовского государственного университета путей сообщения. – 2008. – №2. – С. 46-53.

3. Карповский М.Г. Спектральные методы анализа и синтеза дискретных устройств. Библиотека по автоматике, выпуск 507 / Карповский М.Г., Москалев Э.С. – Л., «Энергия». – 1973. – 144 с.

4. Чернов А.В. Спектральные преобразования дискретных функций для вычисления логических производных / Чернов А.В., Калинин Т.С. // Обозрение прикладной и промышленной математики. – 2010. – Т.17, №6. – С. 1049-1051.

5. Aborhey S. Autocorrelation testing of combinational circuits / Aborhey S. // Computers and Digital Techniques, IEE Proceeding E. – 1989. – V. 136, issue 1. – PP. 57-61.

6. Eris E. Syndrome and autocorrelation-testable internally unate combinational networks / Eris E., Muzio J.C. // Electron. Lett. – 1984. –№20, (6). –PP. 264-266.

7. Savir J. Syndrome-testable design of combinational circuits / Savir J. // IEEE Trans. Com-put. – 1980. – C-29. – PP. 442-451.

8. Tarannikov Y., Autocorrelation coefficients and correlation immunity of Boolean functions / Korolev P., Botev A. // Advances in Cryptology ASIACRYPT – 2001, Lecture Notes in Computer Science 2248. – Springer-Verlag. – РР. 460-480.

Введение

Комбинационные схемы являются основой построения всех современных цифровых устройств обработки информации. Усложнение самих цифровых устройств, высокая степень их интеграции естественным образом усложняют задачи их тестирования и, конечно, полностью исключают переборные методы тестирования. Пути поиска компактных тестов для цифровой аппаратуры без снижения полноты и глубины тестирования были обозначены достаточно давно. Одним их подходов компактному тестированию и синтезу цифровых схем [3], а также к исследованию булевых функций в области криптографии [8] является их представление в виде наборов спектральных коэффициентов преобразования Уолша (в общем виде Адамара-Радемахера-Уолша, так как используются различные матрицы для преобразования). Данное преобразование хорошо исследовано и для него разработаны различные алгоритмы быстрых преобразований [1]. Автором в работах [2,4] рассматривались спектральные преобразования Уолша для булевых функций, применительно к некоторым задачам технической диагностики. Отметим также, что в рамках данной статьи под тестированием понимается выявление лишь константных неисправностей вида «постоянный 0» и «постоянная 1».

Тестовый «синдром» и спектральное преобразование

Особенностью спектрального представления булевых функций является не только компактность самого теста, но и возможность непосредственного встраивания тестов в цифровое устройство для решения задач онлайновой диагностики и самодиагностики. Идея составления теста по спектральному преобразованию булевой функции восходит к работе [7], в которой предложен тестовый «синдром» (в дальнейшем без кавычек), назначением которого является различение логической функции, описывающей исправное устройство, от логической функции, измененной под воздействием возникшей в устройстве неисправности. В работе [7] тестовый синдром определен для трех логических операций (,, – исключающее ) как отношение числа минитермовбулевой функции, содержащей только одну операцию к , то есть , где означает число входов функции. Таким образом, синдром является некоторым числом, характеризующим функцию в зависимости от базиса её представления и рассчитывается для логических функций, содержащих только одну логическую операцию со значениями , .:

1) для многовходового логического синдром (1)

2) для многовходового логического синдром; (2)

3) для многовходового логического – синдром . (3)

Синдром , получающийся в результате объединения двух синдромов , разными операциями зависит от её вида:

1) рассчитывается ; (4)

2) рассчитывается ; (5)

3) рассчитывается; (6)

4) рассчитывается . (7)

Для всей комбинационной схемы, реализуемой функцией, для тестирования входана изменение его значения на константу 0 или 1, существует её представление:

,

где – выражения, не зависящие от,

а «синдром» . (8)

Процедура расчета комбинационной схемы с помощью представленного синдрома следующая. Начиная с представления схемы в виде булевой функции в дизъюнктивной нормальной форме рекурсивно применять формулы (1)-(8), исключая каждый раз по одной входной переменной. Такой расчет возможен в онлайновом режиме и не требует формирования и сохранения множества тестовых векторов, хотя требует дополнительных ячеек памяти и выходов комбинационной схемы. Также, такой синдром оказывается не применимым к некоторым видам схем. Для преодоления этих недостатков были предложены методы тестирования схем, использующие свойства спектральных преобразований булевых функций.

Спектральное преобразование булевой функции выполняется следующим образом. Зададим булеву функцию в векторном виде , где – число входных значений. Преобразование Уолша в общем случае имеет вид

, (9)

где – матрица размерности , зависящая от вида выбираемого преобразования.

В данной статье выберем матрицу Адамара и приведем пример для конкретной булевой функции .Выходной вектор функции равен . Выполним -точечное преобразование Уолша-Адамара с матрицей Адамара:

.

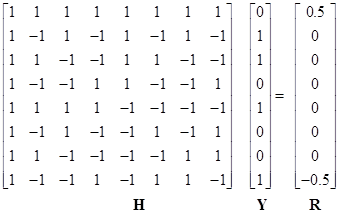В результате булева функция представлена вектором спектральных коэффициентов .В работе [6] указана формула расчета синдромабулевой функции ,:

, (10)

где , для .

Решение о неисправности схемы принимается из условия , где – функция исправной схемы, – функция, измененная в результате неисправности. Также в [6], показано, что спектральный коэффициентпреобразования Уолша (без множителя ) связан с синдромом:

. (11)

Ранее было указано, что синдромное тестирование не применимо к некоторым видам комбинационных схем. Для иллюстрации возьмем приведенную выше в примере функцию и рассчитаем синдром. Выходной вектор ,, и по (11) . Теперь положим, что в схеме есть константная неисправность.Тогда ,, , , и по (11) .Синдромы равны между собой и неисправность определить нельзя, поэтому необходимо усовершенствовать данный метод.

Автокорреляционное тестирование и основной результат

В приведенном выше примере, функция с внесением неисправности представляет собой функцию логического , которую вправе можно назвать одной из «трудно тестируемых» функций. Для достижения тестируемости функций такого вида предлагается применение автокорреляционного тестирования с возможностью различения типа неисправности.

Автокорреляционная функция [5] для -аргументной булевой функции определяется как

.

Выразим автокорреляционную функцию в терминах спектральных коэффициентов и, где . Из преобразования Уолша-Адамара , получаем

и .

Найдем значение выражения

.

.

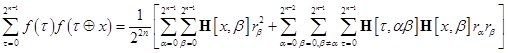Тогда

, (12)

где –-й спектральный коэффициент.

В автокорреляционном тестировании автокорреляционная функция исправной комбинационной схемы сравнивается с автокорреляционной функцией комбинационной схемы с неисправностью.

Докажем

Утверждение

Неисправность типа «постоянный 0» либо «постоянная 1» обнаруживается, если для ,, для спектральных коэффициентов исправной функции и спектральных коэффициентов функции с -й неисправностью

.ÿ

Доказательство

Из выражения (12) следует, что для функции без неисправности автокорреляционная функция выражается

.

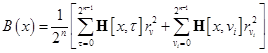Для функции с неисправностью автокорреляционная функция будет

.

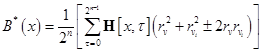Заметим, что из-за возникновения неисправности .Вычтем и получаем

.■

Рассмотрим пример: для булевой функции автокорреляционные функции, предназначенные для тестирования неисправностей вида «константный 0» и «константная 1» будут

, ,, ,,

а в матричном виде тестовые вектора .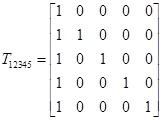

Работа выполнена при финансовой поддержке РФФИ, проекты 13-01-00325-а, 13-01-00637-а.

Рецензенты:

Беляков С.Л., д.т.н., профессор кафедры информационно-аналитических систем безопасности Южного федерального университета, г. Таганрог.

Бутакова М.А., д.т.н., профессор кафедры информатики ФГБОУ ВПО Ростовский государственный университет путей сообщения, г. Ростов-на-Дону.

Библиографическая ссылка