Введение
Задачи создания оптимальных режимов управления возникают в самых различных прикладных областях. Фундаментальный математический аппарат теории оптимального управления, такой как принцип максимума Л.С. Понтрягина, метод динамического программирования Р. Беллмана и др., не всегда эффективен при решении задач с нелинейными объектами и функционалами общего вида. Поэтому, наряду с теоретическими исследованиями, важное практическое значение имеет разработка численных методов решения задач оптимального управления.
Рост производительности вычислительной техники обусловил создание такого класса вычислительных методов, как эволюционные алгоритмы [3], [5]. Сегодня генетические алгоритмы успешно используются для поиска оптимального решения в задачах идентификации [4], [6], оптимизации параметров регуляторов[7] и др. В традиционных генетических алгоритмах [3]-[7] область поиска состоит из векторов возможных решений, размерность которых зависит от количества дискретных моментов времени, что влечет за собой определенные временные и вычислительные затраты.
В настоящей работе представлен новый метод, предназначенный для численного решения задачи оптимального управления. Метод получил название вариационного генетического алгоритма. Метод состоит в задании одного базисного решения из конечного числа значений управления в дискретные моменты времени и множества малых вариаций этого базисного решения. Все генетические операции [1] выполняются с множеством вариаций базисного решения. В предложенном алгоритме каждая вариация описывается вектором из трех компонент. Первая компонента указывает на номер точки вариации или момент времени, где необходимо производить вариацию базисного решения. Вторая компонента указывает величину изменения базисного решения. Третья компонента указывает на количество соседних точек, в которых малое изменение базисного обратно пропорционально расстоянию до точки вариации.
Использование вариационного генетического алгоритма по сравнению с классическим подходом позволяет уменьшить область поиска оптимального решения за счет задания базисного решения, а также уменьшить время поиска за счет работы с векторами вариаций небольшой размерности. Метод позволяет сократить объем используемой памяти за счет замены множества возможных решений, состоящих из векторов, размерность которых зависит от количества дискретных моментов времени, на один такой вектор, описывающий базисное решение, и множество векторов вариаций малой размерности.
Постановка задачи
Задана математическая модель объекта управления
![]() , (1)
, (1)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() – ограниченное замкнутое множество.
– ограниченное замкнутое множество.
Задано начальное состояние
![]() . (2)
. (2)
Задано терминальное состояние в форме ![]() мерного многообразия
мерного многообразия
![]() ,
, ![]() , (3)
, (3)
где ![]() – время управления, определяемое выполнением условия (3)
– время управления, определяемое выполнением условия (3)
Заданы критерии качества управления
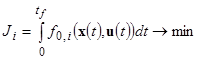 ,
, ![]() . (4)
. (4)
Решением численной задачи многокритериального оптимального управления является множество Парето
![]() , (5)
, (5)
где ![]() ,
, ![]() .
.
При подстановке ![]() в модель объекта управления (1) решение системы уравнений
в модель объекта управления (1) решение системы уравнений
![]() (6)
(6)
приводит к получению Парето оптимальных значений функционалов (4)
![]() . (7)
. (7)
![]()
![]() ,
, ![]() .
.
Задача состоит в нахождении по критериям (4) управления в виде функций времени
![]() . (8)
. (8)
Искомые функции должны удовлетворять ограничениям на управление ![]() ,
, ![]() и принадлежать классу кусочно-непрерывных функций
и принадлежать классу кусочно-непрерывных функций ![]() .
.
Метод вариации управления
Задаем множество значений моментов времени
![]() , (9)
, (9)
где
![]() . (10)
. (10)
Согласно разработанному методу необходимо выбрать базисное решение. Определим базисное решение в виде упорядоченного множества допустимых значений управления в дискретные моменты времени
![]() , (11)
, (11)
где
![]() . (12)
. (12)
Определим вариацию базисного решения. Для построения вариации выбираем точку действия вариации ![]() и величину вариации
и величину вариации ![]() . Соседние
. Соседние ![]() точек слева и справа от точки
точек слева и справа от точки ![]() также подвергнем вариации пропорционально их близости к точке действия вариации
также подвергнем вариации пропорционально их близости к точке действия вариации ![]() .
.
Существенным обстоятельством является размерность управления. Необходимо установить, как осуществлять вариацию при многомерном управлении: либо варьировать все компоненты управления в выбранный момент времени ![]() , либо выбирать по величине
, либо выбирать по величине ![]() и компоненту управления и момент времени для вариации.
и компоненту управления и момент времени для вариации.
При построении малых вариаций используем принцип наименьшей вариации, чем меньше вариация, тем лучше сходимость алгоритма. Поскольку вариация всех компонент управления является совокупностью вариаций одной компоненты, то на основании принципа малых вариаций устанавливаем правило выполнения вариации, по которому определяем по величине ![]() компоненту вектора управления и момент времени для вариации.
компоненту вектора управления и момент времени для вариации.
Выбираем случайно целое число ![]() из множества целых чисел величиной от 0 до
из множества целых чисел величиной от 0 до ![]() ,
,
![]() . (13)
. (13)
Определяем компоненту управления для вариации как остаток от деления величины ![]() на количество
на количество ![]() точек в решении
точек в решении
![]() , (14)
, (14)
где ![]() – целая часть числа
– целая часть числа ![]() .
.
Определяем точку вариации
![]() , (15)
, (15)
Выполняем вариацию для компоненты ![]() базисного решения.
базисного решения.
В результате действия вариации получаем новое возможное решение
![]() , (16)
, (16)
![]() , (17)
, (17)
![]()
![]() , (18)
, (18)
![]()
![]() . (19)
. (19)
где ![]() – скалярная величина приращения компоненты
– скалярная величина приращения компоненты ![]() управления,
управления, ![]() – диапазон вариации.
– диапазон вариации.
Целочисленная величина диапазона вариации ![]() указывает на количество точек слева и справа от точки вариации
указывает на количество точек слева и справа от точки вариации ![]() , в которых управление также подвергается вариациям на величины обратно пропорциональные удаленности от точки вариации
, в которых управление также подвергается вариациям на величины обратно пропорциональные удаленности от точки вариации ![]() .
.
Графическое изображение вариации управления при глубине вариации ![]() представлено на рис. 1.
представлено на рис. 1.
При выполнении вариации используем приращения управления ![]() , точку действия вариации
, точку действия вариации ![]() , диапазон вариации
, диапазон вариации ![]() .
.
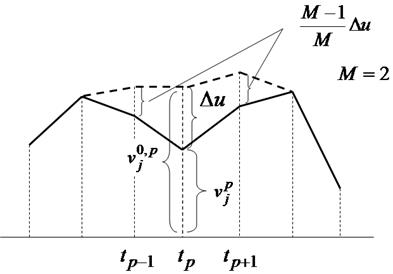
Рис. 1 Вариация управления
С целью повышения эффективности поиска нормируем величины управления
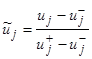 , (20)
, (20)
где ![]() – величина компоненты
– величина компоненты ![]() нормированного управления.
нормированного управления.
Для нормированного управления все компоненты имеют одинаковые ограничения
![]() ,
, ![]() . (21)
. (21)
Обратный пересчет величины реального управления ![]() по величине нормированного управления
по величине нормированного управления ![]() выполняем по формуле
выполняем по формуле
![]() . (22)
. (22)
Для нормированного управления получаем одинаковые ограничения для всех значений управлений. Положительная величина приращения управления не зависит от номера компоненты управления, поэтому ищем одно положительное значение приращения ![]() для всех компонент управления. Непосредственно компоненту управления, на которую это приращение действует, определяем из соотношения (14).
для всех компонент управления. Непосредственно компоненту управления, на которую это приращение действует, определяем из соотношения (14).
![]() . (23)
. (23)
При описании вариации используем вектор размерностью ![]()
![]() , (24)
, (24)
где ![]() ,
, ![]() ,
, ![]() .
.
Согласно методу действие вектора вариаций (24) на базисное решение (11) приводит к получению нового решения
![]() , (25)
, (25)
где ![]() .
.
Поиск решения осуществляем на множестве наборов векторов вариаций
![]() , (26)
, (26)
где
![]() . (27)
. (27)
Любое новое возможное решение является следствием воздействия набора вариаций на базисное решение
![]() ,
, ![]() . (28)
. (28)
Пусть значения векторов вариаций во всех наборах (26) неизменны. Тогда поиск решения осуществляем в форме оптимального набора векторов вариаций (27). Набор (27) векторов вариаций называем структурной частью вариации.
Значения самих векторов вариаций (24) называем параметрической частью вариации. Поиск новых возможных решений целесообразно осуществлять на пространствах структурных и параметрических частях вариаций.
Для поиска решения используем метод генетического алгоритма. При получении новых возможных решений выполняем генетические операции скрещивания и мутации для структурных и параметрических частей.
Пример управления нелинейной системой Дуффинга
Рассмотрим пример решения задачи оптимального управления с фазовыми ограничениями с помощью вариационного генетического алгоритма.
В качестве объекта управления задана нелинейная система Дуффинга [2]
![]() , (29)
, (29)
![]() , (30)
, (30)
где на управление ![]() наложены ограничения
наложены ограничения
![]() . (31)
. (31)
Критерий качества определен функционалом быстродействия
![]() , (32)
, (32)
где ![]() – время окончания процесса управления.
– время окончания процесса управления.
Заданы терминальные условия
![]() , (33)
, (33)
![]() . (34)
. (34)
В пространстве координат ![]() ,
, ![]() заданы области, области, определяющие фазовые ограничения
заданы области, области, определяющие фазовые ограничения
![]() , (35)
, (35)
![]() . (36)
. (36)
Необходимо найти оптимальное управление ![]() , удовлетворяющее ограничениям (31), такое, чтобы решение системы (29), (30) с заданными начальными значениями
, удовлетворяющее ограничениям (31), такое, чтобы решение системы (29), (30) с заданными начальными значениями
![]() , (37)
, (37)
![]() , (38)
, (38)
в незаданный конечный момент времени ![]() удовлетворяло терминальным условиям (33), (34)
удовлетворяло терминальным условиям (33), (34)
![]() , (39)
, (39)
![]() , (40)
, (40)
и минимизировало значение функционала (32) и не должно попадать в область ограничений (35), (36).
![]() ,
, ![]() , (41)
, (41)
![]() ,
, ![]() . (42)
. (42)
Для удовлетворения ограничениям введем в критерий качества функцию штрафа. Функция должна увеличивать значение критерия (32) в случае нарушения условий (41), (42). Для придания чувствительности функции штрафа к характеру нарушения условий (41), (42) используем расстояние от текущей точки до границ областей (35), (36).
Критерий качества с учетом функции штрафа имеет вид
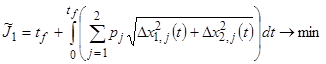 , (43)
, (43)
где
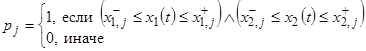 , (44)
, (44)
![]() ,
, ![]() ,
, ![]() , (45)
, (45)
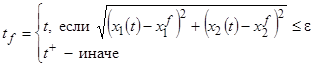 , (46)
, (46)
![]() – максимальное время процесса управления,
– максимальное время процесса управления, ![]() – заданная терминальная точность.
– заданная терминальная точность.
При поиске решения используем генетический алгоритм многокритериальной оптимизации. Вторым критерием считаем точность выполнения терминальных условий:
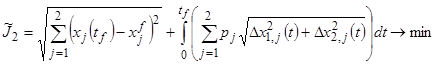 . (47)
. (47)
Параметры генетического алгоритма имели следующие значения: количество возможных решений в начальной популяции 1024; число поколений 512; число попыток скрещивания в одном поколении 512; число бит для кода приращения управления 16; число бит для кода точки скрещивания 8; число бит для кода диапазона вариации 4; число вариаций в одном возможном решении 8; число поколений между сменой базисного решения 32; вероятность мутации 0,7; параметр скрещивания 0,4.
Решения искали для различных начальных значений: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Параметры фазовых ограничений имели следующие величины:
. Параметры фазовых ограничений имели следующие величины: ![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Шаг дискретизации управления составил
. Шаг дискретизации управления составил ![]() с. Время управления составляло
с. Время управления составляло ![]() с. Точность составляла
с. Точность составляла ![]() . Шаг интегрирования имел величину
. Шаг интегрирования имел величину ![]() с. Интегрирование выполнялось улучшенным методом Эйлера второго порядка.
с. Интегрирование выполнялось улучшенным методом Эйлера второго порядка.
Базисное решение задавалось в виде
![]() ,
, ![]() . (48)
. (48)
При поиске решения осуществлялся неоднократный запуск алгоритма поиска до десяти раз при различных базисных решениях, отобранных по результатам предыдущего вычислительного эксперимента.
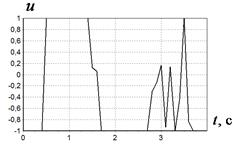
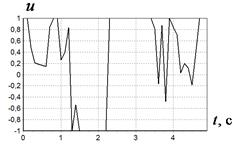
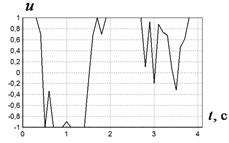
На рис. 2 приведены найденные оптимальные управления для различных начальных значений. На рис. 3 приведены графики фазовых кривых для рассматриваемых начальных значений. Там же приведены области фазовых ограничений.
Как видно из графиков, разработанный генетический алгоритм обеспечивает нахождение оптимального управления, которое удовлетворяет выполнению терминальных условий и учитывает наличие фазовых ограничений. Характер найденных оптимальных управлений имеет резкие точки перепада значений, что позволяет предположить о возможности улучшения найденных решения по значениям критериев качества.
Работа выполнена по теме гранта РФФИ № 11-08-00532-а.
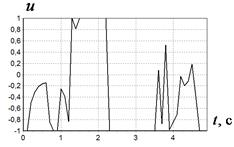
а б
в г
Рис. 2 Оптимальное управление при начальных значениях:
а:![]() ,
, ![]() ; б:
; б:![]() ,
, ![]() ; в:
; в:![]() ;
;![]() ;г:
;г:![]() ,
, ![]() .
.
а 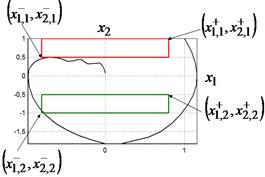 б
б 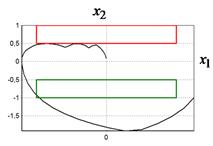
в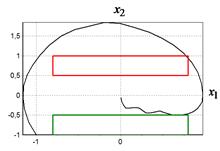 г
г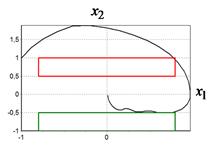
Рис. 3 Оптимальные фазовые траектории при начальных значениях:
а: ![]() ,
, ![]() ; б:
; б:![]() ,
, ![]() ; в:
; в:![]() ;
; ![]() ; г:
; г:![]() ,
, ![]() .
.
Рецензенты:
Воронин Е.А., д.т.н., профессор, заведующий кафедрой Вычислительной техники и прикладной математики Московского государственного агроинженерного университета им. В.П. Горячкина, г. Москва.
НикульчевЕ.В., д.т.н., профессор, проректор по научной работе НОУ ВПО Московский технологический институт «ВТУ», г. Москва.
Библиографическая ссылка
Дивеев А.И., Шмалько Е.Ю. ВАРИАЦИОННЫЙ ГЕНЕТИЧЕСКИЙ АЛГОРИТМ ДЛЯ РЕШЕНИЯ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ // Современные проблемы науки и образования. 2014. № 1. ;URL: https://science-education.ru/ru/article/view?id=11474 (дата обращения: 26.02.2026).



