Введение
В теории исследования поведения частиц в процессе обработки на семяочистительных машинах и сортировальных устройствах [1; 8] большое значение имеет движение самого рабочего органа. Именно оно определяет особенности движения обрабатываемого материала [2].
Нами рассматривается возвратно-колебательное движение рабочего органа конусного классификатора [7], которое создает движение частиц семенного материала по траектории в виде знака бесконечности. Исходя из сложности движения, важно исследовать в отдельности кинематику непроходовых частиц [5], остающихся на полотне решета, и проходовых частиц, просеивающихся в отверстия решет. Ускорение частиц, одна из составляющих кинематических параметров [3; 6], достаточно интенсивно меняется по времени и направлению. Поэтому мы рассмотрим вопрос о средних линейных ускорениях.
Цель работы – разработка математической модели, позволяющей проанализировать зависимость средних линейных ускорений проходовых частиц от конструктивно-установочных параметров конусного классификатора и прогнозировать их изменение для дальнейшей оптимизации процесса.
Материал и методы исследований. Исследования основывались на методах дифференциальных уравнений, математического моделирования.
В полученных дифференциальных уравнениях (1-8) учитываются следующие величины: радиусы верхнего, среднего большего, среднего меньшего, нижнего решет, основания рабочего органа (Rвр, Rсбр, Rсмр, Rнр, Rосн); расстояние между решетами (Δs); расстояние от основания каркаса до крайней левой точки решет (s1, s2, s3, s4), точки понижения; расстояние от основания каркаса до крайней правой точки решет (h1, h2, h3, h4), точки повышения; положение крайней правой точки верхнего решета при отклонении влево с верхним положением горизонтального элемента каркаса (h4лв); толщина проходовой частицы (tп); угол конуса рабочего органа классификатора (δ) [4].
Среднее линейное ускорение проходовой частицы при обработке на конусном классификаторе при отклонении влево с горизонтальным элементом в верхнем положении для верхнего (1), среднего большего (2), среднего меньшего (3), нижнего решет (4) равно:
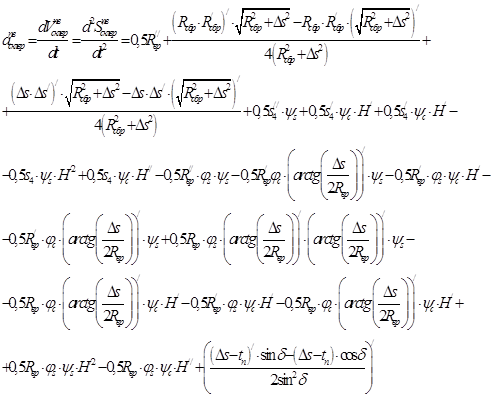 ; (1)
; (1)
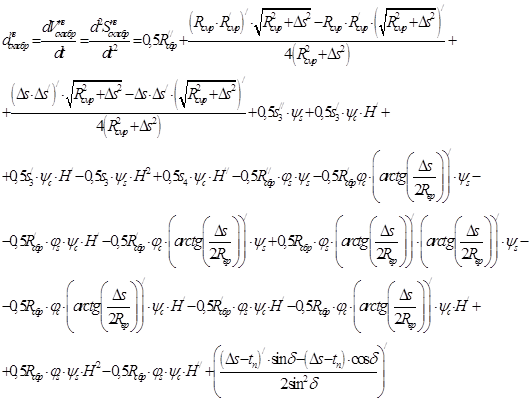 ; (2)
; (2)
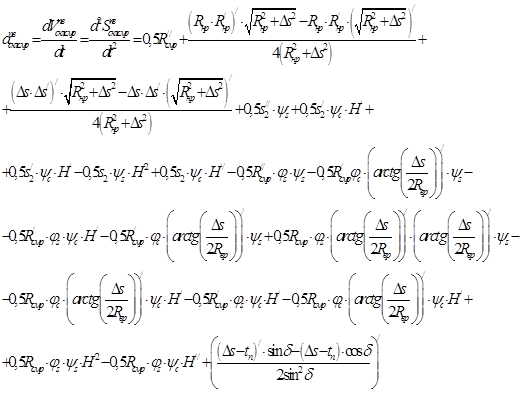 ; (3)
; (3)
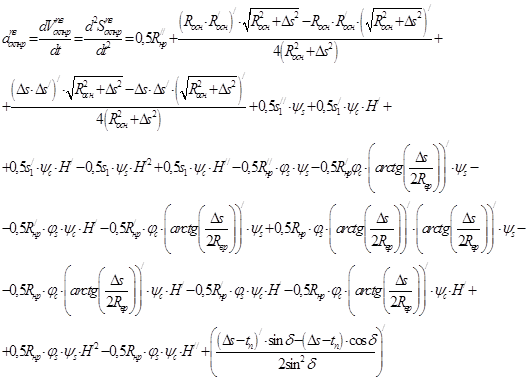 ; (4)
; (4)
где 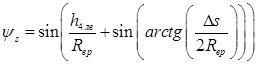 ;
; 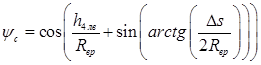 ;
;
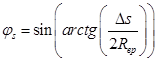 ;
; 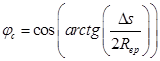 ;
; 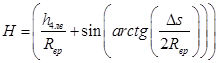 .
.
Среднее линейное ускорение проходовой частицы при обработке на конусном классификаторе при отклонении вправо с горизонтальным элементом в верхнем положении для верхнего (5), среднего большего (6), среднего меньшего (7), нижнего решет (8) равно:
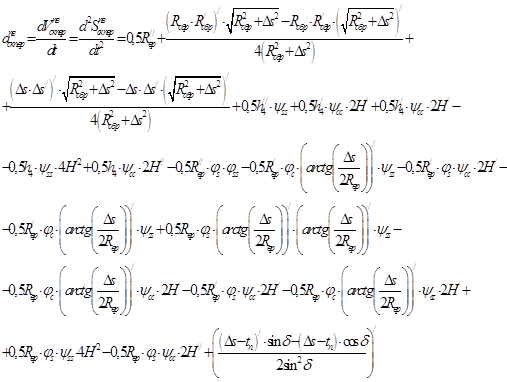 ; (5)
; (5)
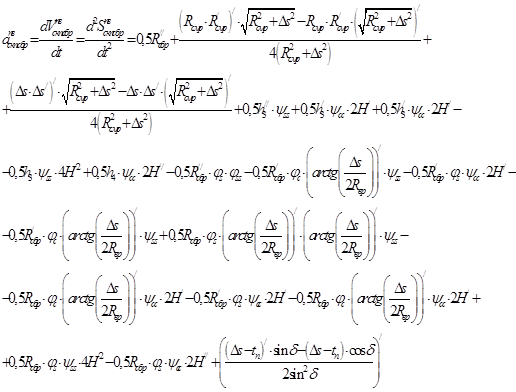 ; (6)
; (6)
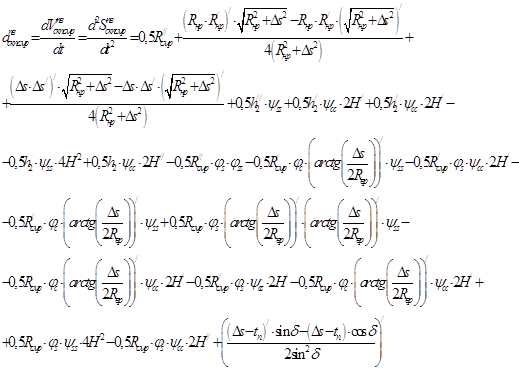 ; (7)
; (7)
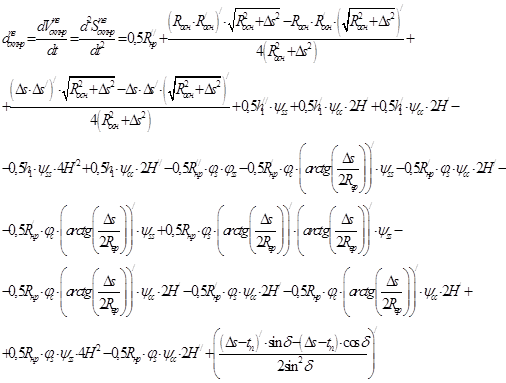 ; (8)
; (8)
где 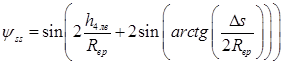 ;
;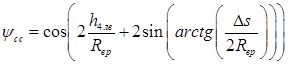 .
.
Результаты и обсуждение. Согласно дифференциальным уравнениям (1-4), средние линейные ускорения проходовых частиц при движении влево имеют линейную и квадратичную зависимости от величины радиуса соответствующего решета, от расстояния между решетами, от положения точки понижения. Дифференциальные уравнения (5-8) показывают, что средние линейные ускорения проходовых частиц при движении вправо имеют удвоенную линейную и квадратичную зависимости от величины радиуса соответствующего решета, от расстояния между решетами, от положения точки повышения. Увеличение толщины частиц обрабатываемого материала будет снижать средние линейные ускорения. А величина угла отклонения решет, определяемая положением горизонтального элемента каркаса, существенно будет изменять средние линейные скорости только при увеличении времени обработки.
Выводы
- Впервые разработана математическая модель средних линейных ускорений проходовых частиц, учитывающая движение обрабатываемого материала в виде положения крайних левых точек – точки понижения и положения крайних правых точек – точки повышения.
- Полученные дифференциальные уравнения позволяют определить влияние конструктивно-установочных параметров классификатора на кинематику семян.
- Согласно полученной математической модели оптимизировать процесс обработки семян на конусном классификаторе можно путем изменения его конструктивных особенностей.
Рецензенты:
Бартенев И.М., д.т.н., профессор кафедры «Механизация лесного хозяйства и проектирование машин» ФГБОУ ВПО «Воронежская государственная лесотехническая академия», г. Воронеж.
Попиков П.И., д.т.н., профессор, профессор кафедры «Механизация лесного хозяйства и проектирование машин» ФГБОУ ВПО «Воронежская государственная лесотехническая академия», г. Воронеж.
Библиографическая ссылка
Вахнина Г.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СРЕДНИХ ЛИНЕЙНЫХ УСКОРЕНИЙ ПРОХОДОВЫХ ЧАСТИЦ (С ВЕРХНИМ ПОЛОЖЕНИЕМ ГОРИЗОНТАЛЬНОГО ЭЛЕМЕНТА КАРКАСА) // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11306 (дата обращения: 03.03.2026).



