Введение
Построение сетей связи, предполагающих наличие различных маршрутов следования данных, опирается на знание оптимальных вариантов топологии сети, например взаимного расположения центральной станции (ЦС) (радиомодема, осуществляющего постоянную, периодическую, базовую синхронизацию всей сети) и синхрогрупп (CГ0) - совокупности потребителей, имеющих одинаковый период поступления сигнала (рис. 1) [4]. Примером наиболее распространенной сети является компьютерная сеть, работа которой определяется протоколами маршрутизации.
Протокол маршрутизации - сетевой протокол, используемый маршрутизаторами для определения возможных маршрутов следования данных в составной компьютерной сети [1]. Применение протокола маршрутизации позволяет избежать ручного ввода всех допустимых маршрутов, что, в свою очередь, снижает количество ошибок, обеспечивает согласованность действий всех маршрутизаторов в сети и облегчает труд администраторов.
Протоколы маршрутизации (в [4]) делятся на два вида, зависящие от типов алгоритмов, на которых они основаны: дистанционно-векторные протоколы (основаны на Distance Vector Algorithm (DVA)) и протоколы состояния каналов связи (основаны на Link State Algorithm (LSA)).
Также протоколы маршрутизации делятся на два вида в зависимости от сферы применения: междоменной маршрутизации и внутридоменной маршрутизации.
Цель исследования - изучение способа представления сетей маршрутизации на основе разбиения её пространства на домены.
Методы исследования базируются на математической теории групп подстановок, теории графов, теории правильных разбиений пространства. В работе использован метод конструирования модели как способ представления сети маршрутизации, дан его анализ и обобщение.
Результаты исследования и их обсуждение
В общем случае произвольной сети будем считать, что совокупность распределенных станций, связанных между собой различными способами как внутри станций, так и между ними, образует пространство сети. Система связей определяет математическую модель в виде графа [1] – графа маршрутизации сети.
Сравнительный анализ различных вариантов таких топологий, а также расчет комбинаторно возможных вариантов графа междоменной маршрутизации сетей (ГМС) позволит выделить среди них наиболее оптимальные при реализации.
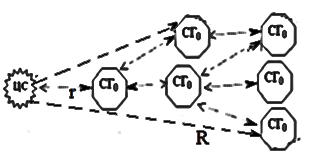
Рис. 1. Типовая схема сети с соединением «точка-точка» с синхронизацией ЦС и маршрутизацией
При классификации сетей на основе их геометрической структуры и топологии можно выделить три наиболее различающиеся между собой случая.
1. Сеть, которая сложилась стихийно. В этом случае распределение элементов сети в пространстве неоднородно и сами элементы обладают различными радиофизическими свойствами (характеристиками). Такую сеть будем называть неупорядоченной. Пример неупорядоченной сети на плоскости представлен на рис. 2. Форма доменов различна (рис. 2а), но для разработки протоколов (алгоритмов и программ) удобно выбрать аппроксимацию каждой формы с помощью полимино (рис. 2б). Это почти всегда (за исключением существования у домена только одного или двух соседей) можно сделать, не нарушая топологии сети, методом разбиения, накладывая на сеть с доменами «клеточную» решетку определенных размеров (в декартовой системе целочисленных координат).
2. Сеть создается по проекту без привязки к особенностям рельефа местности. В этом случае можно упорядочить структуру (в зависимости от различных требований), сделать, например, однородной, то есть наиболее симметричной. Для ее реализации относительно легко разработать стандарт и выбрать оптимальное устройство. Будем называть эту сеть полностью или глобально упорядоченной. Геометрическим примером такой сети является правильная решетка трансляций (узлов с «пустыми» ячейками).
3. Третий вариант представляет собой сочетание локально неупорядоченной структуры с глобальной упорядоченностью. В качестве основного объекта исследования в данной работе выберем именно такой вариант сети: решетка трансляций с фундаментальной областью, заполненной неупорядоченными доменами. Сеть в этом случае назовем локально неупорядоченной.
Любой промежуточный вариант перехода от упорядоченной структуры сети к неупорядоченной сети будет характеризоваться наличием случайных «дефектов» и относиться к разряду дефектных сетей. Устойчивая работа сети часто определяется радиационной защищенностью отдельных элементов радиотехнических устройств, особенно при их миниатюризации. Наши исследования показали, что на микро- и наноуровне радиация приводит к перестройке нанокластеров и изменению функциональных свойств «квантовых точек». Точное количество дефектных сетей, в общем случае, непредсказуемо. Тем не менее в каждом конкретном случае введением вероятностных закономерностей можно получить результат распространения сигналов по сети при наличии дефектов.
Ниже рассмотрим геометрическую модель 3 для описания работы локально неупорядоченной сети. Произведем разбиение пространства сети на домены СГ0 . Так как в математике нет общего алгоритма разбиения пространства на домены с различной внутренней конфигурацией, воспользуемся структурным упрощением, заключающемся в таком расположении синхрогрупп (СГ0), каждая из которых способна выполнять функцию центральной, и в этом случае все домены группы функционально равноправны, но при этом могут иметь разное количество связей. Ограничения, накладываемые на «длину связи», максимальный радиус действия которой R, приводят к модели (r-R) – системы Делоне [1], пример которой изображен на рис. 2в, и ее представление в виде доменов Дирихле (рис. 2г).
Каждому элементу сети маршрутизации (участнику процесса передачи-получения сигнала) на евклидовой плоскости ставится в соответствие некоторая область, назовем её доменом (областью Дирихле), необходимая для задания дискретной плоскости (пространства), которая представляет собой результат нормального разбиения непрерывной плоскости (пространства) на одинаковые многоугольники (в трехмерном случае -многогранники). Зададим порядок разбиения количеством вершин планигонов, попавших в элемент произвольной области, построенной на этих вершинах, затем присвоим каждому порядковый номер, условно полагая, что в вершинах находятся «потребители сигнала» и выделим для каждого потребителя клетку-домен Дирихле. Таким образом, получим разбиение плоскости на домены Дирихле.
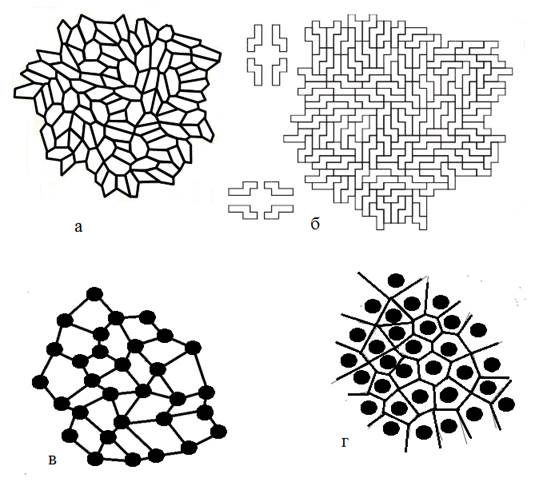
Рис. 2. Неупорядоченные сети. Топология графа сетей (а) и (б) одинакова. Система точек Делоне (в) и домены Дирихле (г) системы точек Делоне.
Для геометрического описания отношения соседства используем граф соседства. Поскольку распространение сигнала по сети представляет собой направленный процесс, то граф отношения соседства будет ориентированным, а модель передачи возмущения (сигнала) может быть описана с помощью растущего по определенным правилам графа маршрутизации сети, который построен на множестве условно выбранных точек (устройств) – центров доменов разбиения (рис. 2а). Совокупность одинаковых СГ0 - доменов или их комбинации могут располагаться в пространстве маршрутизаций сети различным способом, образуя систему разбиения всего пространства. Существование общей границы между областями, в разбиении на области (рис. 2б), определяет отношение соседства, заданного ребром графа. Требования конечности расстояний между ними приводит либо к разбиению, либо к плотной «упаковке» доменов в локально неупорядоченном варианте, что можно представить для наглядности следующим образом (рис. 3).
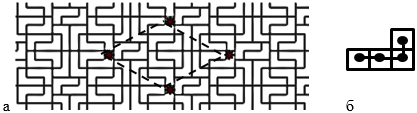
Рис. 3. Пример локально неупорядоченного разбиения пространства маршрутизации сети на домены (а) с выделенной фундаментальной областью. Домен - полимино и его внутренняя конфигурация (б).
Алгоритм и программа построения разбиения будут обсуждены в отдельной работе. Очевидно, что результат междоменной маршрутизации зависит от формы отдельных доменов, участвующих в разбиении. Количество вариантов полимино с заданным числом клеток, образующих его, в общем случае, в математике неизвестно. В данном исследовании рассмотрим основную часть задачи перечисления конкретных (частных) форм доменов-полимино. Определим количество конфигураций деревьев внутридоменного графа точек- центров клеток полимино.
Внутренняя организация доменов определяет возможность существования контактов между синхрогруппами при маршрутизации, т.е. говорит о способности построения связи между элементами сети. Конфигурацию каждой СГ0 следует считать заданной, если имеется информация о полном наборе степеней вершин соответствующего графа, не учитывая последовательности их расстановки. В теории графов [1] имеется теорема о зависимости числа вершин от числа ребер.
Теорема 1. Сумма степеней n вершин графа равна удвоенному числу его ребер 2(n-1).
В случае дерева графа, определяющего различные типы полимино (или n-мино, где n - количество клеток в полимино, имеющих хотя бы одну общую сторону), возможными являются степени вершин от 1 до 4, как это представлено на рис. 2б для каждого домена. Введем обозначения количества вершин графа степени 1 через x1, степени 2 – x2, степени 3 – x3, степени 4– x4. Тогда, учитывая положение теоремы 1 и представление о данном графе, составим следующую систему уравнений (1):
![]() (1)
(1)
где x1, … ,x4 – принадлежат множеству целых чисел, ![]() , n – количество вершин графа, в квадратных скобках обозначена целая часть числа.
, n – количество вершин графа, в квадратных скобках обозначена целая часть числа.
Для удобства расчетов из уравнений системы (1) могут быть составлены еще три уравнения, однако линейно независимыми по-прежнему останутся только два. Составим новую систему (2) для выполнения конкретных расчетов:
 (2)
(2)
Используя эти условия, рассчитаем числа xi для полимино с n = 8 квадратами. Значение x4max=2, комбинаторный перебор целых чисел x1 и x3 выполняем, учитывая соотношение третьего уравнения системы (2) при x4=2,1,0. Затем при определенных значениях x1, x3, x4 вычисляем x2 из первого уравнения системы (2). Наборы решений занесем в табл. 1.
Таблица 1. Наборы конфигураций деревьев графа, характеризующего внутридоменную структуру, при n=8
|
xi |
Номера конфигураций графа |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
x4 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
|
x3 |
0 |
1 |
0 |
3 |
2 |
1 |
0 |
|
x2 |
0 |
1 |
3 |
0 |
2 |
4 |
6 |
|
x1 |
6 |
5 |
4 |
5 |
4 |
3 |
2 |
Полный перебор различных наборов xi показал, что их число оказалось равным K(n)=7 .
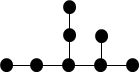
Для того чтобы пересчитать различные варианты конфигураций деревьев графа, определяющего внутреннюю структуру домена, необходимо учесть порядок следования вершин в графе. В качестве примера рассмотрим варианты для набора 5 из табл. 1, где x4=0, x3=2, x2=2, x1=4. Данный набор степеней вершин показывает, что в варианте конфигурации нет вершин степени 4, вершин степени 2 и 3 – две и четыре вершины, имеющие степень 1 (концевые).
Таким образом, для заданной конфигурации (x4=0, x3=2, x2=2, x1=4), характеризующей внутреннюю организацию домена (СГ0), имеется всего пять структурно независимых вариантов, интерпретация которых в виде деревьев графа представлена на рис. 4.
![]()
![]()
![]()
![]()
Рис. 4. Варианты внутридоменных структур СГ0 с x4=0, x3=2, x2=2, x1=4.
Компьютерный расчет числа наборов конфигураций в общем случае, для произвольного n, дается в работе [4] и приводит к следующему графику зависимости K(n) (рис. 5).
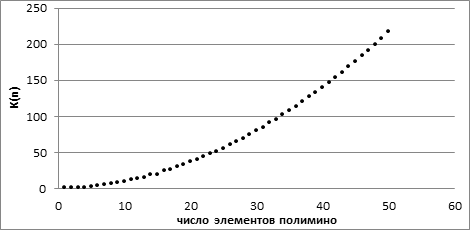
Рис. 5. График зависимости количества Кn от числа элементов полимино
Опуская детали доказательства, сформулируем общий результат в виде теоремы 2.
Теорема 2. Количество Kn – различных наборов конфигураций деревьев графа доменов-полимино с n – числом вершин находится по формуле
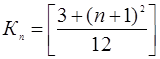 ,
,
где квадратные скобки обозначают целую часть заключенного в них числа. Вывод формулы основывается на анализе результатов, полученных нами ранее в работе [4].
Как сказано выше, совокупность одинаковых СГ0 - доменов или их комбинации могут располагаться в пространстве маршрутизаций сети различным способом. Кроме этого, в разбиении могут участвовать домены с различной конфигурацией, например так, как это показано на рис. 6. Все это значительно увеличивает возможности проектирования вариантов маршрутизаций сетей.
а б
б 
Рис. 6. Разбиение области пространства сети на три варианта доменов (а) с различной конфигурацией (б).
Выводы
Таким образом, введение пространства маршрутизации сети, его разбиение на домены синхрогруппы и перечисление конфигураций деревьев внутридоменного графа позволяет перейти к следующей задаче – полному представлению вариантов локально-неупорядоченных сетей междоменной маршрутизации с помощью компьютерной автоматизации проектирования, что будет сделано в следующей статье.
Рецензенты:
Поздняков А.Д., д.т.н., профессор ФГБОУ ВПО «Владимирский государственный университет имени А.Г. и Н.Г. Столетовых», г. Владимир.
Полушин П.А., д.т.н., профессор ФГБОУ ВПО «Владимирский государственный университет имени А.Г. и Н.Г. Столетовых», г. Владимир.
Библиографическая ссылка
Горшков К.А., Никитин О.Р., Рау Т.Ф., Али Аббас Мохсин Али, Рау В.Г. КОМБИНАТОРНО-ГЕОМЕТРИЧЕСКИЙ МЕТОД РАСЧЕТА И ПРЕДСТАВЛЕНИЯ ВАРИАНТОВ КОНФИГУРАЦИЙ ДЕРЕВА ГРАФА СЕТЕВЫХ ДОМЕНОВ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11297 (дата обращения: 13.02.2026).



