Введение
Решение задач экономического подъема страны тесно связано с выработкой эффективных механизмов управления стратегией развития регионов, координацией различных направлений экономической политики региональных властей, взаимодействия региональных производственного, социального и бюджетно-финансового секторов. В связи с переходом на рыночные методы хозяйствования в РФ, перед каждым экономическим агентом (ЭА) в регионе возникает необходимость принимать экономически и социально обоснованные управленческие решения при выборе из множества возможных альтернатив развития. Сделать оптимальный выбор чрезвычайно трудно без использования системного подхода, который должен включать разработку математических моделей региона [3], аналитического и алгоритмического инструментария их анализа и создания автоматизированных систем поддержки принятия управленческих решений на языке, понятном профессионалу, экономисту-практику, аналитику [4, 5]. Следует отметить при этом, что анализ и синтез моделей управления экономическими системами, в частности, мезоуровня, неизбежно требует учета различных аспектов инновационного производства.
В существующих же пакетах экономического и финансового анализа (ИНЭК–Аналитик, Альт–Инвест, Галактика, Project Expert и др.) на сегодняшний день отсутствуют возможности оценки эффективности инвестиционных проектов (ИП) с использованием методов теории оптимального управления. Между тем без использования указанных методов затруднительно определить оптимальный баланс в развитии региональной социально-экономической системы и всех ее подсистем. В работе [6] предложена статическая многокритериальная модель региона, учитывающая взаимодействие пяти ЭА. К недостаткам указанной модели относится изначальная несимметричность в описании взаимодействия ЭА с точки зрения распределения денежной массы в экономической системе, а также такого ресурса, как дотации управляющего органа остальным ЭА. Указанные недостатки устраняются в данной работе.
Содержательная постановка задачи
Рассмотрим следующую задачу эффективного экономического развития региона. Пусть в регионе функционируют и взаимодействуют пять экономических агентов: производитель (Р), потребитель (С), финансовый сектор (F), коммерческий (торговый) сектор (Соm), региональный управляющий (налоговый) центр (Т). Инвестор имеет начальный капитал (свободные денежные средства). У него существует возможность организовать производство n видов продукции (в том числе инновационной), инвестировав в деятельность (Р). В свою очередь, (Р) может купить, арендовать активные ОПФ – станки, оборудование, оргтехнику, ОПФ производственных предприятий отдельной отрасли, ОПФ n производственных подразделений или направлений экономической деятельности и т.п. (С) получает от (Р) средства к существованию (заработная плата) и тратит их на свою потребительскую корзину (consumer basket (СВ)). (Com) приобретает оптом произведенную (Р) продукцию и организует торговлю ею. (F) аккумулирует в виде депозитов временно свободные денежные средства других ЭА и выдает их в виде кредитов. (Т) организует взаимодействие ЭА путем взимания налогов и перераспределения финансового ресурса в виде дотаций другим экономическим агентам. Требуется определить оптимальное количество приобретаемых единиц ОПФ, объемы выпуска и выручку от продажи продукции каждого вида, объемы дотаций, кредитов и депозитов, при которых дисконтированное сальдо доходов и расходов (Р), (С), (F), (Соm), а также дисконтированный налоговый поток (Т) за горизонт планирования T являются максимальными с учетом интересов и естественных ограничений деятельности каждого экономического агента.
Математическая постановка задачи
Введем следующие обозначения: ck – стоимость ОПФ k-го типа (руб), k=1,…,n; mk – количество приобретаемых ОПФ k-го типа (ед); Vk – проектная производительность ОПФ k-го типа (руб); Pk – стоимость единицы продукции k-го типа (руб); ![]() – фондоотдача ОПФ (руб); yk – объем выпуска по
– фондоотдача ОПФ (руб); yk – объем выпуска по ![]() -ому виду продукции (ед); qk – прогнозный спрос на продукцию k-го типа (руб); R – выручка от реализации всей производимой продукции (руб); Zr – общие затраты производителя (руб);
-ому виду продукции (ед); qk – прогнозный спрос на продукцию k-го типа (руб); R – выручка от реализации всей производимой продукции (руб); Zr – общие затраты производителя (руб); ![]() – амортизационные отчисления (руб); Wb– балансовая прибыль производителя (руб);
– амортизационные отчисления (руб); Wb– балансовая прибыль производителя (руб); ![]() – чистая прибыль производителя (руб); С0 – начальные средства потребителя (руб);
– чистая прибыль производителя (руб); С0 – начальные средства потребителя (руб); ![]() – начальные средства финансового сектора (руб); Com0 – начальные средства коммерческого сектора (руб);
– начальные средства финансового сектора (руб); Com0 – начальные средства коммерческого сектора (руб); ![]() – максимальная сумма внешних инвестиций (руб);
– максимальная сумма внешних инвестиций (руб); ![]() – максимальная сумма дотаций за весь период действия ИП (руб); rps(k) – экспертно задаваемый коэффициент, отражающий, во сколько раз выручка на стадии послепродажного сервиса больше выручки от продаж k-го вида продукции; N1, N2, N3, N4 – налоги на добавленную стоимость (НДС), на имущество (НИ), на прибыль (НП) и страховые взносы (СВ) (руб); α1, α2, α3, α4 – соответствующие ставки налогов (%); Cr1, Cr2, Cr3, Cr4 – кредиты (F) для (Р), (С), (Com) и (T); ε1, ε2, ε3, ε4 – соответствующие средние ставки кредитов (%); Dep1, Dep2, Dep3, Dep4 – депозиты (F) для (Р), (С), (Com) и (T); η1, η2, η3, η4 – соответствующие средние ставки депозитов (%); Dot1, Dot2, Dot3, Dot4 – дотации (T) для (Р), (С), (Com) и (F); ξ1, ξ2, ξ3, ξ4 – соответствующий процент возврата дотаций (%); Zcom – затраты торговли (транспорт, магазины и пр.), I – внешние для региона займы под процент i; β – доля прибыли, поступающая в фонд оплаты труда (%); δ – торговая надбавка коммерческого сектора (%); p – доля оборотных затрат в общих затратах производителя (%); κ – доля собственных средств (F), выделяемая на кредиты (%); λ – доля собственных средств (F), выделяемая на депозиты;
– максимальная сумма дотаций за весь период действия ИП (руб); rps(k) – экспертно задаваемый коэффициент, отражающий, во сколько раз выручка на стадии послепродажного сервиса больше выручки от продаж k-го вида продукции; N1, N2, N3, N4 – налоги на добавленную стоимость (НДС), на имущество (НИ), на прибыль (НП) и страховые взносы (СВ) (руб); α1, α2, α3, α4 – соответствующие ставки налогов (%); Cr1, Cr2, Cr3, Cr4 – кредиты (F) для (Р), (С), (Com) и (T); ε1, ε2, ε3, ε4 – соответствующие средние ставки кредитов (%); Dep1, Dep2, Dep3, Dep4 – депозиты (F) для (Р), (С), (Com) и (T); η1, η2, η3, η4 – соответствующие средние ставки депозитов (%); Dot1, Dot2, Dot3, Dot4 – дотации (T) для (Р), (С), (Com) и (F); ξ1, ξ2, ξ3, ξ4 – соответствующий процент возврата дотаций (%); Zcom – затраты торговли (транспорт, магазины и пр.), I – внешние для региона займы под процент i; β – доля прибыли, поступающая в фонд оплаты труда (%); δ – торговая надбавка коммерческого сектора (%); p – доля оборотных затрат в общих затратах производителя (%); κ – доля собственных средств (F), выделяемая на кредиты (%); λ – доля собственных средств (F), выделяемая на депозиты; ![]() – ставка дисконтирования (средняя доходность проекта) (%).
– ставка дисконтирования (средняя доходность проекта) (%).
Балансовые уравнения суммы собственных средств ЭА имеют вид:
(Р): ![]() ,
,
(С): ![]()
![]() ,
,
(F): ![]() ,
,
(Com): ![]() ,
,
(T): ![]() .
.
Ограничения деятельности экономических агентов региона
Предположим, в первую очередь, платежеспособность производителя, потребителя, коммерческого и финансового сектора: DP≥0, DC≥0, DCom≥0, DF≥0.
Условия ограниченности сумм инвестиций и дотаций можно записать следующим образом:
(Р): ![]() , (1)
, (1)
(T): ![]() , (2)
, (2)
(F): ![]() , (С):
, (С): ![]() . (3)
. (3)
Условие (1) ограничивает максимальные суммы инвестиций (P), а (2) – максимальные суммы дотаций агента (Т) агентам (Р), (С), (Com) и (F). Условия (3) ограничивают суммы кредитов и депозитов для ЭА заданными частями его собственных средств. По смыслу рассматриваемой задачи имеем следующие ограничения: ![]() ,
, ![]() , означающие, соответственно, что выпуск продукции k-го типа не превосходит производительности ОПФ, а объем продаж не превышает спроса.
, означающие, соответственно, что выпуск продукции k-го типа не превосходит производительности ОПФ, а объем продаж не превышает спроса.
В качестве критериев эффективности функционирования ЭА рассмотрим следующие показатели:
(Р): ![]() ,
,
(С): ![]() ,
,
(F): 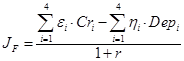 ,
,
(Com): ![]() ,
,
(T):![]() .
.
Следует отметить, что перечисленные показатели качества функционирования отражают не все потоки собственных средств ЭА, а только потоки стратегического (долгосрочного) характера, проявляющиеся на всем горизонте планирования регионального проекта развития. В частности, в целевые критерии не включаются потоки кредитной и депозитной денежной массы и потоки дотаций.
Введем далее следующие переменные:
![]() – общая стоимость ОПФ k-го типа;
– общая стоимость ОПФ k-го типа; ![]() – выручка от реализации продукции k-го типа;
– выручка от реализации продукции k-го типа;
|
x2n+1 = Dot1 x2n+2 = Dot2 x2n+3 = Dot3 x2n+4 = Dot4 |
x2n+5 = Cr1 x2n+6 = Cr2 x2n+7 = Cr3 x2n+8 = Cr4 |
x2n+9 = Dep1 x2n+10 = Dep2 x2n+11 = Dep3 x2n+12 = Dep4 |
|
x2n+13=Zcom x2n+14= I |
||
Обозначим далее ![]() – сумма амортизационных отчислений по всем видам ОПФ;
– сумма амортизационных отчислений по всем видам ОПФ; ![]() – выручка от продажи по всем видам продукции;
– выручка от продажи по всем видам продукции; ![]() – остаточная стоимость ОПФ;
– остаточная стоимость ОПФ; ![]() – налог на имущество,
– налог на имущество, ![]() – срок действия ИП; чистая прибыль (P) может быть рассчитана по формуле
– срок действия ИП; чистая прибыль (P) может быть рассчитана по формуле ![]() .
.
Заметим, что технико-экономические характеристики и производственная функция (Р) вычисляются алгоритмически в соответствии с принятыми в РФ правилами учета затрат.
С учетом введенных обозначений, математическая модель решаемой задачи примет вид:
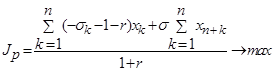 , (4)
, (4)
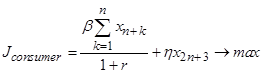 , (5)
, (5)
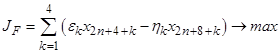 , (6)
, (6)
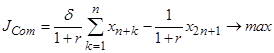 , (7)
, (7)
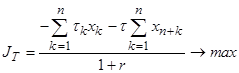 . (8)
. (8)
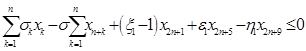 , (9)
, (9)
![]() , (10)
, (10)
![]() , (11)
, (11)
![]() , (12)
, (12)
![]()
![]() , (13)
, (13)
![]() , (14)
, (14)
![]() , (15)
, (15)
![]() , (16)
, (16)
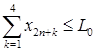 , (17)
, (17)
![]() , (18)
, (18)
![]() , (19)
, (19)
![]() , (20)
, (20)
где 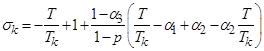 ,
, ![]() ,
,
![]() ,
, ![]() .
.
Построенная модель (4)-(20) является многокритериальной задачей линейного программирования, допускающей решение на основе симплекс-метода. Многокритериальный анализ проводится путем перехода к эквивалентной однокритериальной задаче с выпуклой линейной комбинацией критериев [8] с последующим возвращением к многокритериальности и построения множества Парето.
В моделе учтены существенные ограничения деятельности ЭА, не позволяющие системе работать в кризисных режимах. В частности, обеспечиваются условия платежеспособности (9)-(13) всех ЭА, устанавливаются ограничения (14) выпуска продукции спросом на нее, исключающие кризис перепроизводства продукции. Кроме того, (15) можно трактовать как ограничения на эффективности ОПФ или уровень научно-технического прогресса. В условиях (14), (15), кроме того, учтен эффект увеличения выручки от продажи продукции на стадии послепродажного обслуживания, которая характерна для инновационной продукции.
Условия (16), (17) содержат ограничения на объемы циркулирующих в системе финансовых ресурсов (инвестиции и дотации), а условия (18), (19) ограничивают объемы кредитно-депозитной массы, что, как представляется, позволит избежать перепроизводства финансового ресурса в системе (финансовых пузырей). Приведенная модель является обобщением на случай пяти ЭА моделей региона, рассмотренных в работе [2]. Особенностью указанной модели является ее линейный и статический характер, что позволяет разрабатывать эффективные алгоритмы ее численного анализа, а также создавать автоматизированные пакеты прикладных программ (ППП), нацеленные на поддержку принятия управленческих решений по разработке различных направлений экономической политики региональных властей. Примером такого ППП может служить программный комплекс [1, 7]. Предварительные расчеты, проведенные с его помощью, позволили сделать вывод о существовании решения поставленной задачи.
Обсуждение подхода и алгоритмы анализа задачи
Предлагаемый в работе подход занимает промежуточное положение между излишне агрегированными (использующими отвлеченные производственные функции) и излишне детализированными (используемыми, как правило, для имитационного описания систем) аналогами и позволяет достичь разумного компромисса в соотношении уровня сложности и содержательной адекватности описания региональных экономических процессов. При этом научно обоснованный прогноз и планирование наилучших параметров развития региона осуществляется на основе многокритериального выбора с учетом интересов основных экономических агентов региона – производственного, потребительского, финансового, коммерческого секторов и регионального управляющего центра.
Рассмотрим примерный алгоритм использования СППР при разработке выбранных направлений экономической деятельности региона. Данный алгоритм, как правило, содержит следующие этапы.
1. Сбор статистической информации о показателях экономического развития отраслей в регионах (средние значения сроков службы, производительности и стоимости активов, стоимости единицы производимой продукции, средние по отраслям затраты на оборотные средства, оплату труда, ставки налогов, средние ставки кредитов, затраты коммерческого сектора, стоимость потребительской корзины).
2. Проведение маркетингового исследования рынка продукции отраслей региональной экономики с целью определения спроса на продукцию и рыночных характеристик ОПФ как внутри региона, так и за его пределами. Если проведение такого исследования невозможно или затратно, то предполагается параметрический анализ модели по параметрам спроса.
3. Выбор параметров модели, соответствующей статистическим данным (с учетом количества участников, горизонта планирования, видов производимой продукции, полноты собранной статистической информации и т.п.). Проведение численных расчетов при заданных характеристиках рассматриваемого регионального проекта развития.
3.1) если чистая приведенная стоимость собственных средств хотя бы одного экономического агента равна нулю, то данный проект классифицируется как неокупаемый или кризисный для данного экономического агента.
3.2) в случае положительных значений критериев всех ЭА требуется более глубокое исследование с точки зрения устойчивости проекта к изменению его параметров.
4. Сравнение результатов проведенного расчета в качественном и количественном аспекте со сложившимися в данном регионе по данному направлению экономической деятельности показателями (накопленная стоимость, стоимость приобретаемых или планируемых к приобретению ОПФ, выручка от реализации продукции, остаточная стоимость накопленных ОПФ, внешние и внутренние инвестиции, их накопленные суммы, объемы кредитной массы и т.п.).
4.1) если полученные численные данные близки к реально сложившимся, а также устраивают всех участников регионального проекта (удовлетворяют их требованиям эффективности проекта), то можно сделать вывод о сбалансированности социально-экономического развития региона в смысле интересов всех его экономических агентов;
4.2) если полученные численные данные не совпадают с реально сложившимися экономическими показателями или значения целевых критериев не устраивают одного или нескольких принимающих решения лиц (ЛПР), то можно сделать вывод о несбалансированном (ассиметричном, кризисном) развитии региона и выбрать в качестве ориентировочных пропорций показатели произведенного расчета. При этом на основе критериальных Парето-множеств ЭА или ЛПР имеют возможность согласования своего взаимодействия в рассматриваемом проекте, например, путем уступок своих интересов.
В случае если расчетные данные указывают на неэффективность проекта, с помощью автоматизированного пакета программ [1] возможно проведение численного эксперимента для нахождения диапазонов изменения параметров и их комплексов, улучшающих региональный проект по критериям. При определенных условиях может оказаться целесообразным получить такие характеристики регионального проекта, которые удовлетворяли бы интересам не всех участников, а лишь некоторых, приоритетных экономических агентов региона.
Заключение
Построенная в работе математическая модель, методы ее численного анализа в виде пакета прикладных программ, способов алгоритмизации введения входной и обработки выходной информации, выработка законодательных актов по установлению налоговых ставок, определению сумм и ключевых направлений дотаций, ставок и объемов кредитов для каждого экономического агента, размеров доходов потребителя и его потребительской корзины, а также принятие других управленческих решений на основе получаемой из приведенной модели информации могут представлять собой научно обоснованную систему (механизм) и повысить обоснованность принятия решений при управлении региональным социально-экономическим развитием.
Рецензенты:
Кучер Н.А., д.ф.-м.н., профессор, зав. кафедрой дифференциальных уравнений ФГБОУ ВПО «Кемеровский государственный университет», г. Кемерово.
Никитенко С.М., д.э.н., доцент, директор ООО ИНПЦ «Иннотех», г. Кемерово.
Библиографическая ссылка
Медведев А.В., Смольянинов А.В., Аврова Л.С., Колесникова Е.Г. АНАЛИЗ ЭКОНОМИКИ РЕГИОНА НА ОСНОВЕ МНОГОКРИТЕРИАЛЬНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11290 (дата обращения: 13.02.2026).



