Введение. Корректирование режимов технического обслуживания заключается в уточнении перечня операций технического обслуживания и периодичности их выполнения с целью достижения режимов, оптимальных для данных условий эксплуатации.
Под оптимальным режимом технического обслуживания автомобиля понимается периодичность и перечень выполняемых операций, при которых обеспечивается не только требуемая надежность автомобиля в эксплуатации, но и минимальные затраты на техническое обслуживание и ремонт автомобиля, приходящиеся на единицу пробега или транспортной работы. В связи с этим при корректировании режимов необходимо совместно рассматривать как удельные приведенные затраты на техническое обслуживание и ремонт автомобилей, так и показатели надёжности. Следовательно, рассматриваемая задача состоит в определении численных значений перечня операций технического обслуживания (ТО) и периодичности их обслуживания, при которых обеспечивается заданный при минимальных затратах на техническое обслуживание и ремонт автомобилей. Решение этой задачи удобно производить с помощью методов математического моделирования. Для этого строится математическая модель зависимостей суммарных удельных приведенных затрат на техническое обслуживание и ремонт от величин периодичностей и перечней операций ТО [1,2,4].
С помощью построенной модели отыскиваются значения периодичностей и перечней, при которых указанные затраты минимальны.
К узлам и системам автомобиля предъявляются определенные требования к показателям надежности. Эти показатели зависят от многих факторов, в том числе от режимов ТО. Поэтому при расчете режимов необходимо совместно учитывать не только затраты, но и показатели надежности [5].
Теоретический анализ. Требования к показателям надежности можно представить в виде ограничений, накладываемых на критерий оптимизации. В этом случае задачу уточнения перечня операции ТО и периодичности их выполнения можно сформулировать следующим образом:
определить значения 
и 
, при которых
,
при условии
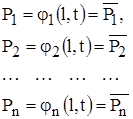(1)
где 
- соответственно оптимальные периодичности и объем работ технического обслуживания;
- суммарные удельные приведенные затраты на ТО и ремонт автомобилей;
- показатели надежности, подлежащие учету при корректировании периодичности и объема работ;
- зависимости показателей надежности от режимов ТО;
- нормативные значения показателей надежности, которые нужно обеспечить при корректировании режимов ТО.
Практическое использование целевой функции (1) представляет собой большую трудность вследствие того, что величина одновременно зависит как от периодичности, так и от объема работ, то есть является функцией двух переменных, которые в свою очередь находятся в сложной зависимости.
Задача усложняется тем, что автомобиль в целом является сложной технической системой, состоящей из множества подсистем и элементов. Требования к надежности различных подсистем и элементов неодинаковы, различны также показатели надежности, которые целесообразно учитывать при определении оптимальных режимов [6-7].
Методика. Для упрощения задачи целесообразно ее решение осуществлять в два этапа. Вначале определить оптимальную периодичность выполнения операций ТО, принимая при этом постоянный перечень. Затем произвести уточнение перечня операций ТО при оптимальной периодичности.
При уточнении периодичности выполнения операций ТО целесообразно рассматривать те элементы автомобиля, периодичность обслуживания которых оказывает существенное влияние на удельные затраты и показатели надежности. Эти элементы имеют различную конструкцию, работают в неодинаковых условиях, требуют выполнения различных по характеру операций обслуживания и разной периодичности. Следовательно, они не образуют однородных групп и установление для них единой периодичности нецелесообразно.
Поэтому необходимо из ряда деталей, узлов и механизмов, существенно влияющих на принятый критерий оптимизации, выделить качественно однородные группы и сформулировать задачу оптимизации для каждой группы.
При составлении классификации выбор признака группировки элементов автомобиля зависит от поставленных задач. В данном случае при выделении совокупностей целесообразно учитывать виды операций технического обслуживания, сходство условий работы элементов, требования, предъявляемые к показателям надёжности и функциональным показателям элементов [10].
По виду операций технического обслуживания элементы группируются на элементы, требующие осмотровых и диагностических крепежных, регулировочных и смазочных работ. По сходству условий работы элементы автомобиля группируются на элементы, работающие в условиях трения, испытывающие закономерные нагрузки, испытывающие высокое давление и т.д.
При группировке элементов в зависимости от показателей надёжности и функциональных показателей необходимо учитывать требования к функциональным показателям и показателям надёжности элементов. Целесообразно при этом выделить группу элементов, обеспечивающих безопасность движения, к которым предъявляются повышенные требования и отношения надёжности [8-9].
Для каждой группы однородных элементов задача корректирования периодичности ТО в общем виде формулируется следующим образом:
,
при условии
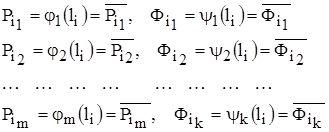(2)
где 
- оптимальная периодичность операций ТО одной группы элементов;
- суммарные удельные приведенные затраты на ТО и ремонт однородной группы элементов;
- показатели надёжности элементов, подлежащие учету при определении периодичности;
- нормативные значения показателей элементов, подлежащих учету;
- показатели функциональных свойств элементов, которые необходимо учитывать при определении периодичности;
- нормативные значения показателей функциональных свойств элементов;
- зависимость показателей надёжности элементов от периодичности ТО;
- зависимость показателей функциональных свойств от периодичности ТО.
Задача определения рационального перечня операций ТО формулируется аналогично. Ее отличие состоит в том, что зависимости удельных затрат, показателей надежности и показателей функциональных свойств от перечня операций ТО будут непрерывными и дискретными.
Характерной чертой зависимостей, входящих в целевую функцию (2), является то, что и зависимые, и независимые переменные являются величинами случайными, так как они зависят от большого числа случайных факторов. Подобные зависимости носят название корреляционных. Для их описания применяются математические модели, описывающие усредненный закон изменения зависимой переменной от независимой [9-10].
Накопленная к настоящему времени информация позволяет теоретически установить форму связи между переменными, входящими в модели целевой функции (2) и выбрать целесообразную структуру и вид моделей, описывающих эту связь.
В частности, зависимость суммарных удельных затрат на техническое обслуживание и ремонт автомобиля от периодичности обслуживания имеет вид параболы. Это обусловлено тем, что при увеличении периодичности будет увеличиваться стоимость ремонта, в то время как затраты на обслуживание будут снижаться [1-3]. Учитывая форму связи между суммарными затратами и периодичностью обслуживания, для аналитического описания зависимости критерия оптимизации от периодичности обслуживания можно воспользоваться зависимостью следующего вида:
. (3)
Изменение показателей надежности и показателей функциональных свойств элементов обусловлено износом деталей. При увеличении периодичности обслуживания износ увеличивается. Это изменение носит направленный характер в сторону увеличения. Следовательно, показатели надёжности и показатели функциональных свойств при изменении периодичности будут изменяться монотонно и иметь одну точку перегиба. Для аппроксимации этих зависимостей можно использовать полином второй степени. Поэтому рассматриваемые модели зависимостей будут иметь следующий вид
, 
. (4)
где 
- коэффициенты полинома.
Таким образом, целевая функции (2) будет иметь следующий вид
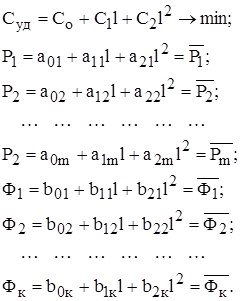(5)
Математические модели, входящие в целевую функцию (5) описывают связь между случайными величинами. Для построения подобных моделей используются методы корреляционного регрессионного анализа. Они заключаются в вычислении корреляционного отношения для рассматриваемых зависимостей, проверке их существенности, нахождении коэффициентов регрессии и оценки их значимости, определении остаточной дисперсии и сравнении ее с дисперсией величины принятого критерия.
Эффективность применения методов корреляционного и регрессионного анализа определяется объёмом и видом информации, получаемой при экспериментальных исследованиях, и степенью ее достоверности.
Вывод. В случае адекватности уравнений построенная целевая функция используется для расчёта оптимальной периодичности. Если условие адекватности не соблюдается, то в многочлены вводятся добавочные члены, после чего вновь рассчитываются коэффициенты регрессии и определяется адекватность уточненной модели. Этот процесс последовательно повторяется до тех пор, пока не будут получены модели, удовлетворяющие условию адекватности.
Рецензенты:
Скрыпников А.В., д.т.н., профессор, профессор кафедры информационные технологии моделирования и управления ФГБОУ ВПО «Воронежский государственный университет инженерных технологий», г.Воронеж.
Кондрашова Е.В., д.т.н., профессор кафедры технического сервиса и технологии машиностроения ФГБОУ ВПО «Воронежский государственный аграрный университет имени императора Петра I», г.Воронеж.
Библиографическая ссылка
Бурмистров В.А. КОРРЕКТИРОВАНИЕ РЕЖИМОВ ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ ГРУЗОВЫХ АВТОМОБИЛЕЙ // Современные проблемы науки и образования. – 2014. – № 1. ;URL: https://science-education.ru/ru/article/view?id=11228 (дата обращения: 19.04.2024).