Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы

Фарахов М.И., Разинов А.И., Казанцев С.А., Величко М.Ю., Кузнецов В.А., Фарахов М.М., Бурмистров Д.А.

Получено сопряженное решение для газового турбулентного потока и жидкой ламинарной волновой пленки при восходящем прямотоке в плоском наклонном канале. Использована модель представления волн как шероховатости. Проведены экспериментальные исследования и сопоставление с ними результатов расчетов.

Статья в формате PDF

214 KB

В [1] предложена модель взаимодействия газового потока с пленкой жидкости, движущейся в ламинарном волновом режиме в вертикальной трубе, основанная на представлении волн как шероховатости. Используем данную модель для описания восходящего прямотока в плоском наклонном канале. В этом случае задача усложняется, так как профили потока импульса и скорости газа становятся не симметричными относительно плоскости, расположенной посередине между верхней стенкой щели и пленкой жидкости, текущей по нижней стенке. Для модели гладкой пленки это обуславливается отличием граничных условий для скорости газа – на верхней стенке она равна нулю, а на границе с пленкой . Для модели шероховатой пленки добавляется отличие в коэффициентах трения. Уравнения движения для гладкой пленки при этом не изменяются.

Запишем уравнение движения для газовой фазы, используя в данном случае прямоугольную систему координат, совместив плоскость x-z с поверхностью пленки, а ось x направим противоположно ее восходящему движению:

,                                                    (1)

где  – элемент тензора вязких напряжений (поток проекции импульса на ось x, направленный вдоль оси y),  – плотность газа,  – проекция ускорения свободного падения на ось x, – градиент давления вдоль оси x.

Проинтегрируем уравнение (1) с условием  при . Здесь y – расстояние от границы пленки жидкости, h – высота щели, δ – толщина пленки, b – расстояние от плоскости, расположенной посередине между верхней стенкой щели и пленкой жидкости, до плоскости с максимальной скоростью газа, соответствующей нулевому значению потока импульса. Причем величина b может быть как положительной, так и отрицательной. Получим:

.                                        (2)

На границе газа с пленкой жидкости, то есть при , :

.                                             (3)

Решим уравнение (3) относительно градиента давления:

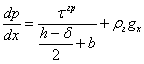.                                             (4)

Для нахождения потоков импульса на границе с пленкой  и на верхней стенке , а также величины b воспользуемся динамическими скоростями  и , а также их связью с коэффициентами трения Фаннинга  и :

,     (5)                   ,      (6)

,         (7)                   ,                       (8)

,              (9)                   ,                         (10)

,    (11)                 ,                     (12)

.                                 (13)

Для модели гладкой пленки

.                                                           (14)

Для модели шероховатой пленки

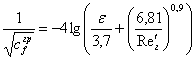,                                 (15)

Величину относительной шероховатости  запишем по аналогии с [1] в виде:

.                                                         (16)

В представленных уравнениях  – скорость газа на границе с пленкой жидкости,  – фиктивная скорость газа:

,                                                         (17)

где S – площадь поперечного сечения канала.

Коэффициент , характеризующий амплитуду волн, предлагается рассчитывать так же, как и в вертикальной трубе по уравнению [1]:

,                                       (18)

Градиент давления можно выразить не через , а через , проведя вывод уравнения, аналогичного (4)

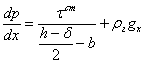.                                             (19)

Приравняв (4) и (19), а также выразив  и  с использованием динамических скоростей, можно получить явное выражение для величины b:

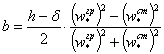.                                        (20)

Дополним полученную систему уравнениями движения пленки жидкости [1]:

скорость на границе пленки жидкости, взаимодействующей с газовым потоком:

;                                  (21)

средняя по сечению пленки скорость:

;             (22)

связь между толщиной пленки δ и линейной плотностью орошения :

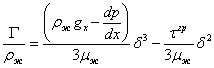.                            (23)

Таким образом, система уравнений становится замкнутой и позволяет найти , , , , , , , , , , , , , , b, решая численным методом систему 15 алгебраических уравнений (4)-(14), (17)-(20) для модели гладкой пленки или заменяя (14) на (15) – для шероховатой.

Для проверки адекватности предположенной модели была изготовлена экспериментальная установка с плоским каналом прямоугольного сечения высотой м, шириной м и длиной м, выполненным из стекла, позволяющая менять угол его наклона к горизонту , в которой измерялось потерянное давление  при восходящем прямотоке c помощью цифрового дифманометра. Схема установки приведена на рис. 1.

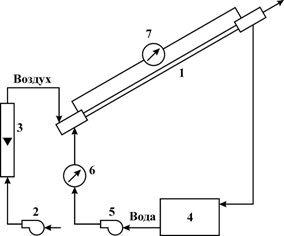
Рис. 1. Схема экспериментальной установки 1 – плоский канал; 2 – вентилятор; 3 – ротаметр; 4 – бак с водой; 5 – насос; 6 – расходомер; 7 – цифровой дифманометр.

Эксперименты проводились на системе воздух-вода при температуре 21°C. Вода для опытов была предварительно дистиллирована.

Расчетные значения потерянного давления определялись по формуле

                                                 (24)

Результаты некоторых расчетов приведены на рис. 2 и рис. 3

Рис. 2. Сопоставление экспериментальных и расчетных величин при кг/м×с; 

Рис. 3. Сопоставление экспериментальных и расчетных величин при кг/м×с; 

Анализ результатов расчетов показал, что для модели шероховатой пленки среднее расхождение с экспериментальными данными составляет 2,93%, а максимальное 12%, что не превышает погрешности эксперимента. Модель гладкой пленки дает систематическое занижение гидравлического сопротивления в среднем на 21,3%.

Таким образом, можно сделать вывод, что модель шероховатой пленки применима для описания волнового ламинарного её течения при восходящем прямотоке как в вертикальных трубах, так и в наклонной плоскости щели. Замкнутое сопряженное решение для потока турбулентного газа, взаимодействующего с ламинарной пленкой позволяет решать практические задачи сепарации аэрозолей, для расчета эффективности которых требуется знание динамической скорости.

СПИСОК ЛИТЕРАТУРЫ:

1.  Фарахов М.И., Разинов А.И., Казанцев С.А. Взаимодействие газового потока с пленкой жидкости при восходящем прямотоке в вертикальной трубе. // Современные проблемы науки и образования, №5, 2008. – С.77-81.

Библиографическая ссылка