Рассмотрим ламинарное стабилизированное стационарное течение жидкой пленки, взаимодействующей с газовым потоком. Поскольку толщина пленки δ, как правило, гораздо меньше радиуса кривизны канала, задачу можно рассматривать как плоскую с использованием прямоугольной системы координат.
Совместим поверхность, по которой движется пленка, с плоскостью z-x, а направление движения – с осью х. Запишем уравнения движения (1) и неразрывности (2) для рассмотренного случая:
![]() (1)
(1) ![]() (2)
(2)
где ![]() – элемент тензора вязких напряжений (поток проекции импульса на ось x, направленный вдоль оси y),
– элемент тензора вязких напряжений (поток проекции импульса на ось x, направленный вдоль оси y), ![]() – плотность жидкости,
– плотность жидкости, ![]() – проекция ускорения свободного падения на ось x,
– проекция ускорения свободного падения на ось x, ![]() – градиент давления вдоль оси x,
– градиент давления вдоль оси x, ![]() – проекция скорости жидкости на ось x.
– проекция скорости жидкости на ось x.
Интегрируя уравнение (1) с граничным условием ![]() при
при ![]() и полагая, что
и полагая, что ![]() , получим:
, получим:
![]() . (3)
. (3)
Для нахождения поля скорости в пленке подставим уравнение (3) в выражение для потока импульса за счет молекулярного механизма:
![]() , (4)
, (4)
и проинтегрируем с граничным условием прилипание на стенке ![]() . Получим:
. Получим:
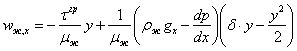 , (5)
, (5)
где ![]() – коэффициент молекулярной динамической вязкости.
– коэффициент молекулярной динамической вязкости.
Полагая ![]() , из уравнения (5) можно найти скорость на границе пленки, взаимодействующей с газовым потоком:
, из уравнения (5) можно найти скорость на границе пленки, взаимодействующей с газовым потоком:
![]() . (6)
. (6)
Определим среднюю по сечению пленки скорость жидкости с использованием (5) в виде:
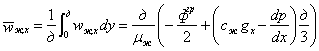 . (7)
. (7)
Это позволит связать толщину пленки и линейную плотность орошения ![]() следующим образом:
следующим образом:
![]() (8)
(8)![]()
Выражая среднюю скорость движения пленки из (8) и подставляя в (7), получим:
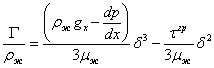 . (9)
. (9)
Уравнение (9) подробно анализировалось в работах [4, 5], где показана его работоспособность при восходящем прямотоке в вертикальных цилиндрических трубах. Однако необходимые значения касательного напряжения на границе газ-жидкость ![]() находились из экспериментальных данных по гидравлическому сопротивлению, как собственно, и
находились из экспериментальных данных по гидравлическому сопротивлению, как собственно, и ![]() . Таким образом, в полной мере теоретического решения для сопряженной задачи взаимодействия газового потока с жидкой пленкой получено не было.
. Таким образом, в полной мере теоретического решения для сопряженной задачи взаимодействия газового потока с жидкой пленкой получено не было.
Получим такое решение из уравнений движения (10) и неразрывности (11) для газовой фазы в вертикальной трубе. Для этого удобнее использовать цилиндрическую систему координат, совместив ось x с осью трубы и направив вниз:
![]() , (10)
, (10) ![]() . (11)
. (11)
Проинтегрировав уравнение движения с граничным условием ![]() , получим выражение для потока импульса:
, получим выражение для потока импульса:
![]() . (12)
. (12)
Поток импульса на границе раздела газ-жидкость ![]() найдем из (12) при условии
найдем из (12) при условии ![]() (R – внутренний радиус трубы):
(R – внутренний радиус трубы):
![]() . (13)
. (13)
Введем фиктивную скорость газа ![]() с использованием его объемного расхода
с использованием его объемного расхода ![]() :
:
![]() . (14)
. (14)
Радиус сечения, свободного для прохода газовой фазы, обозначим ![]() :
:
![]() . (15)
. (15)
Тогда истинную скорость газа относительно границы жидкой пленки и критерий Рейнольдса можно найти как
![]() , (16)
, (16) ![]() . (17)
. (17)
Использование новых штрихованных величин позволяет описать движение газового потока в трубе при наличии пленки жидкости соотношениями, полученными при ее отсутствии. Так градиент давления может быть выражен с помощью коэффициента гидравлического трения ![]() следующим образом:
следующим образом:
![]() . (18)
. (18)
Для замыкания системы уравнений (6), (7), (9), (13), (15), (16), (18), позволяющей найти ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() необходимо использовать выражение для
необходимо использовать выражение для ![]() . Если предположить, что поверхность пленки является гладкой, то для турбулентного режима движения газа, который реализуется при восходящем прямотоке, можно применить Формулу Блазиуса:
. Если предположить, что поверхность пленки является гладкой, то для турбулентного режима движения газа, который реализуется при восходящем прямотоке, можно применить Формулу Блазиуса:
![]() . (19)
. (19)
Тогда решая вышеуказанную систему алгебраических уравнений совместно с (17) и (19) можно найти как перечисленные величины, так и ![]() и
и ![]() .
.
Система этих девяти нелинейных уравнений решается численными методами. Подобная процедура была проделана в [3] для малых линейных плотностей орошения ![]() , при которых движение восходящей пленки можно считать безволновым. Расчетные толщины пленок воды при
, при которых движение восходящей пленки можно считать безволновым. Расчетные толщины пленок воды при ![]() кг/м×с и
кг/м×с и ![]() кг/м×с и фиктивных скоростях воздуха
кг/м×с и фиктивных скоростях воздуха ![]() м/с и
м/с и ![]() м/с достаточно хорошо совпали с экспериментальными данными [1] (относительная погрешность не превышала 7%). Однако увеличение плотности орошения менее чем в 2 раза, например, при
м/с достаточно хорошо совпали с экспериментальными данными [1] (относительная погрешность не превышала 7%). Однако увеличение плотности орошения менее чем в 2 раза, например, при ![]() кг/м×с, приводит к возрастанию относительной погрешности расчетов с использованием допущения гладкой пленки более 25% по сравнению с экспериментальными данными [5], авторы которых оценивают максимальную погрешность эксперимента 5%.
кг/м×с, приводит к возрастанию относительной погрешности расчетов с использованием допущения гладкой пленки более 25% по сравнению с экспериментальными данными [5], авторы которых оценивают максимальную погрешность эксперимента 5%.
Идея об аналогии при обтекании газовым потоком отдельных волн и бугорков в шероховатых трубах высказывалась П.Л. Капицей [2], однако и им до конца сопряженная задача взаимодействия газового потока с пленкой жидкости не была решена. Воспользуемся этой идеей для замыкания вышеприведенной системы уравнений, используя для этого известное выражение коэффициента гидравлического трения:
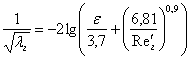 . (20)
. (20)
Величину относительной шероховатости ![]() запишем в виде:
запишем в виде:
![]() . (21)
. (21)
Единственный величиной, подлежащей определению, является коэффициент ![]() , характеризующий амплитуду волн. Решая обратную задачу, то есть, сопоставляя расчеты с использованием (20), (21) вместо (19) с экспериментальными данными по гидравлическому сопротивлению [5] было найдено соотношение:
, характеризующий амплитуду волн. Решая обратную задачу, то есть, сопоставляя расчеты с использованием (20), (21) вместо (19) с экспериментальными данными по гидравлическому сопротивлению [5] было найдено соотношение:
![]() , (22)
, (22)
где толщина пленки ![]() выражена в метрах.
выражена в метрах.
Результаты расчетов и сопоставление их с экспериментом [5] для системы вода-воздух, в вертикальной трубе ![]() м,
м, ![]() м (длина участка трубы, на котором измерялось гидравлическое сопротивление) приведены в таблице 1, где
м (длина участка трубы, на котором измерялось гидравлическое сопротивление) приведены в таблице 1, где ![]() – потерянное давление;
– потерянное давление; ![]() – средняя толщина пленки; верхние индексы: э – эксперимент, р – расчет, г – для гладкой пленки (19), ш–для шероховатой пленки (20), (21), (22). Расчетное потерянное давление определялось по уравнению:
– средняя толщина пленки; верхние индексы: э – эксперимент, р – расчет, г – для гладкой пленки (19), ш–для шероховатой пленки (20), (21), (22). Расчетное потерянное давление определялось по уравнению:
![]() . (23)
. (23)
Таблица 1. Сопоставление экспериментальных и расчетных величин при восходящем прямотоке в вертикальной трубе
| Г, кг/(м×с) | | | | | | | |
| 0,0185 | 20 30 40 | 0,95 1,65 2,55 | 0,98 1,72 2,65 | * 1,27 2,15 | 14,0 9,5 7,5 | 14,2 9,4 7,3 | * 12,0 8,5 |
| 0,0365 | 20 30 40 | 1,15 1,95 3,00 | 1,14 1,97 3,00 | ** 1,36 2,19 | 18,7 13 10 | 19,2 12,4 9,7 | ** 19,2 13,1 |
* – решение уравнения (9) относительно δ не имеет действительных положительных корней;
** – в результате решения средняя скорость жидкой пленки (7) направлена вниз, то есть осуществляется противоток.
Как видно из таблицы, максимальная погрешность расчетов с учетом шероховатости пленки не превышает 5%, то есть погрешности эксперимента. Расчеты же для гладкой пленки дают систематическое занижение потерянного давления и завышение толщины пленки приблизительно на 25%, а при скорости газа ![]() м/с либо не имеют решения, либо приводят к противотоку.
м/с либо не имеют решения, либо приводят к противотоку.
СПИСОК ЛИТЕРАТУРЫ:
1. Живайкин Л.Я. // Хим. маш. 1961. № 6. С. 25.
2. Капица П.Л. // ЖЭТФ. 1948. Т. 18. № 1. С. 19.
3. Разинов А.И. // Тепломассообменные процессы и аппараты химической технологии. Межвузовский тематический сборник научных трудов; КГТУ. Казань, 2002. С. 98.
4. Семенов П.А. // ЖТФ. 1944. Т14, № 7-8. С. 427.
5. Семенов П.А., Рейбах М.С., Горшков А.С. // Хим. пром. 1966. № 2. С. 213.
Библиографическая ссылка
Фарахов М.И., Разинов А.И., Казанцев С.А. ВЗАИМОДЕЙСТВИЕ ГАЗОВОГО ПОТОКА С ПЛЕНКОЙ ЖИДКОСТИ ПРИ ВОСХОДЯЩЕМ ПРЯМОТОКЕ В ВЕРТИКАЛЬНОЙ ТРУБЕ // Современные проблемы науки и образования. 2008. № 5. ;URL: https://science-education.ru/ru/article/view?id=1119 (дата обращения: 20.02.2026).



