Введение. Одними из тяжелых заболеваний, приводящих к инвалидности человека, являются врожденные и приобретенные аномалии развития опорно-двигательного аппарата, при лечении которых наибольшее распространение получил метод чрескостного остеосинтеза профессора Г.А. Илизарова.
Для регенерации костной ткани длинных конечностей названным методом первоначально использовался компрессионно-дистракционный аппарат с ручным приводом. Современные аппараты, реализующие данный метод, должны обеспечивать возможность амбулаторного лечения пациента и оптимальный цикл рабочих процессов, соответствующий естественным условиям регенерации костной ткани.
В ВлГУ разработан ортопедический аппарат автоматизированного остеосинтеза (далее - аппарат) с тремя независимыми прецизионными электромеханическими приводами (ЭМП) на базе шаговых микроэлектродвигателей (ШД) и планетарных роликовинтовых передач (ПРВП) в составе механической шарнирно-стержневой системы (ШСС) [1].
Аппарат (рис. 1), установленный на пациенте, с помощью ЭМП 1, 2 обеспечивает циклические продольные и угловые смещения неподвижного 5 и подвижного 6 колец, соединенных спицами 7, 8 с отломками костной ткани. С пульта управления микропроцессорной системы управления (МПСУ) задаются параметры движения отдельно для каждого ЭМП [7].

Рис. 1. Ортопедический аппарат автоматизированного остеосинтеза:
1, 2 – основной и дополнительные приводы; 3 – фиксатор углового положения основного привода; 4 – двухстепенной шарнир; 5, 6 – неподвижное и подвижное кольца; 7, 8 – спицы; 9 – отломки костной ткани
Постановка задачи исследования. Аппарат реализует широкий круг ортопедических задач. Вместе с тем результаты клинических испытаний потребовали, во-первых, решения ряда задач структурной модернизации функциональных частей аппарата – ШСС, ШД и МПСУ [3; 5-7], направленных на улучшение его главных показателей качества – массогабаритных, жесткостных и точностных.
Во-вторых, стало очевидным, что широкие возможности по выбору конструктивных параметров ПРВП делают актуальной задачу их оптимального сочетания, которое дает наилучшее проектное решение, соответствующее экстремальным значениям доминирующих критериев качества ШСС аппарата (минимальной массе и максимальной эквивалентной жесткости) при соблюдении необходимых требований по точности и плавности перемещения ПРВП – исполнительных механизмов ЭМП.
Динамическая модель мехатронной системы аппарата. Для постановки и решения математической задачи оптимального проектирования модернизированного аппарата, прежде всего, была построена динамическая модель мехатронной системы аппарата с целью ее всестороннего динамического анализа [4].
Предложенная модель включает в себя динамические модели всех функциональных частей аппарата.
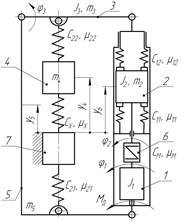
Рис. 2. Динамическая модель механической системы аппарата:
1 – ротор шагового двигателя; 2 – блок винта с роликами; 3 – подвижное кольцо; 4 – подвижный отломок кости; 5 – неподвижное кольцо с двумя электромеханическими приводами; 6 – сильфонная муфта; 7 – неподвижный отломок кости
Динамическая модель ШСС (рис. 2) представлена в виде пятимассовой системы с сосредоточенными параметрами, которая состоит из абсолютно твердых тел, соединенных между собой безынерционными упругодиссипативными элементами, подчинена стационарным, голономным связям и находится под действием потенциальных сил упругости и непотенциальных диссипативных сил.
Наиболее податливыми звеньями механической системы являются упругая муфта 6, хрящевая ткань, расположенная между подвижным 4 и неподвижным 7 отломками кости, а также связи между этими отломками и соответствующими кольцами. Кроме того, учтены диссипативные силы внутреннего трения в материале упругих звеньев, а также потери на трение в сопряжениях звеньев ПРВП.
За обобщенные координаты механической системы приняты: φ1 – угол поворота ротора ШД; φ2 – угол поворота блока винта с роликами; φ3 – угол поворота подвижного кольца; y4 – линейная координата подвижного отломка кости относительно неподвижного; y5 – линейная координата (деформационная) неподвижного кольца относительно неподвижного отломка кости; y6 – линейная координата (деформационная) блока винта с роликами относительно неподвижного отломка кости.
Дифференциальные уравнения движения механической системы аппарата в обобщенных координатах имеют вид [4]:
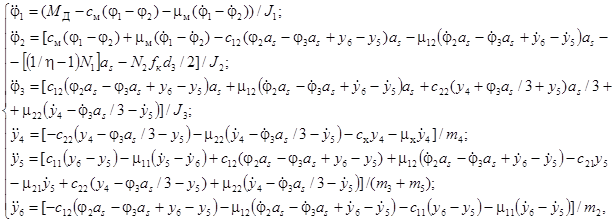 (1)
(1)
где МД – момент ШД; J1, J2, J3 – моменты инерции, соответственно, ротора ШД совместно с муфтой, блока винта с роликами и подвижного кольца, приведенные к оси винта; m2 – масса блока винта с роликами; m3 – масса подвижного кольца; m5 – суммарная масса неподвижного кольца и связанных с ним корпусных деталей ЭМП; см – крутильная жесткость сильфонной муфты; с11, с12 – линейные жесткости в сопряжениях роликов ПРВП с опорной и ходовой гайками, соответственно; с21, с22 – линейные жесткости связи колец, соответственно, с неподвижным и подвижным отломками кости; сх – линейная жесткость хрящевой ткани; μм – коэффициент демпфирования в сильфонной муфте; μ11, μ12 – коэффициенты демпфирования в сопряжениях роликов ПРВП с опорной и ходовой гайками, соответственно; μ21, μ22 – коэффициенты демпфирования связи колец, соответственно, с неподвижным и подвижным отломками кости; μx – коэффициент демпфирования хрящевой ткани; as=S/2π; S – перемещение ходовой гайки за оборот винта; η – КПД прямого хода ПРВП; N1=с12(φ2as–φ3as+y4–y5) – осевая сила в резьбовом сопряжении роликов с ходовой гайкой; N2=с11(y6–y5) – осевая сила в резьбовом сопряжении роликов с опорной гайкой; fk – приведенный коэффициент трения качения; d3 – средний диаметр резьбы опорной гайки.
Характер взаимодействия механической части аппарата с МПСУ определяется зависимостью МД от параметров движения, заданной динамической характеристикой ШД [8]
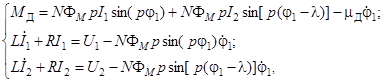 (2)
(2)
где μД – коэффициент вязкого трения ШД; N – число витков в обмотке статора; S – площадь поперечного сечения постоянного магнита; р – число пар магнитных полюсов ротора двигателя; λ – угол между обмотками ШД; I1, I2 – токи, поступающие на обмотки статора ШД с МПСУ; U1, U2 – напряжения на обмотках статора ШД; L – собственная индуктивность каждой фазы; R – сопротивление цепи обмотки статора.
Полагая МПСУ дифференцирующим звеном с замедлением с постоянной времени Тэл и коэффициентом усиления сигнала Ку, дифференциальные уравнения изменения напряжений на обмотках статора ШД представлены в виде:
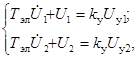 (3)
(3)
где Uу1, Uу2 – импульсы напряжения, формируемые МПСУ.
Динамический анализ. Динамический анализ мехатронной системы аппарата заключался в нахождении решений системы дифференциальных уравнений математической модели, соответствующих различным значениям параметров, для оценки влияния последних на качественные характеристики аппарата.
В связи с нелинейностью и высоким порядком системы дифференциальных уравнений решение получено на ЭВМ с использованием разработанного программного обеспечения на языке программирования Fortran методом Рунге-Кутты четвертого порядка.
Исследования проводились для режима, соответствующего одному циклу работы ЭМП при дистракции костной ткани, с поворотом ротора ШД на два угловых шага при шаговой частоте вращения 120 шаг/мин и расчетном перемещении подвижного отломка кости на 0,0070…0,0083 мм.
На рис. 3 представлены графики зависимостей изменения угла поворота ротора ШД, момента ШД и перемещения подвижного отломка кости от времени.
а)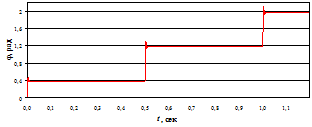 б)
б)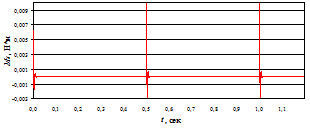
в)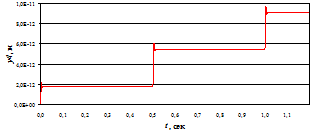
Рис. 3. Графики зависимостей угла поворота ротора шагового двигателя (а), момента шагового двигателя (б) и перемещения подвижного отломка кости (в) от времени
Из графика на рис. 3а видно, что угол поворота ротора за один угловой шаг составляет 0,785 рад. При этом за 8 угловых шагов ротор ШД поворачивается на 1 полный оборот, что соответствует паспортным характеристикам используемого ШД ДШ-25-0.001-45УХЛ4.
Полученный при моделировании максимальный вращающий момент (рис. 3б) при напряжении питания U=12 В составил 0,01 Н∙м, что в 10 раз превышает номинальный развиваемый момент ШД и соответствует экспериментально полученным значениям при шаговой частоте вращения 120 шаг/мин [3]. При кратковременных режимах работы в составе ЭМП такая перегрузка ШД вполне допустима и не приводит к его перегреву
Расчетное перемещение подвижного отломка кости за 2 полных шага ШД составило 0,0073 мм (рис. 3в), что лежит в пределах проектного диапазона перемещений.
В результате динамического анализа аппарата установлено, что определяющее влияние на его жесткость, массу и точность перемещения подвижного отломка кости оказывают жесткости связи отломков кости с кольцами (с21, с22), жесткости сопряжений роликов с опорной и ходовой гайками (с11, с12) в ПРВП, ее коэффициент полезного действия (η), средний диаметр резьбы опорной гайки (d3) и масса блока винта с роликами (m2).
С повышением жесткостей фиксации отломков кости с кольцами (с21, с22) повышается точность перемещения подвижного отломка кости, при этом их относительное влияние на эту точность существенно больше влияния жесткостей сопряжений роликов с гайками (с11, с12). Это дает возможность снизить почти на порядок жесткости с11 и с12 до значений, при которых их влияние на перемещения подвижного отломка кости будет сопоставимо с влиянием жесткостей с21 и с22. Воздействие жесткостей с11 и с12 на перемещение подвижного отломка кости соизмеримо, при этом снижение требований к этим жесткостям позволяет использовать в ЭМП исполнительные механизмы с меньшими размерами и массой.
Графики зависимости абсолютного перемещения подвижного отломка кости от времени при различных значениях жесткостей фиксации костных отломков с кольцами с21, с22 и жесткости хрящевой ткани сх представлены на рис. 4. Для большей информативности, приведенные графики даны для одного шага ШД в интервале времени от 0.498 до 0,518 с.
а)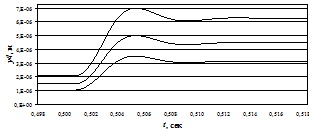 б)
б)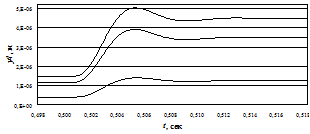
Рис. 4. Графики зависимости перемещения подвижного отломка кости от времени при различных значениях жесткостей: а) при сх=0.4 Н/мкм и с21=с22=0.1 Н/мкм – нижняя кривая, с21=с22=0.5 Н/мкм – средняя кривая, с21=с22=1 Н/мкм – верхняя кривая; б) при с21=с22=0.4 Н/мкм и сх=0 – верхняя кривая, сх=0.2 Н/мкм – средняя кривая, сх=0.4 Н/мкм – нижняя кривая
Из рис. 4а видно, что снижение жесткостей с21 и с22 ведет к уменьшению величины перемещения подвижного отломка кости за один шаг по нелинейному закону.
На рис. 4б показано, как при с21=с22=0,1 Н/мкм с увеличением жесткости сх снижается величина абсолютного перемещения подвижного отломка кости. По мере увеличения жесткостей с21 и с22 нижняя и средняя кривые сближаются с верхней.
При этом надо иметь в виду, что изменения жесткостей сопряжений звеньев аппарата, как правило, достигаются соответствующим изменением их массогабаритных параметров.
Полученные результаты влияния жесткостей показали, что изменение жесткостей некоторых звеньев аппарата практически не сказывается на перемещении подвижного отломка кости, и с целью снижения массы аппарата эти жесткости можно уменьшить. Кроме того, величины жесткостей звеньев зависят от жесткости хрящевой ткани сх, которая и будет определять их конечное значение, при условии перемещения подвижного отломка кости в пределах расчетного диапазона значений за цикл дистракции.
Повышение КПД η ПРВП позволяет использовать в ЭМП ШД с меньшим крутящим моментом, при сохранении требуемого развиваемого усилия на штоке. Уменьшение крутящего момента ШД пропорционально сказывается на его массе и габаритных размерах, а также ЭМП в целом. Но увеличение КПД ПРВП может привести к потере механизма самоторможения, а учитывая особенности работы ЭМП в аппарате [1], с целью экономии электроэнергии питающего аккумулятора не рекомендуется использовать исполнительные механизмы без самоторможения.
Постановка задачи оптимизации. Очевидно, что уменьшение массы аппарата приведет к уменьшению его эквивалентной жесткости. В связи с явной противоречивостью указанных критериев качества целесообразно ввести один обобщенный критерий – массу аппарата, отнесенную к его эквивалентной жесткости. Это достаточно простой и эффективный критерий для несущей механической ШСС аппарата, который необходимо минимизировать. Тогда целевую функцию можно представить в виде
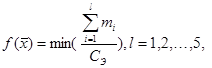 (4)
(4)
где ![]() – вектор варьируемых параметров;
– вектор варьируемых параметров; ![]() – суммарная масса звеньев механической системы аппарата;
– суммарная масса звеньев механической системы аппарата; ![]() – приведенная эквивалентная жесткость механической системы аппарата; k1, k1, k1 – коэффициенты, зависящие от взаимного расположения ЭМП на кольцах аппарата.
– приведенная эквивалентная жесткость механической системы аппарата; k1, k1, k1 – коэффициенты, зависящие от взаимного расположения ЭМП на кольцах аппарата.
По результатам проведенного динамического анализа, в качестве варьируемых выбраны следующие параметры: x1=c11=c12, x2=c21=c22, x3=η, x4=m2, x5=d3. Диапазон изменения каждого из них назначается исходя из конструктивных соображений
xjmin ≤ x j≤ xjmin, j=1,2…,5. (5)
Кроме того, необходимо учесть следующие функциональные ограничения. Во-первых, перемещение подвижного отломка кости за цикл работы не должно быть меньше минимального расчетного значения для этого перемещения y4 ≥ y4min.
Во-вторых, задача минимизации целевой функция должна решаться с учетом того, что усилия, возникающие в сопряжениях звеньев ПРВП аппарата во время его работы, не должны превышать максимальных проектных значений (N1, N2) ≤ Nmax. Причем оптимальное значение целевой функции должно обеспечиваться во всем диапазоне усилий.
Запишем эти ограничения в общем виде
![]() . (6)
. (6)
Тогда задачу оптимизации можно сформулировать следующим образом: выбрать такой вектор ![]() варьируемых параметров из допустимой области
варьируемых параметров из допустимой области
![]() , (7)
, (7)
при котором значение целевой функции будет наименьшим.
В связи с нелинейностью системы уравнений математической модели (1, 2, 3) поставленная задача оптимизации относится к классу задач нелинейного программирования при наличии параметрических (5) и функциональных (6) ограничений [2]. Проведенный анализ поведения целевой функции указывает на ее непрерывность в исследуемой области D (7), что позволяет воспользоваться для решения задачи оптимального проектирования одним из неградиентных методов, например одной из модификаций метода покоординатного спуска.
Выводы. Проведенные исследований динамической модели аппарата позволили обоснованно сформулировать целевую функцию и допустимую область изменения варьируемых параметров, назначить функциональные ограничения. В качестве итога сформулирована математическая задача оптимизации аппарата.
Рецензенты:
Кульчицкий А.Р., д.т.н., профессор, главный специалист ООО «Завод инновационных продуктов», г. Владимир.
Гоц А.Н., д.т.н., профессор кафедры «Тепловые двигатели и энергетические установки», ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир.
Библиографическая ссылка
Мамаев И.М. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ ОРТОПЕДИЧЕСКОГО АППАРАТА АВТОМАТИЗИРОВАННОГО ОСТЕОСИНТЕЗА. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11189 (дата обращения: 03.03.2026).



