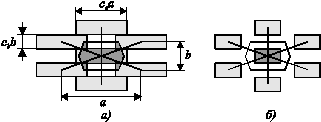Введение
Среди различных типов линзовых антенн известны антенны из неоднородного диэлектрика, обладающие замечательными свойствами. Одной из таких антенн является линза Микаэляна (ЛМ) [2]. Помимо применения в оптике [4], также возможно и применение данной линзы в СВЧ-диапазоне. Здесь такая линза может быть полезна, благодаря таким её особенностям, как плоская цилиндрическая форма, нулевое фокусное расстояние и возможность достичь малой толщины в широкой полосе частот [1].
Существует много методов реализации неоднородного диэлектрика, однако некоторые из них не позволяют реализовать единичное значение ε [5], более строгие методы зачастую сложны технологически и затратны [3]. В статье рассматривается метод, свободный от указанных недостатков.
Реализация неоднородной среды
Большинство методов реализации неоднородного диэлектрика основано на замене сплошной среды дискретной, например, с использованием перфорации или различных включений в однородную среду. Предлагаемый метод следует этому же принципу, но с определёнными отличиями.
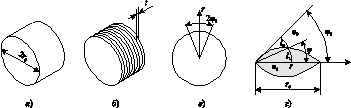
На рис. 1 проиллюстрировано изготовление цилиндрической неоднородной линзы из однородного листового диэлектрика. Вначале цилиндр разбивается в продольном направлении на тонкие слои, затем каждый слой разбивается на несколько секторов, и в каждом из секторов вдоль радиуса меняется коэффициент заполнения сектора материалом. Таким образом, слой приобретает форму N-лепесткового цветка, а задача расчёта сводится к определению формы лепестков как зависимости φ(r). Сами слои далее скрепляются вместе так, чтобы напротив промежутка в одном слое находился лепесток другого слоя (см. рис. 2)
|
|
|
|
Рис. 1 — Способ дискретизации непрерывной неоднородной среды: а) —исходная цилиндрическая линза, б) — разбиение цилиндра на элементарные слои, в) — разбиение слоя на секторы г) — частичное заполнение сектора диэлектриком |
Рис. 2 — пятилучевая ЛМ |
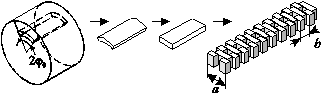
Описанная выше среда является периодической по двум цилиндрическим координатам: высоте z и углу φ, причём период равен d and 2π/N соответственно. Для расчёта периодических сред удобно использовать метод разложения по плоским волнам (PEM) [6], однако данный метод применяется только для решёток Браве, периодичных по декартовым координатам. Перейти от периодичности по цилиндрическим координатам к приодичности по декартовым координатам можно, осуществив своего рода предельный переход, как показано на рис. 3, если рассматривать достаточно малый сегмент цилиндра как параллелепипед. В таком случае мы перейдём к рассмотрению среды, фрагмент которой изображён на рис. 3 справа. Такая среда представляет собой двумерный фотонный кристалл (ФК), элементарная ячейка которого показана на рис. 4. Среда имеет продольный период b, равный удвоенной толщине слоя 2d и поперечный период а, равный 2πr/N. Величины ca и cb представляют собой коэффициенты заполнения, введённые для каждой из двух координат по отдельности. Изменение ε осуществляется изменением ca (рис. 4, а), а cb в данной задаче равен 1. Важно отметить, что a зависит от r, следовательно, расчёт ФК проводится для некоторого набора значений r от 0 до r0.
|
|
|
|
Рис. 3 — Переход к периодичности по декартовым координатам |
Рис. 4 — Элементарная ячейка ФК. Слева — 0,5 < ca < 1, справа — ca < 0,5 |
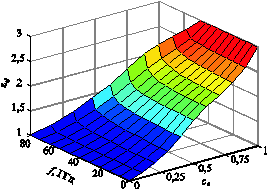
Для фотонных кристаллов характерно наличие запрещённых зон. Очевидно, что рабочий диапазон частот линзы Микаэляна будет ограничен сверху порогом первой запрещённой зоны fz1. Из графиков зонной структуры ФК, рассчитанных для различных ca и а, можно рассчитать зависимости ![]() . На рис. 5 и 6 показаны зависимости
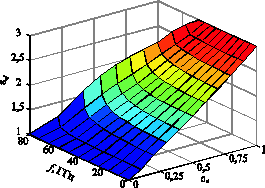
. На рис. 5 и 6 показаны зависимости ![]() для фиксированного значения а = 7 мм для двух поляризаций падающей волны. Из графиков можно видеть, что в достаточно широком диапазоне частот εef слабо зависит от частоты, зависимость начинает проявляться при приближении к запрещённой зоне. Различия рис. 5 и 6 показывают также, что среда обладает анизотропией, проявляющейся уже на низких частотах. Алгоритм численного расчёта геометрии лепестка сводится к следующим шагам:
для фиксированного значения а = 7 мм для двух поляризаций падающей волны. Из графиков можно видеть, что в достаточно широком диапазоне частот εef слабо зависит от частоты, зависимость начинает проявляться при приближении к запрещённой зоне. Различия рис. 5 и 6 показывают также, что среда обладает анизотропией, проявляющейся уже на низких частотах. Алгоритм численного расчёта геометрии лепестка сводится к следующим шагам:
- задать константы: ε1, r0, N, b, cb;
- задать набор значений r и, соответственно, а, набор значений ca;
- вычислить зависимости
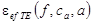 и
и 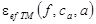 по методу PEM;
по методу PEM; - выбрать рабочий диапазон частот, на котором
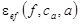 меняется слабо, и задать единственную усреднённую частоту f0;
меняется слабо, и задать единственную усреднённую частоту f0; - по полученным данным при помощи интерполяции найти зависимость
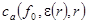 , где
, где 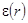 определяется по известному выражению для ЛМ [2].
определяется по известному выражению для ЛМ [2]. - по данным предыдущих расчётов вывести зависимость
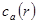 , которую и необходимо знать для вычисления профиля лепестка
, которую и необходимо знать для вычисления профиля лепестка 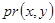 .
.
Алгоритм выполняется дважды для двух поляризаций падающей волны. Итоговая геометрия i-го лепестка ![]() определяется как
определяется как
![]() , (1)
, (1)
где yi — угол между плоскостью поляризации и осью ориентации лепестка.
|
|
|
|
Рис. 5 — Зависимость эффективной диэлектрической проницаемости ФК от частоты и коэффициента заполнения для а = 7 мм (ТМ-поляризация) |
Рис. 6 — Зависимость эффективной диэлектрической проницаемости ФК от частоты и коэффициента заполнения для а = 7 мм (ТЕ-поляризация) |
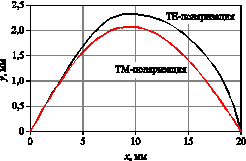
На рис. 7 показана геометрия лепестка, рассчитанного для двух поляризаций падающей волны, на рис. 8 показан вид всей линзы спереди.
Численное моделирование
Для подтверждения расчётов было проведено численное моделирование ЛМ в CST MWS. Линза имела радиус r0 = 20 мм, составлена из 1-мм слоёв диэлектрика с ε = 3, в качестве облучателя задан открытый конец волновода. Диапазон частот расчёта 20–40 ГГц.
|
|
|
|
|
Рис. 7 — Профили единичного лепестка, рассчитанные для r0 = 20 мм, N = 9 and f = 0 |
Рис. 8 — Фронтальный вид линзы |
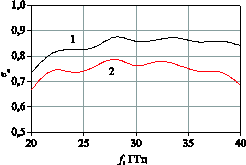
Рис. 9 — КИП для различных линз. 1 — рассчитанной с учётом анизотропии; 2 — рассчитанной без учёта анизотропии |
На рис. 9 приведено сравнение зависимостей апертурного КИП от частоты, рассчитанных для линзы, в которой учтена анизотропия (т.е. с лепестками, форма которых зависит от их ориентации относительно плоскости поляризации) и линзы без учёта анизотропии (лепестки одинаковой формы). Как можно видеть, учёт анизотропии приводит к выигрышу по КИП, кроме того, можно видеть, что КИП сохраняет высокий уровень в октавной полосе частот.
Заключение
Предложенный метод расчёта и реализации радиально-неоднородного диэлектрика позволяет создавать апертурные антенны, обладающие такими достоинствами, как широкая полоса рабочих частот, компактные размеры и простота изготовления. Линзы, изготовленные по предложенному методу, могут быть использованы в пассивных антенных решётках для расширения их частотного диапазона и упрощения диаграммообразующей схемы, а также в качестве самостоятельных апертурных антенн там, где важны малые продольные размеры структуры и отсутствие выдающихся частей, например, на борту транспортных средств. Результаты расчётов были подтверждены численным моделированием.
Работа выполнена во ФГАОУ ВПО «Сибирский федеральный университет» при поддержке Министерства образования и науки Российской федерации, договор № 02.G25.31.0041, соглашение № 14.A18.21.1287
Рецензенты:Слабко В.В., д.ф.-м.н., профессор, зав. кафедрой «Фотоника и лазерные технологии», федеральное государственное автономное образовательное учреждение высшего профессионального образования «Сибирский федеральный университет», г. Красноярск.
Беляев Б.А., д.т.н., профессор, зав. лабораторией электродинамики и СВЧ электроники, федеральное государственное бюджетное учреждение науки Институт физики им. Л.В. Киренского Сибирского отделения Российской академии наук, г. Красноярск.
Библиографическая ссылка
Александрин А.М., Гафаров Е.Р., Лемберг К.В., Лемберг К.В., Панько В.С., Поленга С.В., Рязанцев Р.О., Саломатов Ю.П. РЕАЛИЗАЦИЯ РАДИАЛЬНО-НЕОДНОРОДНОГО ДИЭЛЕКТРИКА И СОЗДАНИЕ АПЕРТУРНЫХ АНТЕНН НА ЕГО ОСНОВЕ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=10789 (дата обращения: 13.02.2026).