Одной из главных проблем современного инженерного образования в условиях модернизации высшей школы является проблема повышения качества образования и оценивания качества обучения в вузах [6, 8] и, в частности, анализ результатов входного тестирования в вузе [5, 7, 10]. В работах [1–3] проведен компьютерный статистический сравнительный анализ результатов входного контроля математических знаний школьной программы на основе аудиторной контрольной работы с проверкой ее преподавателями. Задание входного контроля в Томском политехническом университете (ТПУ) до 2011г. содержало 6 задач средней сложности (типа группы «В» в билетах ЕГЭ). В ТПУ, начиная с 2011г., наряду с вступительными испытаниями на основе результатов ЕГЭ по математике проводится входное тестирование (ВТ) математических знаний школьной программы на основе аудиторной контрольной работы в начале первого семестра. Задание ВТ для студентов-очников содержит 20 задач средней сложности (типа группы «В» в билетах ЕГЭ). В связи с этим представляет интерес статистический анализ результатов ВТ.
Все числовые результаты ВТ приведены к единой 5-балльной шкале (делением результата на соответствующий максимальный результат и умножением на пять). Созданная таким образом в MS Excel база данных использовалась далее в пакете Statistica [4] для статистического анализа данных.
Во ВТ набора 2011-2013 гг. участвовали студенты-очники первого курса ТПУ семи институтов [9]: кибернетики (ИК), природных ресурсов (ИПР), энергетического (ЭНИН), физики высоких технологий (ИФВТ), физико-технического (ФТИ), неразрушающего контроля (ИНК) и социально-гуманитарных технологий (ИСГТ).
Таким образом, в данной работе рассматривается 2-х факторная дисперсионная модель ВТ (3-х уровневый фактор «ГОД» и 7-и уровневый фактор «ИНСТИТУТ»).
Для оценки значимости отличия результатов ВТ математических знаний студентов ТПУ рассмотрим совместное распределение их выборок по годам 2011-2013 (рис. 1) по 5-ти балльной равномерной шкале. Согласно рис.1, очевидна положительная динамика результатов ВТ не только «абсолютная» (для 2012-2013 на фоне 2011 в интервале (3;5)), но и «качественная» (для 2013 на фоне 2012 в интервале (4;5)).
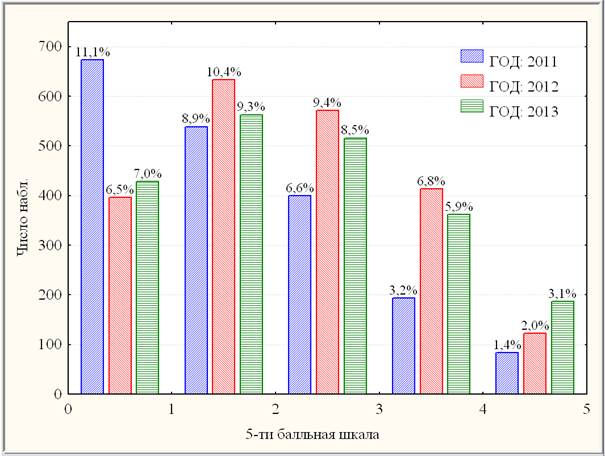
Рис.1. Составная гистограмма результатов ВТ ТПУ по годам 2011-2013
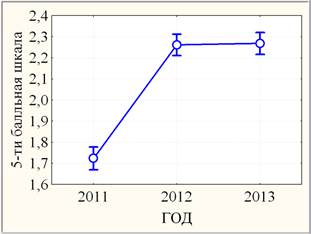
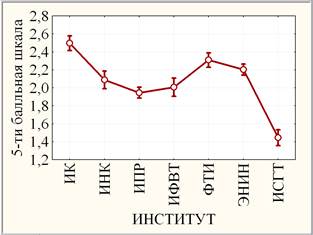
Значимость неоднородности результатов ВТ ТПУ по годам 2011-2013 (рис. 2, слева) оценивалась на основании однофакторного дисперсионного анализа фактора «ГОД», а по институтам - фактора «ИНСТИТУТ» (рис. 2, справа).
|
|
|
Рис. 2. Линейные графики средних ВТ ТПУ (круги) с ±95% доверительными интервалами (усы) по годам (слева:) и по институтам (справа)
Параметрический F-критерий оценивает различие результатов ВТ ТПУ по годам как высоко значимое (р < 0,0005) за счет высоко значимого отличия результатов ВТ ТПУ 2011г. (средний балл 1,724) от 2012-2013гг. при незначимом (р > 0,10) различии результатов ВТ ТПУ 2012г. (средний балл 2,261) и 2013г. (средний балл 2,268). Иными словами, влияние фактора «ГОД» на результаты ВТ ТПУ является высоко значимым. Аналогичная ситуация наблюдается с влиянием фактора «ИНСТИТУТ» на результаты ВТ ТПУ: результаты ВТ ТПУ являются высоко значимо неоднородными за счет, например, высоко значимого различия результатов ВТ институтов ИК (средний балл 2,496) и ИСГТ (средний балл 1,444).
Графики годовых средних баллов результатов ВТ по институтам с указанием 95 % доверительного интервала приведены на рис. 3.
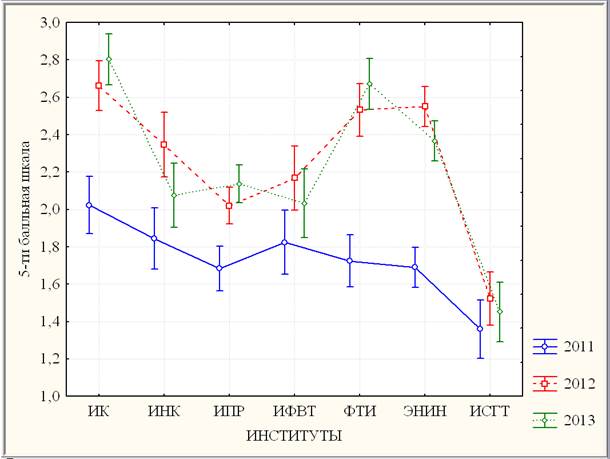
Рис. 3. Линейные графики годовых средних результатов ВТ по институтам
На основании однофакторного дисперсионного анализа оценена значимость неоднородности результатов ВТ для каждого года по совокупности институтов. Применение параметрического F-критерия дисперсионного анализа приводит к выводу о высоко значимой неоднородности результатов ВТ по совокупности институтов для любого года (и даже для наименее неоднородного 2011г.).
Параметрические (среднее, стандартная ошибка, ±95% границы доверительных интервалов, объем n) числовые характеристики выборок результатов ВТ студентов 7-и институтов ТПУ 2011-2013гг. приведены в табл. 1.
Таблица 1. Числовые характеристики выборок результатов ВТ по годам и институтам
|
Среднее |
Стд. ош. |
-95% |
+95% |
n |
||
|
2011 |
ИК |
2,023 |
0,079 |
1,869 |
2,178 |
217 |
|
2011 |
ИНК |
1,844 |
0,083 |
1,682 |
2,007 |
196 |
|
2011 |
ИПР |
1,684 |
0,061 |
1,565 |
1,803 |
364 |
|
2011 |
ИФВТ |
1,824 |
0,087 |
1,654 |
1,995 |
178 |
|
2011 |
ФТИ |
1,724 |
0,071 |
1,584 |
1,863 |
265 |
|
2011 |
ЭНИН |
1,690 |
0,054 |
1,584 |
1,796 |
461 |
|
2011 |
ИСГТ |
1,360 |
0,080 |
1,203 |
1,516 |
210 |
|
2012 |
ИК |
2,662 |
0,068 |
2,528 |
2,796 |
289 |
|
2012 |
ИНК |
2,346 |
0,089 |
2,173 |
2,520 |
171 |
|
2012 |
ИПР |
2,020 |
0,050 |
1,921 |
2,118 |
535 |
|
2012 |
ИФВТ |
2,168 |
0,087 |
1,996 |
2,339 |
176 |
|
2012 |
ФТИ |
2,533 |
0,072 |
2,392 |
2,674 |
260 |
|
2012 |
ЭНИН |
2,551 |
0,054 |
2,444 |
2,658 |
454 |
|
2012 |
ИСГТ |
1,523 |
0,073 |
1,380 |
1,666 |
253 |
|
2013 |
ИК |
2,803 |
0,070 |
2,667 |
2,939 |
278 |
|
2013 |
ИНК |
2,075 |
0,087 |
1,904 |
2,247 |
176 |
|
2013 |
ИПР |
2,136 |
0,052 |
2,035 |
2,237 |
507 |
|
2013 |
ИФВТ |
2,032 |
0,093 |
1,849 |
2,216 |
154 |
|
2013 |
ФТИ |
2,672 |
0,070 |
2,535 |
2,809 |
276 |
|
2013 |
ЭНИН |
2,366 |
0,054 |
2,260 |
2,472 |
460 |
|
2013 |
ИСГТ |
1,451 |
0,081 |
1,292 |
1,610 |
205 |
Согласно апостериорному критерию наименьшей значимой разности, эквивалентному t-критерию для числа независимых выборок больше двух, выделены для каждого года однородные (различающиеся незначимо, то есть на уровне значимости р > 0,10) группы институтов, расположенные в порядке убывания средних:
- 2011г.: {ИК, ИНК, ИФВТ}, {ИНК, ИФВТ, ФТИ, ЭНИН, ИПР}, {ИСГТ}. При этом ИК слабо значимо (0,05 < p=0,09 < 0,10) отличается от ИФВТ, но статистически значимо (0,005 < p=0,006 < 0,05) отличается от ФТИ, а ИНК незначимо (р = 0,12 > 0,10) отличается от ИПР, но высоко значимо (p < 0,0005) отличается от ИСГТ, который даже от ИПР отличается сильно значимо (0,0005 < p=0,001 < 0,005).
- 2012г.: {ИК, ЭНИН, ФТИ}, {ФТИ, ИНК}, {ИНК, ИФВТ}, {ИФВТ, ИПР}, {ИСГТ}. При этом ИК незначимо (р = 0,19 > 0,10) отличается от ФТИ, но статистически значимо (0,005 < p=0,006 < 0,05) отличается от ИНК. Аналогично ФТИ и ИФВТ, а также ИНК и ИПР, различаются сильно значимо (0,0005 < p=0,001 < 0,005). ИСГТ даже от ИПР отличается высоко значимо (p= < 0,0005).
- 2013г.: {ИК, ФТИ}, {ЭНИН}, {ИПР, ИНК, ИФВТ}, {ИСГТ}. При этом ФТИ незначимо (р = 0,18 > 0,10) отличается от ИК, но статистически значимо (0,005 < p=0,006 < 0,05) отличается от ЭНИН.
Графики средних баллов результатов ВТ по математике с указанием 95 % доверительного интервала для каждого института по годам, приведенные на рис. 4, дают представление о динамике качества приема на 1 курс.
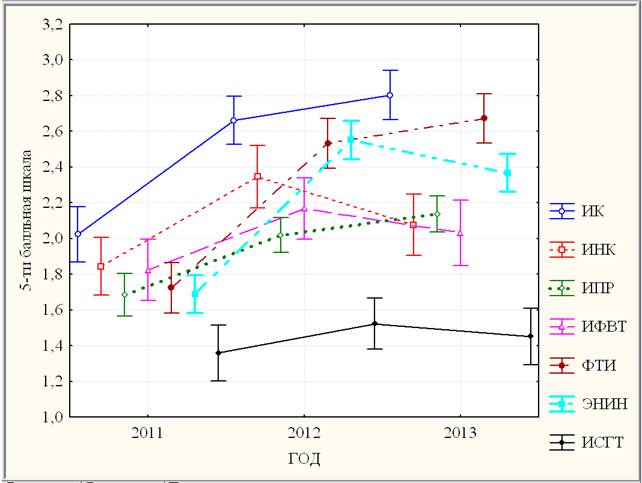
Рис. 4. Средние ВТ институтов по годам с ±95% доверительными интервалами
Заметим, что динамика качества приема ИСГТ является незначимой: даже результаты ВТ 2011г. (средний балл 1,36) и 2012г. (средний балл 1,52) различаются незначимо (р = 0,13 > 0,10).
Согласно рис.4, все остальные институты имеют значимую положительную динамику в период 2011-2012гг. Далее ИК, ФТИ и ИПР имеют положительную незначимую динамику в период 2012-2013гг.: даже в случае самой сильной положительной динамики в ИПР результаты ВТ 2012г. (средний балл 2,020) и 2012г. (средний балл 2,136) различаются незначимо (р = 0,105 > 0,10). Среди остальных институтов в период 2012-2013гг. ИФВТ имеет отрицательную незначимую динамику, а ИНК и ЭНИН – отрицательную статистически значимую (0,005 < p < 0,05) динамику.
Проведенный статистический анализ результатов входного тестирования по математике студентов-первокурсников позволяет преподавателю выяснить реальную подготовленность первокурсников к изучению курса высшей математики. Результаты тестирования использовались при формировании групп для дополнительных занятий по математике и для составления программы работы с этими группами, включавшей в себя, помимо текущей тематики, ряд разделов из элементарной математики.
Выводы
1. Результаты ВТ математических знаний студентов ТПУ имеют положительную динамику не только «абсолютную» (для 2012-2013 на фоне 2011 в интервале (3;5) 5-ти балльной шкалы), но и «качественную» (для 2013 на фоне 2012 в интервале (4;5)).
2. Различие результатов ВТ ТПУ по годам оценивается как высоко значимое (р < 0,0005) за счет высоко значимого отличия результатов ВТ ТПУ 2011г. (средний балл 1,724) от 2012-2013гг. при незначимом (р > 0,10) различии результатов ВТ ТПУ 2012г. (средний балл 2,261) и 2013г. (средний балл 2,268).
3. Результаты ВТ ТПУ являются высоко значимо неоднородными по институтам за счет, например, высоко значимого различия результатов ВТ институтов ИК (средний балл 2,496) и ИСГТ (средний балл 1,444). Для каждого года выделены однородные (различающиеся незначимо) группы институтов.
4. Оценена динамика качества приема на 1 курс по институтам: незначимая по ИСГТ, для остальных институтов в период 2011-2012гг. значимая положительная, но в период 2012-2013гг. ИК, ФТИ и ИПР имеют положительную незначимую динамику, ИФВТ имеет отрицательную незначимую динамику, а ИНК и ЭНИН – отрицательную статистически значимую динамику.
Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Михальчук А.А., Арефьев В.П., Филипенко Н.М. ДИСПЕРСИОННЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ ВХОДНОГО ТЕСТИРОВАНИЯ МАТЕМАТИЧЕСКИХ ЗНАНИЙ В ТЕХНИЧЕСКОМ ВУЗЕ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10691 (дата обращения: 22.02.2026).