Введение
Конвейеры различной длины с цепным тяговым органом нашли широкое применение в различных отраслях промышленности благодаря конструкторской и научно-исследовательской работе, проведенной советскими учеными. В 30-х годах XX века Г. Ганфштенгелем были получены аналитические зависимости по определению динамических сил, величина которых оказывается прямо пропорциональной квадрату скорости движения конвейера [4]. Как оказалось, эта теория верна только для тихоходных конвейеров. В 40-х годах Спиваковским А.О. и В.Д. Кружковым были исследованы динамические усилия в тяговом органе скребкового конвейера, и было доказано, что частота колебаний усилий в тяговой цепи пропорциональна повороту звездочки на один зуб [9]. А.А. Долголенко предложил рассматривать тяговую цепь конвейера как систему с распределенными параметрами. Было доказано существенное влияние динамических характеристик на колебательные процессы [5]. Динамика пластинчатых, скребковых конвейеров была исследована в работах к.т.н. В.К. Смирнова, к.т.н. В.П. Крота [8], Д.М. Беленького [1; 2] и проф. В.Н. Маценко [6]. В результате большой научной работы была создана теория движения тяговых цепей [7].
В современном производстве широкое применение получили поточные автоматические линии на базе цепных конвейеров. Самым сложным с точки зрения нагрузок является использование пластинчатых конвейеров в горнодобывающей промышленности [10]. Сложные условия эксплуатации и специфика работы обусловливают низкий ресурс, что приводит к значительным простоям оборудования, так, 50% простоев происходит из-за его отказов, а ремонтные работы одни из самых трудоемких.
При интенсификации производства улучшение эксплуатационных характеристик тяговой цепи, безусловно, скажется на бесперебойной работе всего механизированного комплекса [12].
Определение амплитуды динамических смещений
Причины выхода из строя конвейера могут быть различны, но одна из основных - динамические нагрузки, на возникновение которых оказывают влияние колебательные процессы. Исследования колебательных процессов в тяговых органах различных цепных конвейеров показали, что в спектре колебаний обязательно присутствует частота собственных свободных колебаний тягового органа. Это можно объяснить возбуждением последних периодическими ударами ходовых роликов на стыках направляющих у пластинчатых конвейеров [13].
Удар элементов тягового органа о стык направляющих можно представить как мгновенное изменение скорости на величину
![]()
![]()
![]()
![]() , (1)
, (1)
где ![]() - несобственная функция Дирака;
- несобственная функция Дирака;
![]() - координаты местонахождения стыков направляющих;
- координаты местонахождения стыков направляющих;
![]() - полное смещение сечения тягового органа, включающее динамическое
- полное смещение сечения тягового органа, включающее динамическое ![]() , статическое
, статическое ![]() смещение и переносное движение
смещение и переносное движение ![]() ;
;
![]() - отдельные моменты времени, соответствующие шагу ходовых роликов
- отдельные моменты времени, соответствующие шагу ходовых роликов ![]() ;
;
![]() - равномерная (средняя) скорость движения тягового органа.
- равномерная (средняя) скорость движения тягового органа.
Уравнение относительно динамического смещения тягового органа, двигающего по гладким направляющим, для расчетной схемы, включающей одну концевую звездочку и тяговый орган в виде упруговязкого тела, может быть записано в виде [11]:
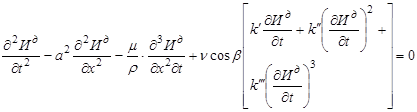 (2)
(2)
с граничными условиями
![]()
![]()
![]() =0 - натяжение сбегающей ветви ниже критического (3)
=0 - натяжение сбегающей ветви ниже критического (3)
![]()
![]()
![]() -
-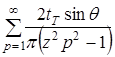 - смещение, задаваемое приводной звездочкой, (4)
- смещение, задаваемое приводной звездочкой, (4)
где ![]() - коэффициент диссипации энергии колебаний;
- коэффициент диссипации энергии колебаний;
![]() - приведенная плотность тягового органа;
- приведенная плотность тягового органа;
![]() - скорость распространения упругой волны;
- скорость распространения упругой волны;
![]() - коэффициенты разложения в ряд Тейлора приведенного коэффициента сопротивления движению;
- коэффициенты разложения в ряд Тейлора приведенного коэффициента сопротивления движению;
![]() - шаг цепи;
- шаг цепи;
![]() - число зубьев звездочки;
- число зубьев звездочки;
![]() ;
; ![]() ;
;
![]() - погонная нагрузка транспортируемого материала и тягового органа;
- погонная нагрузка транспортируемого материала и тягового органа;
![]() - частота возмущения приводной звездочки;
- частота возмущения приводной звездочки;
![]() - высшие гармоники.
- высшие гармоники.
С учетом малого параметра ![]() , применяя метод усреднения Н.Н. Боголюбова – Ю.А. Митропольского [3], уравнения (1)-(4) можно записать
, применяя метод усреднения Н.Н. Боголюбова – Ю.А. Митропольского [3], уравнения (1)-(4) можно записать
![]()
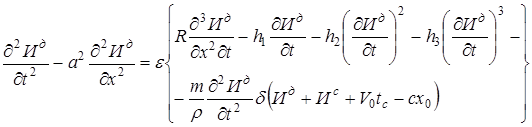 . (5)
. (5)
![]()
![]() =0. (6)
=0. (6)
![]()
![]()
![]() =
=![]() . (7)
. (7)
где ![]()
Решение ![]() ищем в виде суммы
ищем в виде суммы
![]() , (8)
, (8)
где ![]() - амплитуда колебаний;
- амплитуда колебаний;
![]()
![]() - фаза колебаний.
- фаза колебаний.
Функция ![]() выбирается так, чтобы она удовлетворяла граничным условиям (6)-(7) и уравнению (5)
выбирается так, чтобы она удовлетворяла граничным условиям (6)-(7) и уравнению (5)
![]() . (9)
. (9)
Тогда функция ![]() будет удовлетворять нулевым граничным условиям.
будет удовлетворять нулевым граничным условиям.
Для внерезонансных колебаний уравнение для амплитуды ![]() и фазы
и фазы ![]() записывается
записывается
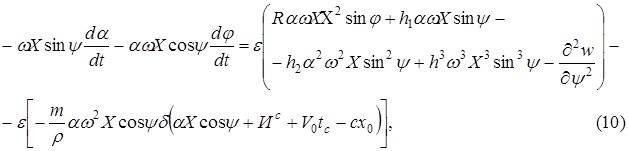
где ![]() - фундаментальная функция;
- фундаментальная функция;
![]() - собственное число.
- собственное число.
Учитывая периодичность ![]() и
и ![]() и используя свойства несобственной функции, получаем систему уравнений для определения амплитуды
и используя свойства несобственной функции, получаем систему уравнений для определения амплитуды ![]() и фазы
и фазы ![]() во внерезонансном режиме
во внерезонансном режиме
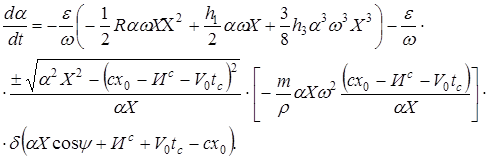
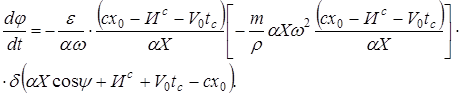 (12)
(12)
Интерес представляет лишь случай ![]() >
>![]() .
.
Пусть ![]() и
и ![]() корни уравнения
корни уравнения ![]() , принадлежащие отрезку
, принадлежащие отрезку 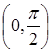 и
и 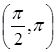 .
.
Тогда 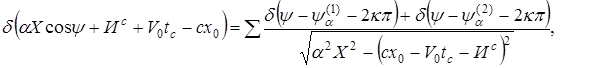 (13)
(13)
![]()
Система уравнений (11)-(12) может быть записана как
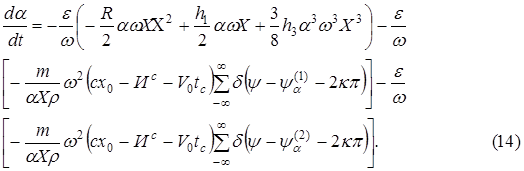
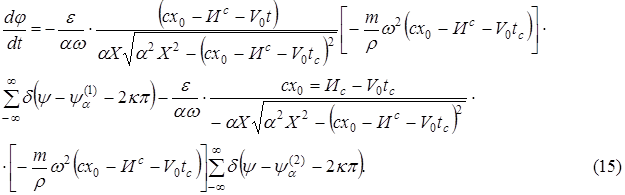
Но 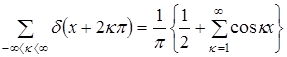 .
.
Тогда
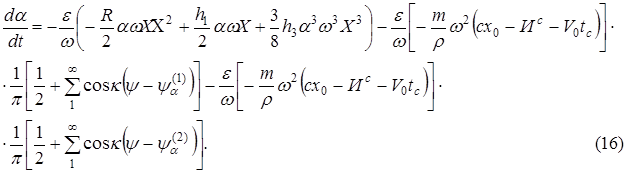
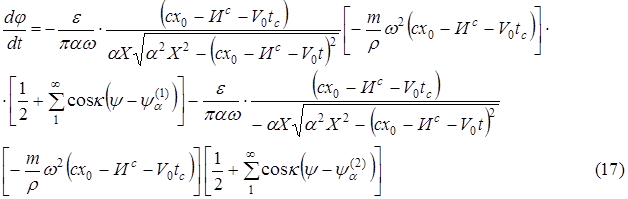
Учитывая ортогональность функции ![]() , получаем в качестве первого приближения
, получаем в качестве первого приближения
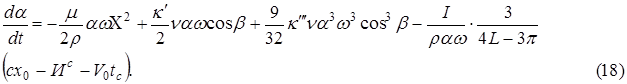
Рассматривая стационарный режим колебаний, имеем
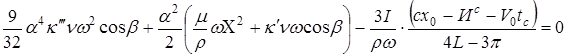 (19)
(19)
Амплитуда динамических смещений
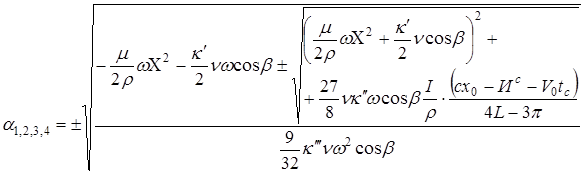 (20)
(20)
Анализ решения показывает, что при отсутствии ударов на стыках и выполнении условий:
![]() - т.е. коэффициент сопротивления движения тягового органа с увеличением скорости уменьшается;
- т.е. коэффициент сопротивления движения тягового органа с увеличением скорости уменьшается;
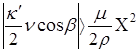 - т.е. возмущение преобладает над демпфированием; появляются автоколебания.
- т.е. возмущение преобладает над демпфированием; появляются автоколебания.
Поскольку ![]() , то последние возникают лишь в длинных конвейерах.
, то последние возникают лишь в длинных конвейерах.
Уравнение первого приближения при наличии ударов на стыках дает осредненную амплитуду колебаний, на величину которой влияют положительно: величина импульса; частота ударов; и отрицательно – длина конвейера.
Вывод
Таким образом, периодические удары на стыках увеличивают амплитуду низкочастотных собственных колебаний тягового органа конвейера.
Рецензенты:
Жизняков А.Л., д.т.н., профессор, зав. кафедрой систем автоматизированного проектирования, МИ (филиал) ВлГУ, г. Муром.
Андрианов Д.Е., д.т.н., профессор, зав. кафедрой информационных систем, МИ (филиал) ВлГУ, г. Владимир.
Библиографическая ссылка
Лазуткина Н.А. ИССЛЕДОВАНИЕ ПРОДОЛЬНОЙ ДИНАМИКИ ЦЕПНОГО КОНВЕЙЕРА // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10690 (дата обращения: 16.02.2026).



