Введение
В практических целях активные магнитные подшипники (АМП) нашли применение, в первую очередь, в качестве подшипников для подвеса роторов высокоскоростных электрических машин, работающих в условиях, не допускающих использование традиционных подшипников качения или скольжения [7]. Так, например, электрогазоперекачивающие агрегаты (ЭГПА) газотранспортной системы, оборудованные электромагнитным подвесом ротора, не нуждаются в ежедневном обслуживании, могут функционировать при экстремально низких температурах, а также в условиях повышенного радиоактивного фона. Второй по значению областью применения АМП являются испытательные стенды авиационных двигателей, так как скорости, которые должны развиваться стендом для проверки характеристик двигателей и проведения необходимых исследований, высоки, то применение традиционных подшипников является неэффективным.
Активный магнитный подшипник является сложным электротехническим устройством, состоящим из управляемых электромагнитов и системы автоматического управления токами (напряжениями) их обмоток. Для решения задач управления путем предварительного моделирования поведения системы в целом необходима математическая модель управляемого электромагнита, описывающая нелинейных характер генерируемых электромагнитных сил. Данные силы воздействуют на ротор электрической машины и обеспечивают тем самым бесконтактный электромагнитный подвес, что позволяет обеспечивать бесперебойную работу с высокой скоростью вращения (до 120000 об/мин) [2].
По расположению управляемых электромагнитов различают различные конфигурации АМП (рис. 1), а следовательно, и различные математические модели. Однако в современных промышленных электрических машинах наиболее часто используется АМП, имеющие схему расположения электромагнитов, представленную на рис. 1 г. Таким образом, рассматриваемая далее математическая модель описывает процесс формирования электромагнитных сил АМП, построенный по принципу полного магнитного подвеса с Х-образным расположением осей.
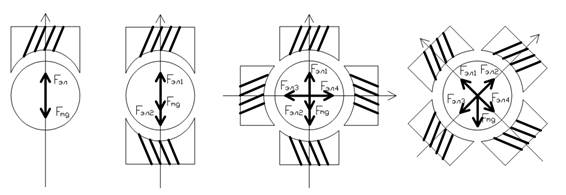
а. б. в. г.
Рис. 1 – Схемы расположения управляемых электромагнитов в АМП: а. – односторонний электромагнитный подвес, б. – двухсторонний электромагнитный подвес, в. – полный электромагнитный подвес, г. – полный электромагнитный подвес с Х-образным расположением осей
Рассматриваются две математические модели радиальных активных магнитных подшипников – полная и упрощенная. Полная математическая модель АМП предназначена для исследования нелинейных свойств электромагнита и учета влияния этих нелинейностей на динамику ротора. Упрощенная математическая модель АМП применима для целей моделирования в Matlab/Simulink.
1. Упрощенная математическая модель радиального активного магнитного подшипника
Для формирования математической модели электромагнитного подшипника для дальнейшего исследования в Matlab рассмотрим уравнение равновесия ротора в магнитном поле [1]:
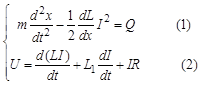
где Q – возмущающая сила, U – напряжение питания, приложенное к обмоткам электромагнита, L1 – индуктивность обмотки электромагнита, соответствующая потоку рассеяния, R – активное сопротивление обмотки электромагнита, ![]() – магнитная сила.
– магнитная сила.
Уравнение (1) описывает преобразование магнитной энергии опоры в кинетическую энергию ротора и является уравнением равновесия инерционной системы ротора. Уравнение (2) описывает процесс преобразования электрической энергии сети питания в магнитную энергию опоры и является уравнением электрического равновесия в цепи питания электромагнита.
Обычно насыщение в магнитной цепи электромагнита отсутствует, поэтому в первом приближении потокосцепление и ток электромагнита связаны линейной зависимостью [6]
![]()
Уравнение (3) является уравнением равновесия магнитной цепи опоры. С учетом (3) уравнения электромеханическое преобразование энергии можно представить в следующем виде, где ψ – потокосцепление обмотки электромагнита, соответствующее потоку в воздушном зазоре:
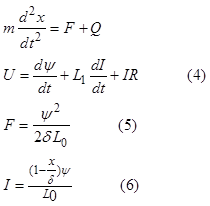
Уравнения (2), (3) и (4) образуют математическую модель магнитной опоры. Входными переменными этой модели являются напряжение питания обмотки U и положение ротора x. Положение ротора может изменяться в пределах зазора страховочного подшипника. Выходными переменными модели являются магнитная сила F и ток обмотки I. Диапазон изменения выходных переменных определяется максимальным тяговым усилием Fm.
Максимальное потокосцепление ψm связано с максимальным тяговым усилием соотношением: ![]()
Максимальный ток Im с максимальным потокосцеплением связан соотношением:
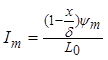 ,
,
которое при центральном положении ротора (x = 0) принимает вид: ![]() .
.
Максимально возможное значение возмущающей силы обозначим как Qm. Максимально возможное напряжение питания обозначим Um. Значение напряжения питания, при котором по обмотке протекает постоянный ток Im0 и электромагнит развивает максимальное усилие Fm,
![]()
Приняв перечисленные выше максимальные значения параметров модели за базовые, можно перейти к относительным переменным:
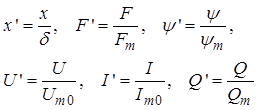
После ввода оператора дифференцирования s уравнения электромагнитного преобразования энергии в магнитной опоре принимают более простой вид:
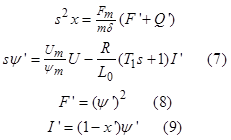
где ![]() – постоянная времени, соответствующая индуктивности рассеяния.
– постоянная времени, соответствующая индуктивности рассеяния.
Учёт насыщения железа в математической модели может быть осуществлён путём введения степенной функции потокосцепления в уравнение (9) в следующем виде:
![]()
где g и n – коэффициент насыщения и показатель степени, которые определяются по расчётным токовым характеристикам магнитной опоры.
Для реализации математической модели в соответствии с уравнениями (7) – (9) использован пакет программ математического моделирования Matlab/Simulink [3]. Результаты моделирования представлены на рисунке 2.
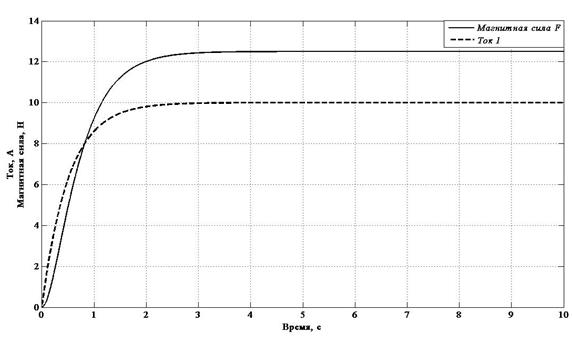
Рис. 2 – результаты расчета магнитных сил и тока по упрощенной модели АМП
2. Полная математическая модель радиального активного магнитного подшипника
Формируется полная модель для четырехканального АМП. Каждый канал состоит из четырех катушек, уложенных на четыре зубца. При этом в трех пазах находится проводники двух катушек канала, в двух пазах находятся проводники одной катушки канала и катушки смежного канала.
В отличие от упрощенной модели радиального АМП, полная модель является более точной и формирует табличную нелинейную зависимость магнитной силы от перемещения ротора и тока обмоток электромагнитов.
Построение модели ведется в цилиндрических координатах, где ориентация каналов принимается при отсчете угла от вертикальной оси снизу против часовой стрелки. Направление центральных осей каналов обозначено через β1 … β4 .
При построении модели используются следующие обозначения:
I – ток катушки канала;
dr – перемещение ротора от нейтрального положения в цилиндрической системе координат;
θ – направление перемещения;
Mr – полный вес ротора;
Jp – полярный момент инерции;
Jxy – поперечный момент инерции;
d – номинальный рабочий зазор;
dd - максимальное отклонение зазора от номинального значения;
R1 - радиус расточки статора подшипника;
l - активная длина подшипника;
lp - «база» подшипника;
ω - количество витков;
ωz - частота вращения ротора (рабочая);
Полная модель радиального АМП строится по алгоритму, представленному ниже.
1. Расчет изменения рабочего зазора при перемещении ротора
Изменение рабочего зазора – определение минимума функции от ξ:
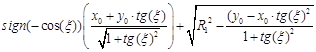 (10)
(10)
где ![]() ,
, ![]() .
.
2. Расчет собственной индуктивности канала в зависимости от смещения ротора определяется как:
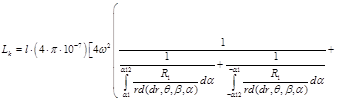
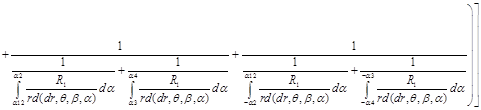 (11)
(11)
3. Расчет взаимная индуктивность со смежным каналом.
Аппроксимированное значение взаимной индуктивности со смежным каналом определяется согласно выражению:
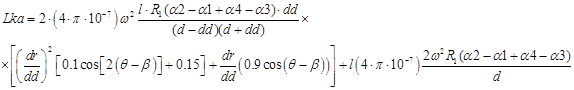 (12)
(12)
Табличная зависимость, рассчитанная согласно формулам (11-12), используется в обобщенной модели системы в виде численных значений компонента LookupTable при реализации модели АМП в Matlab/Simulink. Графическое представление зависимости (12) приведено на рисунке 3.
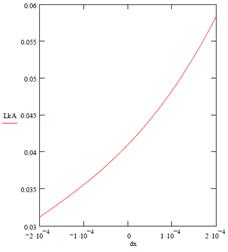
Рис. 3 – Зависимость индуктивности от перемещения
4. Выражение энергии в зазоре через индуктивность:
![]()
5. Зависимость магнитной силы от координаты:
![]()
6. Характеристики поля в зазоре ![]() ,
, ![]()
7. Расчет тягового усилия как интеграла от давления поля
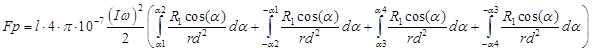 (13)
(13)
![]() (14)
(14)
8. Представление магнитной силы в виде полинома от перемещения при разложении в ряд Тейлора.
9. Энергия системы
Энергия системы при вращении ротора: ![]()
Энергия качания ротора: ![]() , где
, где ![]() – частота качания ротора вокруг центра масс.
– частота качания ротора вокруг центра масс.
10. Рассматривается уравнение состояния магнитомеханической двухмассовой системы с пятью степенями свободы. Сложное движение разделяется на поступательное (центр масс) и вращательное (относительно центра масс).
Построение функции Лагранжа:
Кинетическая энергия
Выражение для кинетической энергии поступательного движения имеет вид:
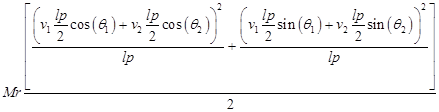 (15)
(15)
где с достаточной степенью точности: ![]() ,
, ![]()
Выражение для энергии колебательного движения имеет вид:
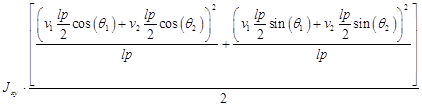 (16)
(16)
Энергия вращательного движения определяется согласно формуле:
![]() (17)
(17)
Прецессия ротора вычисляется как:
![]() (18)
(18)
Потенциальная энергия
Гравитационная энергия:
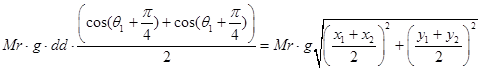 (19)
(19)
Энергия магнитного поля:
![]()
![]() (20)
(20)
Построим систему уравнений в координатах датчиков v,w для простоты и наглядности назовем координаты x и y. Обобщенные координаты: ![]()
![]()
Лагранжиан: ![]()
Согласно выражениям (15)-(17) кинетическая энергия магнитомеханической двухмассовой системы может быть представлена в виде [5] :
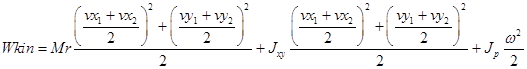 (21)
(21)
Потенциальная энергия системы при учете (20) и введения обобщенных координат:
![]()
![]()
![]() (22)
(22)
В результате решения функции Лагранжа строится система дифференциальных уравнений ![]() :
:
11. Уравнение проверки достаточности напряжения
![]() (23)
(23)
12. Значения тяговых усилий (магнитных сил) АМП
Точное значение силы тяжения одного магнита:
![]() (24)
(24)
Табличная зависимость магнитной силы, рассчитанная согласно формуле (24), используется в обобщенной моделе системы в виде численных значений компонента LookupTable при реализации модели в Matlab/Simulink [4]. Семейства кривых, построенные по данным расчетным значениям магнитных сил, приведены на рис. 4.
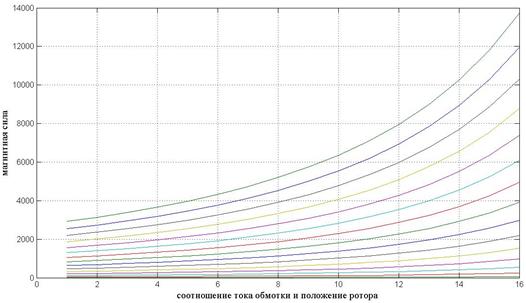
Рис. 4 – зависимость магнитной силы от тока в обмотке электромагнита и текущего положения ротора в воздушном зазоре
Существует также поперечная сила электромагнита при поперечном смещения ротора относительно оси магнита.
![]()
(25)
3. Разработка автономного программного приложения для расчета электромагнитных характеристик радиального АМП.
Для полной математической модели радиального АМП разработано автономное программное приложение, реализующее расчет и визуализацию основных электромагнитных характеристик АМП.
Алгоритм программы реализует автоматический расчет следующих характеристик радиального АМП: тяговое усилие, энергия поля, индуктивность канала, изменение рабочего зазора, сила тяжения одного магнита, поперечная электромагнитная сила.
Программа обладает пользовательским интерфейсом, основная экранная форма которого представлена на рис. 5.
Параметры для расчета (полный вес ротора, моменты инерции, номинальный рабочий зазор, радиус статора, активная длина подшипника и т.д.) вводятся в программу с помощью диалоговых полей. Рассчитанные значения отображаются в виде графиков и в табличном виде. Любой график или таблица может быть сохранена пользователем.
Рассчитанные значения индуктивности и силы тяжения (электромагнитные силы) заносятся пользователем в математическую модель АМП, сформированную в Matlab/Simulink.
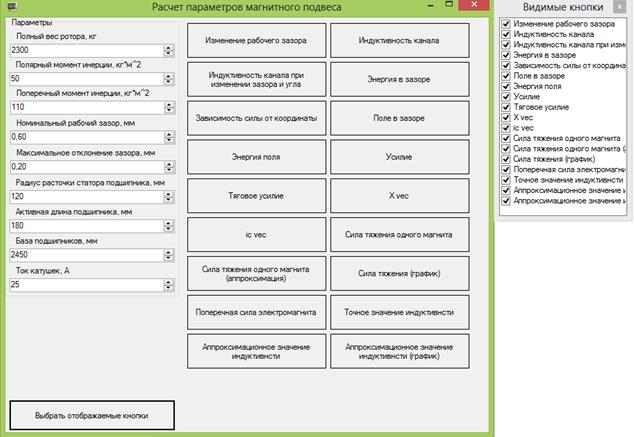
Рис. 5 – основная экранная форма программы
Заключение
Составлены полная и упрощенная математические модели электромагнитных процессов активных магнитных подшипников. Упрощенная модель используется для исследования характеристики тока и генерируемой электромагнитной силы управляемого электромагнита. Полная математическая модель дает возможность осуществить расчет наиболее значимых электромагнитных характеристик радиального активного магнитного подшипника, а именно: расчет изменения рабочего зазора при перемещении ротора, расчет собственной индуктивности канала в зависимости от смещения ротора, расчет энергии магнитного поля в зазоре, расчет тягового усилия АМП, расчет кинетической и потенциальной энергии, расчет электромагнитных сил АМП. Результаты расчета, использующиеся в дальнейшем синтезе системы автоматического управления положением ротора в электромагнитном подвесе, имеют структуру табличной зависимости магнитной силы от тока и текущего положения ротора и зависимости индуктивности от текущего положения.
Рецензенты:
Новиков В. А., д.т.н., профессор кафедры РАПС ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И.Ленина (Ульянова)», г. Санкт –Петербург.
Путов В.В, д.т.н., профессор, декан факультета ЭА ФГБОУ ВПО «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И.Ленина (Ульянова)», г. Санкт-Петербург.
Библиографическая ссылка
Стоцкая А.Д. РАЗРАБОТКА И ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЭЛЕКТРОМАГНИТНЫХ ПРОЦЕССОВ В РАДИАЛЬНЫХ АКТИВНЫХ МАГНИТНЫХ ПОДШИПНИКАХ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10689 (дата обращения: 17.02.2026).



