Нейросетевые методы моделирования сложных экономических систем в последние десятилетия находят все большее применение, благодаря своей универсальности и компьютерной реализованности в различных специализированных пакетах, среди которых можно выделить STATISTICA Neural Networks (SNN). Существенным преимуществом последнего является интеграция с системой статистического анализа STATISTICA различных версий, что позволяет разрабатывать комбинированные технологии, включающие предпрогнозный статистический анализ и моделирование данных, используя широкий набор различных инструментальных средств [3, 4].
Прогнозирование урожайности зерновых культур в условиях Нижнего Поволжья, характеризующееся высоким значением коэффициента вариации (свыше 30%) для основных зерновых культур, ограничивает применение факторных моделей и требует использования методов нелинейной динамики для повышения построения адекватности получаемых моделей. Отмеченная особенность временных рядов урожайности обуславливает методическую погрешность при оценке рисков, связанных с планированием и прогнозированием сельскохозяйственного производства на основе различных методов нелинейной динамики [1 - 3].
Методы нейросетевого моделирования основаны на построении искусственной нейронной сети, моделирующей процессы межгодовых колебаний урожайности, и позволяют описывать динамику моделируемых нелинейные системы.
Основная задача проведенного исследования – повышение достоверности нейросетевого моделирования и, соответственно, прогнозирования уровней ВР урожайности путем предпрогнозного учета внутренних закономерностей динамики изменения урожайности в предшествующие годы на основе использования автокорреляционного анализа многолетних ВР.
Для проведения исследований анализировались ВР различных зерновых культур и зерновых в целом, отобранные по данными Федеральной службы государственной статистики по Волгоградской области (Волгоградстат) за период 1950-2012 гг., фрагмент которых для зерновых в целом представлен в табл.1.
Предварительно проводилась статистическая проверка нулевой гипотезы о соответствии эмпирического закона распределения урожайности нормальному по статистическим критериям (Хи-квадрат Пирсона, Колмогорова-Смирнова).
Для выборочной совокупности урожайности зерновых культур в целом расчетное значение критерия Пирсона составило 51,6, что значительно превышает критическое значение 9,48, определенное по таблице при (α = 0,05; ν = 4).
Таблица 1 – Моделируемая выборочная совокупность урожайностей зерновых в целом по Волгоградской области (1950-2012) годы
|
Годы |
Урожайность, ц/га |
Годы |
Урожайность, ц/га |
Годы |
Урожайность, ц/га |
Годы |
Урожайность, ц/га |
|
1950 |
4,6 |
1970 |
17,5 |
1990 |
20,6 |
2010 |
12,0 |
|
1951 |
4,8 |
1971 |
10,8 |
1991 |
14,4 |
2011 |
17,2 |
|
1952 |
7,5 |
1972 |
4,5 |
1992 |
15,4 |
2012 |
16,4 |
|
1953 |
4,8 |
1973 |
17,2 |
1993 |
20,1 |
|
|
|
1954 |
3,6 |
1974 |
16,0 |
1994 |
12,0 |
|
|
|
1955 |
8,4 |
1975 |
3,8 |
1995 |
5,9 |
|
|
|
1956 |
4,8 |
1976 |
19,2 |
1996 |
8,8 |
|
|
|
1957 |
3,9 |
1977 |
10,2 |
1997 |
14,8 |
|
|
|
1958 |
13,7 |
1978 |
19,7 |
1998 |
4,7 |
|
|
|
1959 |
5,5 |
1979 |
6,8 |
1999 |
7,0 |
|
|
|
1960 |
10,4 |
1980 |
11,9 |
2000 |
12,2 |
|
|
|
1961 |
10,0 |
1981 |
8,2 |
2001 |
17,0 |
|
|
|
1962 |
14,3 |
1982 |
10,2 |
2002 |
16,1 |
|
|
|
1963 |
6,1 |
1983 |
13,1 |
2003 |
15,2 |
|
|
|
1964 |
14,0 |
1984 |
4,1 |
2004 |
19,5 |
|
|
|
1965 |
9,2 |
1985 |
14,1 |
2005 |
18,5 |
|
|
|
1966 |
12,5 |
1986 |
10,6 |
2006 |
17,1 |
|
|
|
1967 |
11,2 |
1987 |
13,2 |
2007 |
13,5 |
|
|
|
1968 |
12,9 |
1988 |
18,5 |
2008 |
24,6 |
|
|
|
1969 |
6,4 |
1989 |
18,4 |
2009 |
19,2 |
|
|
Таким образом, эмпирический закон распределения величин урожайностей для зерновых в целом значимо отличается от нормального по критериям и Пирсона, и Колмогорова–Смирнова. При проведении исследований были выявлены особенности распределения многолетних уровней урожайности и для других групп зерновых культур.
Для обоснования структуры и параметров разрабатываемых математических моделей урожайности основных зерновых культур в засушливых условиях, которые необходимо учитывать при нейросетевом моделировании, и повышения надежности получаемых прогнозов был проведен автокорреляционный анализ исследуемых ВР. Результаты автокорреляционного анализа зерновых в целом представлены на рис. 2.
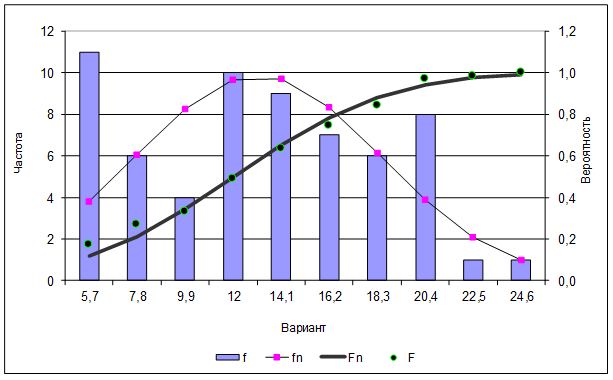
Рисунок 1 – Сопоставление эмпирического распределения зерновых культур в целом с нормальным законом
Анализ полученных автокорреляционных функций ВР урожайности, выполненный для различных групп зерновых культур, показывает их как наличие статистически значимых циклических составляющих, так и различие их характеристик. В соответствии с этим, последующее нейросетевое моделирование ВР урожайностей этих культур должны выполняться с учетом этих статистических характеристик.
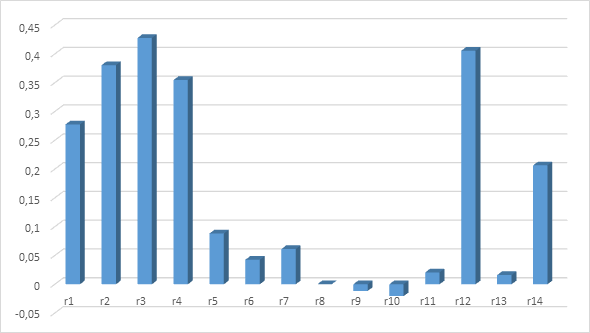
Рисунок 2 – Диаграмма автокорреляционной функции ВР урожайности зерновых культур
На графиках автокорреляционных функций были выявлены статистически значимые пики при одно-, двух-, трех-, четырех- и двенадцатилетнем лагах (рис. 2). Отметим, что наиболее выраженные «пики» наблюдаются при лагах в три и двенадцать лет. Возможной гипотезой для последнего может быть суперпозиция двух- и трехлетних циклов. Таким образом, цикличность ВР урожайности зерновых, подтвержденная в исследованиях за приведенные выше годы, как атрибут эндогенной динамики рассматриваемых экономических систем необходимо учитывать при нелинейном нейросетевом прогнозировании, а также планировании на его основе показателей аграрного производства.
Таким образом, для нейросетевого прогнозирования ВР урожайности можно рекомендовать применение предпрогнозных методов статистического анализа, алгоритмы которых достаточно разработаны. При этом основными задачами являются обоснование численных значений временных параметров нейросети при ее предварительном формировании до обучения.
Практическая реализация разработанных нейросетевых моделей осуществлялась средствами компьютерной математики в среде SNN v4.0. – Интерфейс нейросетевой системы для прогнозирования урожайности зерновых культур на базе SNN v.4 представлен на рисунке 3.
В процессе выбора параметров нейронной сети параметр «Временное окно» (Steps) диалогового окна Сreate Network принимаем равным номеру наиболее выраженного лага на корелограмме (рис.2), т.е. в данном случае равным 3. После этого строим трехслойный персептрон по известным [2, 5] методикам (рис.3).
Выделение обучающей и экзаменующей выборок исходного ВР и обучение создаваемой нейросетевой модели проводилось в частично автоматизированном режиме [3].
Для анализа прогностических характеристик обученной сети использовались различные проекции временного ряда в окне «Time Series Projection», характеризующие количественные и качественные возможности получения прогнозов с различными начальными значениями и горизонтами прогнозирования. Проведенные исследования позволяют рекомендовать полученное семейство нейросетевых моделей для краткосрочного прогнозирования с горизонтом 1-2 года, которое непосредственно можно выполнять в окне «Run Single Case».
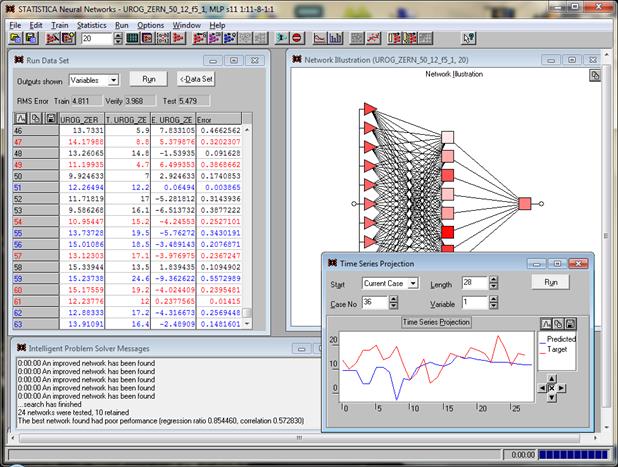
Рисунок 3 – Интерфейс нейросетевой системы для прогнозирования урожайности зерновых культур на базе SNN
Таким образом, предложенная информационная технология нейросетевого моделирования ВР урожайности зерновых культур, основанная на предпрогнозном автокорреляционном анализе многолетних уровней урожайности, позволяет обоснованно выбирать характеристический параметр временного окна «Steps» при построении ИНС, что позволяет снижать погрешность кратко- и среднесрочного прогнозирования урожайности зерновых в засушливых условиях Нижнего Поволжья до 7…12%, что является приемлемым для прогнозирования таких рядов.
Рецензенты:
Терелянский П.В., д.э.н., доцент, зав. Кафедрой ИСЭ, Волгоградский государственный технический университет, г. Волгоград.
Шапров М.Н., д.э.н., профессор, зав. кафедрой Волгоградский государственный аграрный университет, г. Волгоград.
Библиографическая ссылка
Рогачев А.Ф., Шубнов М.Г. ПОСТРОЕНИЕ НЕЙРОСЕТЕВЫХ МОДЕЛЕЙ ПРОГНОЗИРОВАНИЯ ВРЕМЕННЫХ РЯДОВ УРОЖАЙНОСТИ НА ОСНОВЕ АВТОКОРРЕЛЯЦИОННЫХ ФУНКЦИЙ // Современные проблемы науки и образования. 2013. № 5. ;URL: https://science-education.ru/ru/article/view?id=10688 (дата обращения: 02.02.2026).



